Билеты. БИЛЕТЫ. Основные понятия и аксиомы статики
 Скачать 1.03 Mb. Скачать 1.03 Mb.
|
Четвертая теория прочности — энергетическая.Энергетическая теория прочности (теория наибольшей удельной потенциальной энергии формоизменения) исходит из предпосылки о том, что количество потенциальной энергии формоизменения, накопленной к моменту наступления опасного состояния (текучести материала), одинаково как при сложном напряженном состоянии, так и при простом растяжении. Приведенные напряжения при объемном напряженном состоянии: прIV=1 2 ( 1– 2)2+( 2– 3)2+( 3– 1)2 или в частном случае при σy = 0, полагая σx = σ, τxy = τ прIV= 2+3 2 Для частного случая чистого сдвига (σ= 0): прIV= 3 Четвертая теория прочности отображает наступление текучести. Она хорошо подтверждается опытами с пластическими материалами, имеющими одинаковый предел текучести при растяжении и сжатии. Четвертую теорию прочности часто называют теорией октаэдрических касательных напряжений (октаэдрические касательные напряжения в общем случае определяются по формуле окт=1 3 ( 1– 2)2+( 2– 3)2+( 3– 1)2 и к началу развития пластических деформаций при простом растяжении они равны окт=3 2 т ). Устойчивость. Динамическое действие нагрузок. Конструкции при работе нагружаются нс только статическими, но и динамическими нагрузками. Динамическая нагрузка возникает при движснии звеньев механизма с ускорениями. Различают два вида динамических нагрузок: 1) инерционные силы, вызываемые определенными ускорениями звеньев механизма (предполагается, что законы движения звеньев известны); 2) удар, при котором время приложения нагрузки чрезвычайно малое. Задачи по определению напряжений и перемещений с учетом влияния сил инерции решаются на основе метода кинетостатики, позволяющего сводить задачи динамики к задачам статики. Общий метод расчета на динамическую нагрузку основан на известном из теоретической механики принципе Даламбера (метод кинетостатики). Согласно этому принципу, всякое движущееся тело может рассматриваться как находящееся в состоянии мгновенного равновесия, если к действующим на него внешним силам добавить силу инерции, равную произведению массы тела на его ускорение и направленную в сторону, противоположную ускорению. При этом без всяких ограничений можно применять метод сечений, а для определения внутренних усилий использовать уравнения равновесия. В тех же случаях, когда определение сил инерции затруднительно, как, например при ударе, для определения динамических напряжений и деформаций используется закон сохранения энергии. Во всех случаях, где приложена динамическая нагрузка, возникают дополнительные силы, действующие на элемент конструкции, - силы инерции, которые могут быть очень велики; так, например, при подъеме груза с ускорением сила инерции может значительно превосходить вес самого груза. Силы инерции вызывают в элементе конструкции дополнительные напряжения, которые при расчете должны быть учтены. Для упрощения расчетов эти дополнительные напряжения условно считают статическими, но вызванными силами инерции. Так, при равноускоренном (ускорение а, м/с2) движении подъем груза G на стальном тросе (объемный вес у, кг/м3) поперечного сечения А (рис. 9.1) величина динамического напряжения определяется из условия равновесия отсеченной нижней части каната (рис. 9.1, а, б): 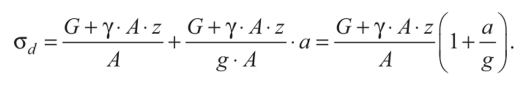 G + yAz Величина -—- является статическим напряжением Gst в сечении троса с учетом его собственного веса у • А • z, поэтому можно записать где Kd = 1 + а/g - динамический коэффициент. 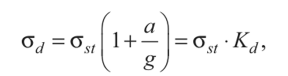 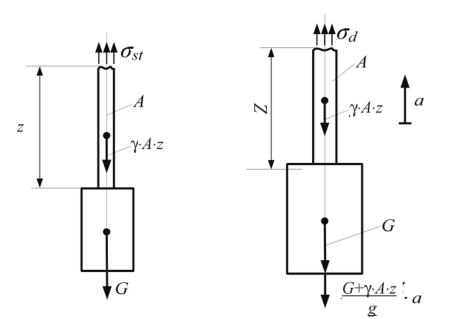 Рис. 9.1. Подъем груза G на стальном тросе Условия прочности при динамической нагрузке откуда  При равномерном прямолинейном движении напряжение в сечении троса будет таким же, как и в случае неподвижного состояния груза. Под ударом понимается механический процесс, быстро протекающий во времени, продолжительность которого меньше периода наиболее медленных собственных колебаний. Удар может быть продольным (растягивающим или сжимающим), когда груз падает на элемент конструкции вдоль его оси, и поперечным (изгибающим), если падение груза на элемент конструкции происходит перпендикулярно к его оси. В общем случае при падении груза на неподвижное тело передается очень большое ускорение, благодаря которому возникает значительная сила инерции. Для приближенного закона сохранения энергии применяются следующие допущения: 1) напряжения при ударе не превосходят предела пропорциональности (закон Гука сохраняет свою силу); 2) удар считается неупругим, т.е. ударяющее тело не отскакивает после удара, а продолжает перемещаться вместе с ударяемым телом как одно целое; 3) масса ударяемого тела считается весьма малой по сравнению с массой ударяющего тела и в расчетах не принимается; 4) потерей части энергии, перешедшей в теплоту и в энергию колебательного движения соударяющихся тел, пренебрегают. Прираниваем работу падающего груза потенциальной энергии деформации ударяемой конструкции. Работа, совершаемая весом G падающего тела с высоты h на произвольную конструкцию, и равна где fd - перемещение в точке удара в результате деформации конструкции. Полученная работа переходит в потенциальную энергию деформации ударяемой конструкции. Обозначим перемещение от единичной силы буквой 8, отношение = Gyd выразит собой эквивалентную силу, которая при своем статическом действии вызовет такое же перемещение fd = G d • 8, какое вызвано ударом. Потенциальная энергия деформации 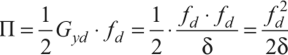 Приравниваем выражения работы и потенциальной энергии: 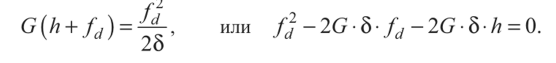 Решив это квадратичное уравнение относительно fd, получим 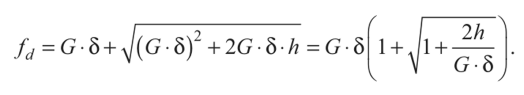 Произведение G • 8 = fst является перемещением от статического действия груза G; следовательно, можно записать 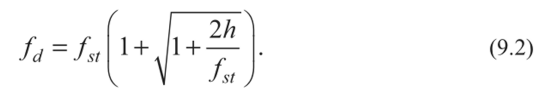 Выражение в скобках показывает, во сколько раз результат ударного (динамического) действия груза больше статического действия, и называется динамическим коэффициентом 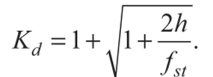 Отсюда видно, что величина Кс/ возрастает с увеличением высоты И падения груза. Формула (9.2) может быть представлена в виде На основании принятого допущения о справедливости закона Гука в пределах упругости можно записать 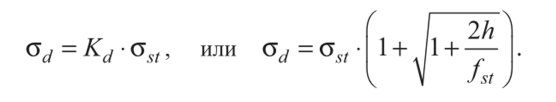 Если высота падения груза h — О, т.е. нагрузку приложить сразу (внезапное действие нагрузки), величина динамического коэффициента 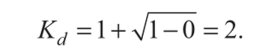 Таким образом, внезапно приложенная нагрузка вызывает вдвое большие напряжение и деформации, чем при статическом действии той же нагрузки. Пример 9.1. Груз весом G — 50 кН поднимается краном с ускорением а = 4,9 м/с2. Определить динамическое напряжение в тросе, если его длина / = 12 м, площадь поперечного сечения А = 0,0006 м2, объемный вес 7 = 0,078 МН/м3 (0,0078 кГ/см3). Решение Величина динамического напряжения 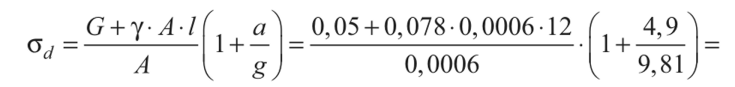 Устойчивость равновесия сжатых стержней. Формула Эйлера. 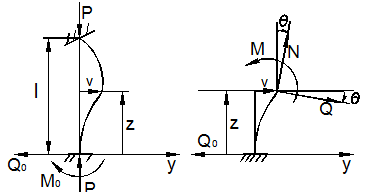 Считаем стержень идеально прямым и сжатым центрально приложенными силамиP (рис. 9.15,а). Следуя методу Эйлера, будем считать исходное состояние равновесия упругого стержня устойчивым, если после статического приложения и снятия возмущающей силы при постоянных внешних сжимающих силах P стержень возвращается к своей исходной прямолинейной форме равновесия. В противном случае состояние равновесия считаем неустойчивым. Допустим, что стержень остался в изогнутом состоянии (рис. 9.15,б). Отсечём часть стержня на расстоянии z от начала координат, считая угол поворота сечения малой величиной, и составим уравнения равновесия: Изгибающий момент в поперечном сечении, согласно (6.9), равен: Приравнивая выражения моментов (9.20), (9.21), находим: Дифференцируя (9.22) по z, получим: дифференцируя (9.23) по z, приходим к уравнению изогнутой оси потерявшего устойчивость стержня четвёртого порядка: Введём обозначение: Тогда уравнения (9.22), (9.24) можно записать в виде Общее решение уравнения (9.26) имеет вид: В него входят четыре произвольные постоянные Общее решение уравнения (9.27): В него входят четыре произвольные постоянные Производные: 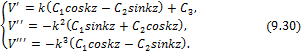 Используя (9.30), из (9.21), (9.23) находим: Постоянные находятся из граничных условий. Для шарнирно закреплённого по концам стержня при z=0 и z=l имеем условия: Для стержня, защемлённого при z=0 и свободного от закрепления при z=l, должны выполняться условия: при z=0, Если на незакреплённом конце при z=l действуют внешние моментm и поперечная силаR, то M=m, Q=R. При любом закреплении концов стержня мы имеем четыре граничных условия (по два на каждом краю), которые при подстановке в них выражений (9.28), (9.29) приводят к системе четырёх однородных алгебраических уравнений вида: или 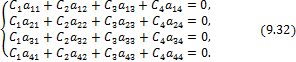 Система уравнений (9.32) имеет отличные от нуля решения только при условии, что её определитель: 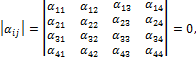 откуда, после его раскрытия, находим некоторое числовое значение kl: где - некоторое число. Возводя обе части полученного равенства в квадрат и используя обозначение (9.25), получаем формулу для критического значения силы (нагрузки бифуркации) Эйлера: где - приведённая длина стержня, - коэффициент приведения длины стержня к длине шарнирно опёртого по концам стержня. Можно сказать, что – число, показывающее, во сколько следует увеличить длину шарнирно-опертого стержня, чтобы критическая сила для него равнялась критической силе стержня длиной в рассматриваемых условиях закрепления. Понятие о приведенной длине было впервые введено профессором Петербургского института инженеров путей сообщения Ф. Ясинским. Соответствующее критическое напряжение Эйлера: где гибкость стержня, - радиус инерции площади поперечного сечения. Формула (9.33) для критической силы сжатой колонны была получена Эйлером в 1744г. а для сжатого шарнирно опёртого стержня - в 1757г. Во времена Эйлера (1707 – 1783) главными конструкционными материалами были камень и древесина. Их слабое сопротивление нагрузкам заставляло инженеров создавать массивные конструкции и сооружения, для которых вопросы устойчивости не имели первостепенного значения. Поэтому теория устойчивости Эйлера долгое время не находила практического применения. Только с введением стали в проектирование инженерных конструкций с гибкими элементами, вопросы устойчивости получили большое практическое значение. Основные положения детали машин. Понятия о надежности машин. Машиной называют устройство, выполняющее механические движения для преобразования энергии, материалов, движения или для накопления и переработки информации с целью повышения производительности, замены или облегчения физического и умственного труда человека. Машины делят в основном на две большие группы: машины-двигатели и рабочие машины. Машины-двигатели – энергетические машины, предназначенные для преобразования энергии любого вида в энергию движения исполнительных органов рабочих машин. К таким машинам относят электродвигатели, двигатели внутреннего сгорания, паровые машины и т.д. Рабочие машины предназначены для облегчения и замены физического труда человека по изменению формы, свойств, состояния, размера и положения обрабатываемых материалов, для перемещения различных грузов, а также для облегчения и замены его логической деятельности при выполнении расчетных операций и операций контроля и управления производственными процессами. К таким машинам относят всевозможные станки для обработки материалов, дорожные, сельскохозяйственные и транспортные машины, подъемные краны, транспортеры, вычислительные машины, устройства робототехники: манипуляторы, автооператоры, промышленные роботы и др. В зависимости от способа управления движением машин различают: машины ручного управления, полуавтоматического и автоматического действия. Многочисленные разновидности машин отличаются осуществляемыми с их помощью производственными процессами. Их сходство определяется наличием в машинах механизмов, предназначенных для передачи и преобразования движения. Механизмом называют совокупность взаимосвязанных звеньев, допускающую их относительное движение и предназначенную для преобразования движения одного или нескольких звеньев в требуемые движения остальных звеньев. Звено механизма – одна или несколько жестко соединенных деталей. Различают входные и выходные звенья механизма. Входное звено – звено, которому сообщается движение, преобразуемое механизмом в требуемые движения других звеньев. Выходное звено – звено, совершающее движение, для выполнения которого предназначен механизм. В каждой паре совместно работающих звеньев в направлении силового потока различают ведущие и ведомые звенья. Соединение двух соприкасающихся звеньев, допускающих относительное движение, называют кинематической парой, например винт и гайка, зубчатая передача, шарнир и т.д. По функциональному признаку кинема- тические пары могут быть вращательными, поступательными, винтовыми и т.д. Все машины и механизмы состоят из деталей и узлов. Деталь – изделие, изготовленное из однородного по наименованию и марке материала без применения сборочных операций. Детали могут быть простыми (шпонка, болт, гайка и т.д.) или сложными (корпус редуктора, станина станка, коленчатый вал и т.д.). Детали (частично или полностью) объединяют в узлы. Узел представляет собой законченную сборочную единицу, состоящую из ряда деталей, имеющих общее функциональное назначение (подшипник качения, муфта, редуктор и т.д.). Анализируя конструкции различных машин, их узлов и деталей, не трудно заметить, что многие типы деталей и узлов встречаются почти во всех машинах с одними и теми же функциональными назначениями, например болты, валы, механические передачи, подшипники, муфты и др. Эти детали (узлы) называют деталями общего назначения; их теорию, расчет и конструирование изучают в курсе «Детали машин». Все другие детали (узлы), применяющиеся только в одном или нескольких типах машин (шпиндели станков, коленчатые валы, поршни, шатуны, канаты и т.п.), относят к деталям специального назначения и изучают в соответствующих специальных курсах. Детали общего назначения применяют в машиностроении в очень больших количествах (в одном автомобиле более пяти тысяч деталей, в самолете – более миллиона, в стране ежегодно изготовляют миллионы зубчатых колес), поэтому любое усовершенствование методов расчета, правил и норм конструирования этих деталей позволяет уменьшить затраты материала, повысить долговечность, дает большой экономический эффект. Все детали и узлы общего назначения делят на три основные группы: соединительные детали и соединения (сварные, резьбовые, шпоночные и др.); передачи вращательного движения (ременные, зубчатые, червячные и др.); детали и узлы, обслуживающие передачи (валы, подшипники, муфты и др.). |
