|
|
Билеты. БИЛЕТЫ. Основные понятия и аксиомы статики
Понятия о напряжениях и деформациях.
Вектором полного напряжения в точке К в сечении S называют величину
(8.1)
где - элементарная площадка в окрестности точки K;
- равнодействующая внутренних сил на площадке.
Напряжение есть внутренняя сила, приходящаяся на единицу площади (в паскалях). Полное напряжение р раскладывают на составляющие: по нормали к сечению (нормальное напряжение ) и по двум осям в плоскости сечения (касательные напряжения ). Если через т. К провести другое сечение, напряжение будет, вообще говоря, другим. Совокупность напряжений для всего множества площадок, проходящих через точку, образует напряженное состояние в точке.
Под действием внешних сил все тела деформируются. Это существенно влияет на распределение в теле внутренних сил, хотя деформации, как правило, незначительны. При деформировании точки тела меняют свое положение в пространстве. Вектор, имеющий начало в точке недеформированного тела, а конец в той же точке деформированного тела, называют вектором линейного перемещения точки. Вводят также понятие углового перемещения. Если рассмотреть отрезок прямой между двумя близкими точками до и после деформирования, то он поворачивается на некоторый угол.
Если на систему наложены связи, достаточные для того, чтобы исключить ее перемещение в пространстве как жесткого целого, то систему называют кинематически неизменяемой. Именно такие системы и рассматриваются, как правило, в СМ. В противном случае рассматривается только часть перемещений, обусловленная деформациями. Тогда для большинства систем перемещения любой точки являются малыми по сравнению с размерами тела. Поэтому согласно принципу начальных размеров при составлении уравнений статики не учитывают изменение размеров (есть исключения).
Чтобы характеризовать интенсивность изменения размеров и формы тела, рассмотрим тело до и после деформирования. Величину
(8.2)
называют линейной деформацией или просто деформацией в точке А по направлению АВ (порядок 10-3). В той же точке в другом направлении деформация, вообще говоря, будет другой. В направлении осей х, у и z имеем х, у и z.
Рассмотрим прямой угол, образованный в теле двумя отрезками OD и ОС . После нагружения тела внешними силами этот угол изменится и примет значение C'O'D'. Величину
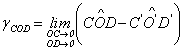 (8.3) (8.3)
называют угловой деформацией или углом сдвига в точке О в плоскости COD.
В координатных плоскостях углы сдвига обозначают через уz,zxи ху.
Принцип независимости сил.
Во многих случаях перемещения в определенных пределах пропорциональны действующим силам (Гук, 1660 г.). Коэффициент пропорциональности зависит как от физических свойств материала, так и от геометрии системы. В современной трактовке закон Гука определяет линейную зависимость между напряжением и деформацией, и тогда коэффициенты пропорциональности являются константами материала. Эта зависимость сохраняется как при возрастании, так и при убывании сил и отражает упругие свойства системы.
Можно доказать, что системы, для которых выполняется закон Гука, подчиняются принципу суперпозиции (принципу независимости действия сил): перемещения и внутренние силы в упругом теле, не зависят от порядка приложения внешних сил. Если к системе приложено несколько сил, то можно определить внутренние силы, напряжения, перемещения и деформации от каждой силы в отдельности, а затем результат действия всех сил получить как сумму действий от каждой силы.
При решении задач СМ используется принцип Сен-Венана. Предполагается, что если к телу приложена самоуравновешивающаяся система сил, то напряжения и деформации быстро убывают при удалении от места приложения нагрузки. Согласно этому принципу способ приложения нагрузки влияет только на деформацию тела в малом объеме, примыкающем к месту приложения нагрузки, и не влияет на деформацию тела вдали от точек ее приложения.
Диаграмма растяжения и сжатия.
Диаграммы растяжения
Д ля изучения свойств материалов и установления значений предельных напряжений проводят испытания образцов материала вплоть до разрушения. Эксперимент ведут в стандартных условиях на специальных машинах. Наиболее распространены испытания на растяжение статической нагрузкой, т.к. они наиболее просты и дают возможность судить о поведении материала при других видах деформации. ля изучения свойств материалов и установления значений предельных напряжений проводят испытания образцов материала вплоть до разрушения. Эксперимент ведут в стандартных условиях на специальных машинах. Наиболее распространены испытания на растяжение статической нагрузкой, т.к. они наиболее просты и дают возможность судить о поведении материала при других видах деформации.
Д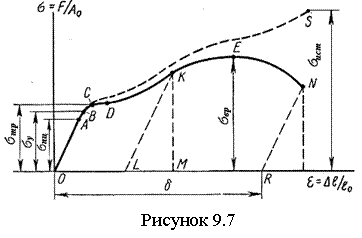 ля испытаний применяют цилиндрические (см. рисунок 9.6) или плоские образцы. Обычно d0=20 мм, l0=10d0 или l0=5d0. При испытании записывается диаграмма зависимости между F и Δl. Для возможности сравнения результатов по образцам различных размеров, диаграмму F-Δl рассматривают и как диаграмму σ-ε. Это не совсем верно, поскольку подразумевается, что σ=F/A0и ε=∆l/l0 (A0, l0 –первоначальная площадь поперечного сечения образца и первоначальная длина образца). Т.к. истинные σ и ε должны определяться через текущие значения A иl, то такую диаграмму в координатах σ и ε называют условной диаграммой растяжения. ля испытаний применяют цилиндрические (см. рисунок 9.6) или плоские образцы. Обычно d0=20 мм, l0=10d0 или l0=5d0. При испытании записывается диаграмма зависимости между F и Δl. Для возможности сравнения результатов по образцам различных размеров, диаграмму F-Δl рассматривают и как диаграмму σ-ε. Это не совсем верно, поскольку подразумевается, что σ=F/A0и ε=∆l/l0 (A0, l0 –первоначальная площадь поперечного сечения образца и первоначальная длина образца). Т.к. истинные σ и ε должны определяться через текущие значения A иl, то такую диаграмму в координатах σ и ε называют условной диаграммой растяжения.
На рисунке 9.7 сплошной линией показана условная диаграмма растяжения малоуглеродистой стали. На участке ОА до некоторого напряжения σпц, называемого пределом пропорциональности, ε растет пропорционально σ, т.е. выполняется закон Гука (для стали Ст3 σпц≈ 200 МПа). Дальше диаграмма становится криволинейной, до величины σу, называемой пределом упругости, материал еще сохраняет упругие свойства. Значения σпц и σу близки (для Ст3 σу≈ 210 МПа), на практике их не различают.
При дальнейшем увеличении нагрузки наступает момент (т.С), когда деформации начинают расти без увеличения нагрузки. Горизонтальный участок СD называется площадкой текучести, соответствующее напряжение - пределом текучести при растяжении σтр (240…400 МПа для Ст3).
Далее диаграмма поднимается вверх. В т.Е достигается наибольшее условное напряжение, называемое пределом прочности или временным сопротивлением σвр (для Ст3 σвр=400…500 МПа). На образце появляется резкое местное сужение, т.н. шейка. Площадь сечения образца в шейке быстро уменьшается и, как следствие, падает усилие и σ. Разрыв образца происходит по наименьшему сечению. Предел прочности не есть напряжение, при котором происходит разрушение образца. Если относить растягивающую силу не к A0, а к площади шейки, то в т.S в шейке перед разрывом σист > σвр.
При испытании определяют также относительное остаточное удлинение при разрыве δ, являющееся характеристикой пластичности материала,
(9.17)
где l0 – первоначальная расчетная длина образца;
l1 – расчетная длина образца после разрыва.
Для Ст3 δ ≥24%, у высокопрочных сталей δ=(7…10)%. Это удлинение является усредненным, истинное удлинение возникает в месте разрыва.
Для изучения значительных пластических деформаций необходимо знать истинную диаграмму растяжения (кривая OCS на рисунке 9.7).
Р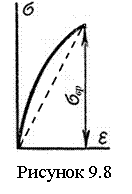 ассмотренная диаграмма растяжения является характерной для т.н. пластичных материалов. К весьма пластичным материалам относятся медь, алюминий, латунь, малоуглеродистая сталь и др., к менее пластичным - дуралюмин и бронза, к слабо пластичным – большинство легированных сталей. Ряд пластичных материалов при растяжении дает диаграмму без площадки текучести; для них устанавливается т.н. условный предел текучести – это напряжение, которому соответствует определенная величина остаточной деформации. Условному пределу текучести σ0,2 соответствует остаточная деформация 0,2%. ассмотренная диаграмма растяжения является характерной для т.н. пластичных материалов. К весьма пластичным материалам относятся медь, алюминий, латунь, малоуглеродистая сталь и др., к менее пластичным - дуралюмин и бронза, к слабо пластичным – большинство легированных сталей. Ряд пластичных материалов при растяжении дает диаграмму без площадки текучести; для них устанавливается т.н. условный предел текучести – это напряжение, которому соответствует определенная величина остаточной деформации. Условному пределу текучести σ0,2 соответствует остаточная деформация 0,2%.
Противоположным свойству пластичности является хрупкость. К хрупким материалам (δ < 2-5%) относятся чугун, инструментальная сталь, камень, бетон, стекло и др.
Диаграмма растяжения образцов из хрупких материалов (рисунок 9.8) имеет ряд особенностей. Здесь отклонение от закона Гука начинается очень рано. Разрыв наступает внезапно при очень малых деформациях, без шейки. При испытании определяют только предел прочности σвр. При расчетах отклонение от закона Гука для хрупких материалов не учитывают, заменяя криволинейную диаграмму прямолинейной. Заметное влияние на σвр оказывают размеры образца, что оценивают масштабным коэффициентом.
Диаграммы сжатия
Используют образцы в форме кубиков или невысоких цилиндров (h≤ 3d) - иначе возникает изгиб. Применение очень коротких образцов также нежелательно, т.к. силы трения на торцах искажают картину. Вид диаграммы сжатия хрупких материалов такой же, как диаграммы растяжения. По диаграмме определяют σвс и δ, при этом σвс обычно больше σвр.
Н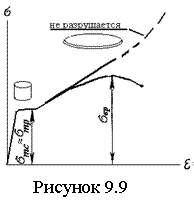 а рисунке 9.9 показана типичная диаграмма сжатия пластичного материала. Вначале она идет так же, как и диаграмма растяжения, а затем вверх – образец сплющивается и не разрушается. Пределы текучести при растяжении и сжатии для малоуглеродистых сталей практически одинаковы. а рисунке 9.9 показана типичная диаграмма сжатия пластичного материала. Вначале она идет так же, как и диаграмма растяжения, а затем вверх – образец сплющивается и не разрушается. Пределы текучести при растяжении и сжатии для малоуглеродистых сталей практически одинаковы.
Сдвиг и кручение.
Ч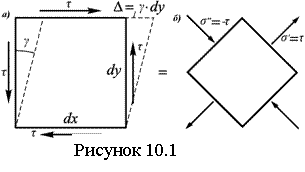 истый сдвиг (ЧС) – это напряженное состояние, при котором на гранях выделенного из тела элемента возникают только касательные напряжения (см. рисунок 10.1,а). Однородный ЧС имеет место при кручении тонкостенной трубки. истый сдвиг (ЧС) – это напряженное состояние, при котором на гранях выделенного из тела элемента возникают только касательные напряжения (см. рисунок 10.1,а). Однородный ЧС имеет место при кручении тонкостенной трубки.
Можно доказать, что если из элемента, находящегося в условиях ЧС, вырезать элемент с гранями, наклоненными под углами в 45º к исходным граням, то на них касательных напряжений не будет, а будут иметь место только нормальные напряжения (см. рисунок 10.1,б), на одной паре противоположных граней напряжения - растягивающие (σ’=), на другой – сжимающие (σ”=).
Напряжения связаны с угловой деформацией γ законом Гука
=G∙γ. (10.1)
Испытания на ЧС тонкостенной трубки, закручиваемой моментами, дают условную диаграмму сдвига в координатах и γ, которая сходна с диаграммой растяжения, при этом для пластичных металлов т=(0,5…0,55)σт.
Напряженное состояние, близкое к ЧС, возникает в заклепках, болтах (устанавливаемых без зазора), шпонках, шлицах, сварных швах.
Под кручением понимается такой вид нагружения стержня, при котором в его поперечных сечениях возникает только крутящий момент Мкр. Кручение обычно возникает при нагружении стержня парами сил (скручивающими моментами), плоскости действия которых перпендикулярны продольной оси стержня. Эпюру крутящего момента строят с использованием метода сечений, при этом Мкр равен сумме моментов относительно продольной оси стержня всех пар сил, расположенных по одну сторону от рассматриваемого сечения
Мкр = ∑Mi. (10.2)
Правило знаков: если наблюдатель со стороны внешней нормали к сечению видит момент Мкр направленным против часовой стрелки, то он считается положительным, иначе - отрицательным. Внешние моменты в (10.2) должны браться с противоположным правилом.
При расчете стержня (вала) обычно требуется определить напряжения и угловые перемещения в зависимости от величин внешних моментов. Методами СМ можно получить решение только для стрежня кругового или кольцевого поперечного сечения (будем рассматривать только этот случай) и для тонкостенных стержней. В случае кручения стержня с круговым поперечным сечением каждое сечение стержня поворачивается в своей плоскости на некоторый угол как жесткое целое (гипотеза плоских сечений).
Р ассмотрим стержень с круговым поперечным сечением, показанный на рисунке 10.2,а. В его поперечных сечениях возникает постоянный крутящий момент Мкр=M. Двумя поперечными сечениями, выделим из стержня элемент длиной dz, а из него свою очередь двумя цилиндрическими поверхностями с радиусами и (+d) – элементарное кольцо, показанное на рисунке 10.2,в. В результате кручения правое торцевое сечение кольца повернется на угол d. Тогда ассмотрим стержень с круговым поперечным сечением, показанный на рисунке 10.2,а. В его поперечных сечениях возникает постоянный крутящий момент Мкр=M. Двумя поперечными сечениями, выделим из стержня элемент длиной dz, а из него свою очередь двумя цилиндрическими поверхностями с радиусами и (+d) – элементарное кольцо, показанное на рисунке 10.2,в. В результате кручения правое торцевое сечение кольца повернется на угол d. Тогда
. (10.3)
Угол представляет собой угол сдвига цилиндрической поверхности под действием касательных напряжений . Величину
(10.4)
называют относительным углом закручивания. Это угол взаимного поворота двух сечений, отнесенный к расстоянию между ними.
Из рассмотрения (10.3) и (10.4) получим = ∙θ. (10.5)
Чистый сдвиг. Закон Гука при сдвиге.
Чистым сдвигом называется такой вид напряженного состояния, при котором на гранях элемента действуют только касательные напряжения, как на рис. 4.10. Здесь а — абсолютный сдвиг, угол у — угол сдвига. Так как в пределах упругой деформации угол сдвига очень мал, то можно записать tgy -а/h
у, а угол у — назвать относительным сдвигом.
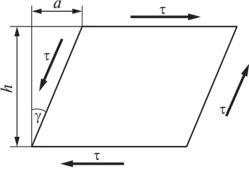
Рис. 4.10. Напряжения и деформации элемента при сдвиге
Закон Гука при сдвиге имеет вид
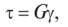
где у — угол сдвига, или угловая деформация; G — модуль сдвига (модуль упругости второго рода), характеризующий способность материала сопротивляться деформации сдвига.
В реальных конструкциях довольно сложно реализовать чистый сдвиг, однако существует целый ряд конструкций (сварные, заклепочные соединения и др.), в которых нормальные напряжения в сечениях намного меньше касательных напряжений. Такие детали рассчитывают на чистый сдвиг (срез) для предварительного определения их размеров.
Условие прочности в этом случае имеет вид
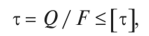
где Q—поперечная сила; F— площадь поперечного сечения; [т] — допускаемое касательное напряжение.
Кручением называется такой вид деформации, при котором в поперечных сечениях действует только крутящий момент, а остальные силовые факторы отсутствуют.
Вращающиеся и работающие на кручение стержни называются валами.
Для определения значений крутящих моментов по длине вала строится эпюра крутящих моментов. Знак «плюс» у крутящего момента выбирается в том случае, если наблюдатель смотрит на поперечное сечение со стороны внешней нормали и видит момент направленным по часовой стрелке. В противном случае момент считается отрицательным.
При кручении стержня происходит поворот одного сечения относительно другого на некоторый угол ср, называемый углом закручивания (рис. 4.11).
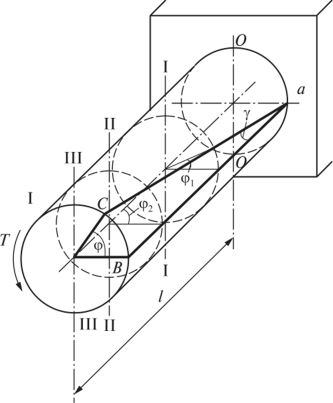
Р и с. 4.11. Схема деформации вала при кручении
Относительным углом закручивания называется отношение угла закручивания на единицу длины стержня
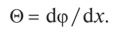
Тогда
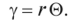
На основании закона Гука определим касательное напряжение
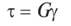
или

Используя (4.4), можно найти напряжение по относительному сдвигу в окрестности любой точки тела, находящейся на расстоянии р от оси (рис. 4.12, а)

Из (4.5) следует, что касательные напряжения в точках сечения пропорциональны расстоянию его от оси. Максимальные касательные напряжения действуют вблизи наружной поверхности вала (рис. 4.12, в).
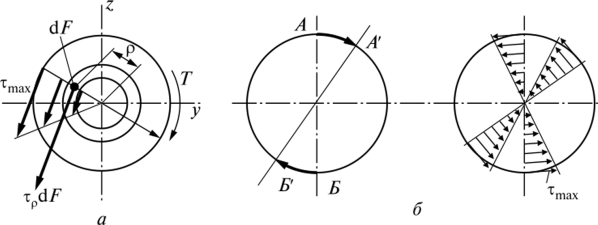
Рис. 4.12. Касательные напряжения и деформации при кручении: а — напряжение в некоторой точке сечения; б — поворот сечений при кручении; в — эпюра касательных напряжений по сечению
Найдем зависимость между 0 и крутящим моментом Т. Для этого в произвольной точке сечения выделим элементарную площадку dF, на которой будет действовать элементарная окружная сила Tpd/7. Определим элементарный момент, создаваемый этой силой, относительно оси стержня
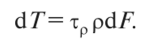
Суммируя элементарные площадки, получим 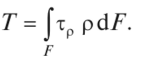 С учетом (4.5) С учетом (4.5)
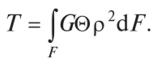
Так как G0 = const, то 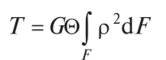 или или

где Iр = J p2d/7 — полярный момент инерции стержня, чисто геомет-
F
рическая характеристика.
Относительный угол закручивания

Произведение GIP называется жесткостью сечения стержня при кручении.
Подставим в (4.6) значение 0 из равенства (4.7)

Из (4.8) получим наибольшее касательное напряжение
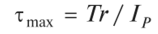
или
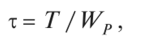
где WP = Ip/r — полярный момент сопротивления или момент сопротивления при кручении (геометрическая характеристика); WP= 0,2 d3 — для круглого сплошного сечения; WP=0,2 ЕР( 1 — с4), с = d/D — для кольцевого сечения.
Запишем условие прочности при кручении:
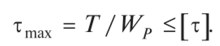
При известном значении крутящего момента в сечении и заданном материале вала можно подобрать диаметр вала сплошного сечения:

На работоспособность элементов конструкций существенное влияние оказывает их жесткость — способность сопротивляться деформированию. Для валов ее оценивают путем сопоставления расчетных относительных углов закручивания и допускаемых:
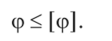
Условие жесткости вала имеет вид  где / — длина вала. где / — длина вала.
|
|
|
 Скачать 1.03 Mb.
Скачать 1.03 Mb.