|
|
Билеты. БИЛЕТЫ. Основные понятия и аксиомы статики
Основные понятия и аксиомы статики.
Наука об общих законах движения и равновесия материальных тел и о возникающих при этом взаимодействиях между телами называется теоретической механикой.
Статикой называется раздел механики, в котором излагается общее учение о силах и изучается условия равновесия материальных тел, находящихся под действием сил.
Объектами изучения ТМ являются модели материальных тел, а именно, материальная точка (МТ), система МТ и абсолютно твердое тело (АТТ).
МТ называют тело, размерами которого можно пренебречь, считая, что масса сосредоточена в точке. Системой МТ называют совокупность МТ, положения и движения которых взаимосвязаны между собой. АТТ называют тело, в котором расстояния между любыми точками остаются неизменными. Все реальные тела в результате воздействий в определенной мере изменяют свои размеры и форму (деформируются). Эти деформации зачастую малы, и при решении ряда задач ими можно пренебречь, считая тело абсолютно твердым.
Состояние равновесия или движения тела зависит от характера его взаимодействий с другими телами, мерой которых является сила. Сила - вектор, характеризующийся численной величиной, направлением и точкой приложения; графически изображается направленным отрезком прямой. Прямую, вдоль которой направлена сила, называют ее линией действия (ЛД). Силу будем обозначать, например, как , тогда F= - ее модуль. Система сил – это совокупность сил, действующих на объект; обозначаем .
Если систему сил (СС), действующих на тело, можно заменить другой СС, не изменяя при этом состояния покоя или движения тела, то эти СС называют эквивалентными, . Если данной СС эквивалентна одна сила, то эта сила называется равнодействующей для этой СС. Если обозначить ее как *, то *
. Не каждая СС имеет равнодействующую. СС называют уравновешенной, если она, будучи приложенной к телу, не изменяет его состояния покоя или движения. Действие уравновешенной СС эквивалентно нулю, т.е.
0. Силой, уравновешивающей СС, называют силу, которая, будучи присоединенной к этой СС, составит вместе с ней новую СС, эквивалентную нулю. Сила, приложенная к телу в одной точке, называется сосредоточенной.
В основе статики лежат 6 аксиом, рассматриваемых ниже.
1. Для равновесия 2 сил, приложенных к телу, необходимо и достаточно, чтобы силы были равны по величине и направлены в противоположные стороны вдоль прямой, соединяющей их точки приложения: F1 = F2, .
2. Не изменяя действия системы сил на твердое тело, можно к этой системе прибавить или отнять от нее уравновешенную СС. Следствие: не изменяя действия силы на АТТ, ее можно переносить в любую точку тела вдоль ее ЛД.
3. Равнодействующая двух сил, приложенных в одной точке, определяется диагональю параллелограмма, построенного на силах, т.е. .
4. Силы взаимодействия двух тел равны по величине и направлены вдоль одной прямой в противоположные стороны: F21 = F12, .
5. Несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их действие реакциями.
6. Равновесие деформируемого тела, находящегося под действием данной СС, не нарушится, если считать его затвердевшим (абсолютно твердым).
Система сходящихся сил.
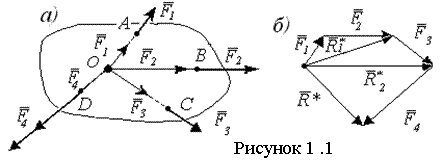
Различают следующие типы систем сил (СС): система сходящихся сил, система параллельных сил, произвольная СС. СС сил называется: сходящейся, если линии действия (ЛД) всех сил системы пересекаются в одной точке; параллельной, если ЛД сил параллельны между собой; произвольной - если ЛД сил не параллельны и не пересекаются в одной точке. Все указанные СС могут быть плоскими или пространственными. СС называется плоской, если ЛД всех сил лежат в одной плоскости; в противном случае СС - пространственная.
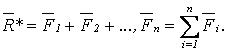 (1.1) (1.1)
Равнодействующая соединяет начало первого вектора с концом последнего. Т.е., равнодействующая системы сходящихся сил (ССС) равна векторной сумме сил, входящих в систему, и ее ЛД проходит через точку пересечения ЛД слагаемых сил. Чтобы найти равнодействующую геометрическим способом, надо построить в точке пересечения их ЛД силовой многоугольник на слагаемых силах; замыкающая силового многоугольника будет равнодействующей.
Аналитический способ определения равнодействующей ССС.
, , . (1.2)
Модуль равнодействующей силы и направление определяются, как
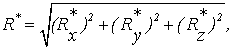 (1.3) (1.3)
, , . (1.4)
Для равновесия ССС необходимо и достаточно, чтобы или (условия равновесия в векторном виде). В геометрическом смысле: силовой многоугольник должен быть замкнут. В аналитическом виде: должны равняться нулю суммы проекций на три оси всех сил, входящих в систему,
, , . (1.5)
Для плоской ССС: , . (1.6)
Произвольная плоская система сил.
Произвольной плоской системой сил называется совокупность сил, линии действия которых находятся в одной плоскости.
Если все силы, действующие на твердое тело, лежат на одной плоскости, выберем систему координат xOy в плоскости действия сил (рисунок 2.1). В этом случае обнаружим, что
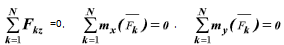
Далее, вспомнив определение момента силы относительно оси, замечаем, что сумма моментов всех сил относительно оси z равна алгебраической сумме моментов этих сил относительно начала координат, т.е. точки О.
В результате останутся следующие три аналитические условия равновесия:
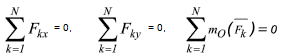
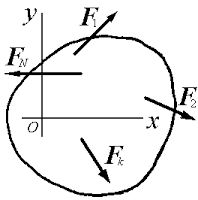
Рисунок 2.1
Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из координатных осей x и y и сумма моментов всех сил относительно любой точки, лежащих в плоскости действия сил, были равны нулю.
Главным вектором системы сил называется вектор, равный векторной сумме этих сил:
R = ΣFk (1.1)
Главным моментом системы сил относительно точки O тела, называется вектор, равный векторной сумме моментов всех сил системы относительно этой точки:
MO = ΣMO(Fk) (1.2)
Пара сил.
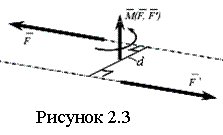
Парой сил, приложенной к АТТ, называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны и не лежащих на одной прямой (см. рисунок 2.3). Сумма сил пары равна нулю, но пара сил не уравновешена. Кратчайшее расстояние между ЛД сил пары называют плечом пары, а плоскость, в которой лежат силы пары - плоскостью действия пары. Совокупность нескольких пар сил, действующих на тело, называется системой пар сил. Пара не приводится к равнодействующей. Действие пары на тело характеризуется векторным моментом пары - это вектор , перпендикулярный плоскости действия пары и направленный в ту сторону, откуда видно, что пара стремится повернуть тело против часовой стрелки, и численно равный произведению модуля одной из сил пары на ее плечо F∙d. Пару сил можно переносить куда угодно в плоскости и в параллельную плоскость, изменяя модуль силы и плечо, но, сохраняя при этом неизменными модуль момента пары и направление, в котором она стремится вращать твердое тело, т.е. векторный момент пары сил есть свободный вектор.
Две пары сил, имеющие одинаковые векторные моменты, эквивалентны независимо от расположения и величин модулей сил и плечей пар.
Если пары расположены в одной плоскости, то моменты пар можно рассматривать как алгебраические величины. Момент пары считают положительным, если пара стремится вращать тело против часовой стрелки. Тогда для плоской системы пар сил
(2.8)
и  . (2.9) . (2.9)
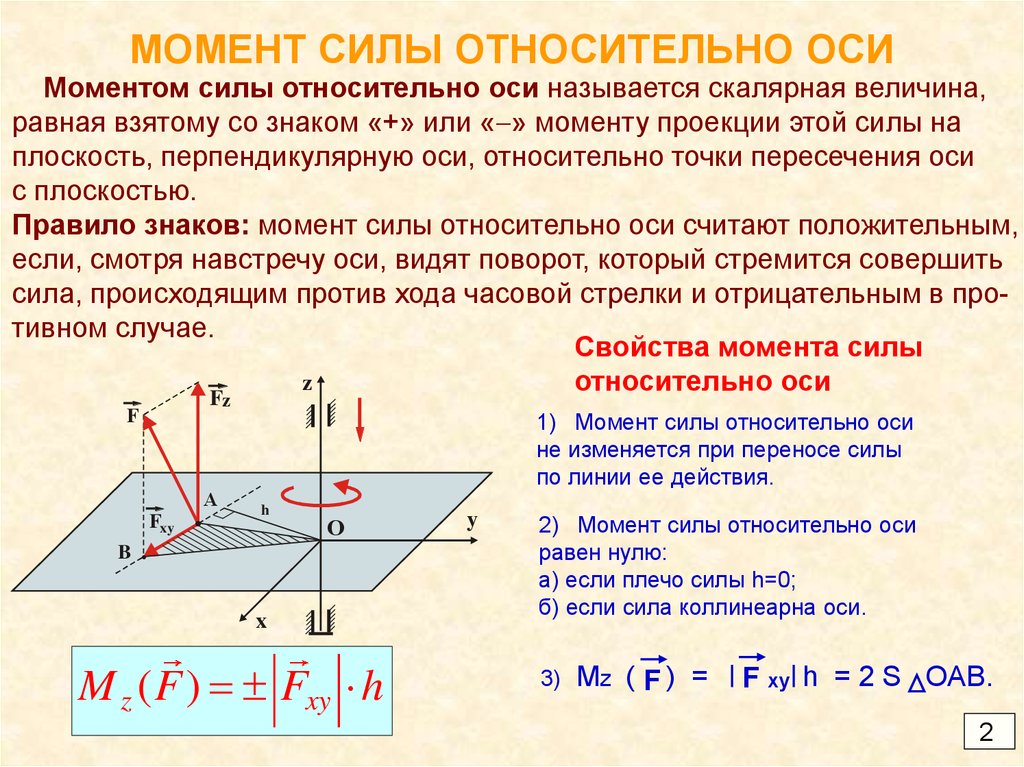
Момент силы относительно оси. Условия равновесия.
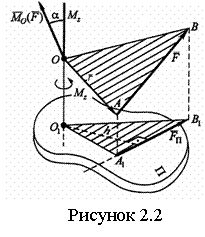
Моментом силы относительно оси называется проекция на эту ось векторного момента силы, взятого относительно любой точки на оси, т. е.
. (2.5)
Иначе: момент силы относительно оси- это алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, взятый относительно точкипересечения оси с плоскостью (см. рисунок 2.2)
. (2.6)
Момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости. Момент силы относительно начала координат равен
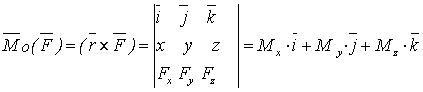 , ,
откуда получим моменты силы относительно осей координат
, , . (2.7)
Теорема о сложении пар сил. Совокупность пар сил, действующих на тело, эквивалентна одной паре с моментом, равным сумме векторных моментов всех пар сил, . Условия равновесия системы пар имеют вид
. (2.10)
Чтобы произвольная СС находилась в равновесии, необходимо и достаточно, чтобы выполнялись равенства
, 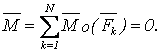 (3.1) (3.1)
Эти условия эквивалентны аналитическим условиям равновесия в виде
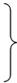 , , , , , ,
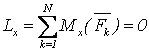 , , 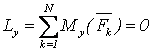 , , 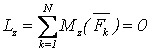 , (3.2) , (3.2)
т.е., для равновесия произвольной СС, приложенных к АТТ, необходимо и достаточно равенства нулю сумм проекций всех сил на оси декартовой системы координат и сумм моментов всех сил относительно этих осей.
Условия равновесия для пространственной системы параллельных сил (ось Oz параллельна ЛД сил) имеют вид
, 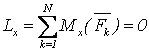 , , 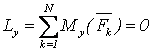 . (3.3) . (3.3)
Первая форма условий равновесия произвольной плоской СС: необходимо и достаточно, чтобы суммы проекций всех сил на две оси и сумма алгебраических моментов сил относительно любого центра были равны нулю
, , 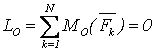 . (3.4) . (3.4)
Вторая форма:
, , ( не перпендикулярна ). (3.5)
Третья форма
, , (А,В,С - не на 1прямой ) (3.6)
Условия равновесия для плоской системы параллельных сил имеют вид
, ( не перпендикулярна силам) (3.7)
или , ( силам). (3.8)
Трение. Силы трения скольжения.
Законы трения скольжения (Кулона – Амонтона):
1) При стремлении сдвинуть одно тело относительно другого в плоскости их соприкосновения возникает сила трения , модуль которой 0≤F≤ Fmax. Эта сила приложена к телу и направлена в сторону, противоположную возможному направлению скорости точки приложения силы.
2) Максимальная сила трения равна произведению коэффициента трения f на силу нормального давления N
Fmax=f∙N. (3.9)
f зависит от материалов и состояния поверхностей соприкасающихся тел (шероховатость, температура, влажность и т. п.); определяется опытным путем. Значения f: дерево по дереву 0,4-0,7; металл по металлу 0,15-0,25.
Различают коэффициенты трения покоя и трения скольжения. Коэффициент трения покоя определяется по максимальной силе трения Fmax, соответствующей предельному состоянию равновесия. Обычно он больше коэффициента трения скольжения. С увеличением скорости скольжения последний сначала несколько уменьшается, а затем практически остается неизменным.
3) Fmax не зависит от площади соприкасающихся поверхностей.
Р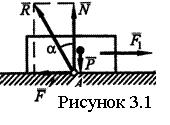 еакцию шероховатой поверхности представляют в виде нормальной реакции (равна по модулю силе нормального давления) и силы трения (см. рисунок 3.1). Полная реакция отклонена на угол α (tg α = F/N). еакцию шероховатой поверхности представляют в виде нормальной реакции (равна по модулю силе нормального давления) и силы трения (см. рисунок 3.1). Полная реакция отклонена на угол α (tg α = F/N).
Если тело лежит на горизонтальной шероховатой поверхности и на него не действуют никакие внешние силы, кроме силы тяжести, то F = 0, а полная реакция R = N и перпендикулярна опорной поверхности. Приложив к телу силу , мы стремимся вызвать его движение, но оно не происходит, так как возникает сила трения , причем F≤ Fmax. С увеличением возрастает и . При F1 = Fmax наступит предельное состояние равновесия, при котором полная реакция отклонится от вертикали на угол αmax, называемый углом трения. Обозначив его через φ, находим tg φ= Fmax/N=f . (3.10)
Полная реакция неидеальной связи при равновесии имеет направление в пределах угла трения. Равновесие тел с учетом сил трения скольжения рассматривают обычно для предельного состояния, когда сила трения достигает максимального значения.
Центр тяжести. Центр тяжести простейших тел.
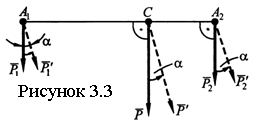 
Рассмотрим две параллельные силы и , приложенные к телу в точках А1и A2 (см. рисунок 3.3). Равнодействующая , ее ЛД параллельна слагаемым силам и проходит через некоторую точку С, лежащую на прямой A1A2,. Положение точки С найдем с помощью теоремы Вариньона 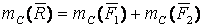 , откуда , откуда
. (3.12)
Повернув силы и на угол α вокруг точек А1, А2, придем к выводу, что иравнодействующая поворачивается в ту же сторону на угол α и приложена в той же точке С, называемой центром параллельных сил.Аналогично - для любого числа сил.
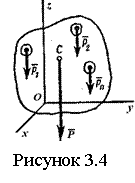
Равнодействующую сил тяжести , ,…, , приложенных к частицам тела, обозначим (см. рисунок 3.4). Модуль этой силы называется весом тела и он равен
. (3.13)
Точка С является центром параллельных сил тяжести и называется центром тяжести тела. Т.о., центр тяжести АТТ - неизменно связанная с телом точка, через которую проходит ЛД равнодействующей сил тяжести, приложенных к частицам данного тела, при любом положении тела в пространстве. Координаты его определяются как
, , (3.14)
где , , – координаты точек приложения сил тяжести .
|
|
|
 Скачать 1.03 Mb.
Скачать 1.03 Mb.

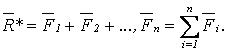 (1.1)
(1.1)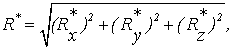 (1.3)
(1.3)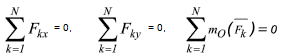


 . (2.9)
. (2.9)
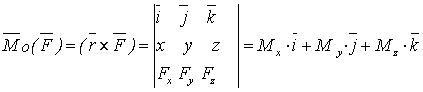 ,
,
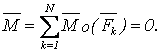 (3.1)
(3.1)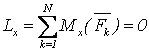 ,
, 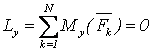 ,
, 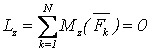 , (3.2)
, (3.2)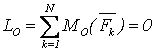 . (3.4)
. (3.4) еакцию шероховатой поверхности представляют в виде нормальной реакции (равна по модулю силе нормального давления) и силы трения (см. рисунок 3.1). Полная реакция отклонена на угол α (tg α = F/N).
еакцию шероховатой поверхности представляют в виде нормальной реакции (равна по модулю силе нормального давления) и силы трения (см. рисунок 3.1). Полная реакция отклонена на угол α (tg α = F/N).
