Билеты. БИЛЕТЫ. Основные понятия и аксиомы статики
 Скачать 1.03 Mb.
|
|
Основные понятия и законы динамики. В динамике рассматривают движение материальных тел под действием приложенных к ним сил с учетом инерции. Инерция - свойство тела сохранять состояние движения или покоя при отсутствии действующих на него сил. Мерой инерции тела в поступательном движении является его массаm. Основой динамики точки являются 4 аксиомы, изложенные ниже. 1. МТ, к которой не приложены силы, находится в состоянии покоя или равномерного прямолинейного движения, пока приложенные к ней силы не изменяют этого состояния. Движение МТ при отсутствии сил называют инерциальным. СО, в которой справедлива аксиома, называют инерциальной СО. 2. Ускорение МТ пропорционально приложенной силе и направлено так же, как сила. Основное уравнение . (6.1) 3. Две МТ действуют друг на друга с равными по модулю силами, лежащими на соединяющей их прямой и направленными противоположно. 4. Геометрическая сумма ускорений, которые сообщаются МТ отдельно каждой приложенной к ней силой, равна ускорению, которое МТ получит под действием на нее всех сил (6.2) Под действием на любое тело сил тяжести у тела возникает одно и то же ускорение , которое называют ускорением силы тяжести (ускорением свободного падения). Если к МТ приложена только сила тяжести , то по (6.1) . (6.3) Масса тела не зависит от его местонахождения и от сил, приложенных к телу, а вес тела меняется с изменением ускорения силы тяжести в зависимости от географической широты места и расстояния от центра Земли. Дифференциальные уравнения движения материальной точки и их интегрирования. Рассмотрим движение МТ под действием сил { } относительно инерциальной СО Оxyz, считая, что среди сил имеются реакции связей. Проецируя (6.2) на декартовы оси координат или естественные оси, получаем дифференциальные уравнения движения (ДУД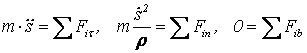)  (6.4)или  (6.5)ДУД применяют к решению двух основных задач динамики МТ: а) по движению точки найти приложенную к ней силу; б) по силам, приложенным к точке, найти ее движение. Принцип Даламбера. Силы инерции, действующие на точки МС, можно привести к главному вектору и главному моменту (точка O – неподвижный центр приведения). Тогда систему, находящуюся в движении, можно рассматривать как находящуюся в состоянии равновесия, включая в число и . Можно доказать, что при любом движении системы . Для АТТ, совершающего плоскопараллельное движение в плоскости материальной симметрии тела Oxy, силы инерции могут быть приведены к подвижному центру масс С. Тогда ось Cz - главная центральная ось инерции тела. Если - момент инерции относительно этой оси и ε – угловое ускорение, то . Основные теоремы динамики для материальной точки и механической системы. Теорема об измененииколичества движения системы Количеством движения системы (КДС) называют величину . (7.20) Можно показать, что , (7.21) т. е. КДС равно произведению массы всей системы на скорость ее центра масс. Если система движется так, что центр масс остается неподвижным, то КДС равно нулю (например, в случае тела, вращающегося вокруг неподвижной оси, проходящей через его центр масс). Если же движение тела является сложным, то величина КДС не зависит от его вращательного движения вокруг центра масс (для катящегося колеса независимо от вращения). Теорема об изменении КДС в дифференциальной форме: производная по времени от количества движения системы равна геометрической сумме всех действующих на систему внешних сил . (7.22) В интегральной форме: изменение КДС за некоторый промежуток времени равно сумме импульсов, действующих на систему внешних сил за тот же промежуток времени . (7.23) Следствие (закон сохранения КДС): внутренние силы не могут изменить КДС, и при решении задач внутренние силы можно не рассматривать. Теорема об изменении главного момента количеств движения Главным моментом количеств движения системы (ГМКДС) или кинетическим моментом относительно данного центра О называется величина , равная геометрической сумме моментов количеств движения всех точек системы относительно этого центра . (7.24) Аналогично имеем относительно координатных осей , , . (7.25) Теорема об изменении ГМКДС (теорема моментов): производная по времени от ГМКДС относительно некоторого неподвижного центра равна сумме моментов всех внешних сил системы относительно того же центра . (7.26) Проецируя на неподвижные оси 0хyz, получим теорему в проекциях. Теорема применяется для изучения вращательного движения тела, а также движения системы в общем случае, т.к. последнее слагается из поступательного и вращательного движения. Если за полюс выбрать центр масс, то поступательная часть движения тела может быть изучена с помощью теоремы о движении центра масс, а вращательная - с помощью теоремы моментов. При этом из рассмотрения исключаются наперед неизвестные внутренние силы. Для системы координат, движущейся поступательно вместе с телом, справедлива теорема моментов относительно его центра масс. Она имеет тот же вид, что и относительно неподвижного центра. Для моментов относительно осей такой системы также получаются схожие уравнения. Следствие из теоремы (закон сохранения ГМКДС): внутренние силы не изменяют ГМКДС. При этом если система неизменяема, то она вращается с постоянной угловой скоростью, а если изменяема, то под действием внутренних (или внешних) сил расстояния отдельных ее точек от оси могут изменяться, что вызовет изменение угловой скорости. Теорема об изменении кинетической энергии системы Кинетической энергией (КЭ) системы называют скалярную величину . (7.27) КЭ является характеристикой и поступательного, и вращательного движений системы. Отличие Т от и состоит в том, что КЭ является скалярной существенно положительной величиной, и наее изменение влияет действие и внешних, и внутренних сил. КЭ тела при поступательном, вращательном и плоскопараллельном движениях: , (7.28) , (7.29) . (7.30) Теорема об изменении КЭ сиcтемы в дифференциальной форме  (7.31)В интегральной форме: изменение КЭ при некотором перемещении равно сумме работ на этом перемещении всех внешних и внутренних сил . (7.32) Теорема о движении центра масс системы С учетом формулы (7.2) можно получить соотношение . (7.19) Это теорема о движении центра ЦМС: ЦМС движется как МТ, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему. Проецируя обе части равенства (7.19) на координатные оси, можно получить ДУД ЦМС в проекциях. Из (7.19) следует, что поступательно движущееся тело можно рассматривать как МТ с массой, равной массе тела. В остальных случаях тело можно рассматривать как МТ, когда допустимо не принимать во внимание вращательную часть движения. При определении закона движения ЦМС можно исключать из рассмотрения все неизвестные внутренние силы. Следствие из теоремы (закон сохранения движения центра масс): внутренние силы не изменяют движение ЦМС. Работа силы, мощность. Элементарная работа силы , приложенной в точке М (см. рисунок 6.1), определяется, как d 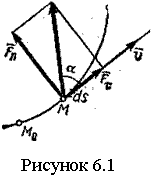 W = F∙ds (6.21)где F — проекция силы на касательную М к траектории точки М, направленную в сторону перемещения точки; ds — модуль элементарного перемещения точки М. Т.к. ds = |d | (здесь d - вектор элементарного перемещения точки), то равенство (6.21) можно представить в виде dW= . (6.22) Т.е., элементарная работа силы равна скалярному произведению силы на вектор элементарного перемещения точки ее приложения. Работа силы на конечном перемещении M0M1 определяется, как 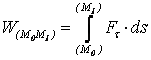 , (6.23) . ( 6.24)Мощность есть работа, совершаемая силой в единицу времени, , (6.25) т.е., мощность равна произведению касательной составляющей силы на скорость. Общие принципы расчета элементов конструкции Наиболее распространенным методом расчета на прочность является расчет по напряжениям: считается, что критерием надежности конструкции является напряжение (напряженное состояние) в точке. При этом на основании анализа конструкции выявляются наибольшие (расчетные) напряжения, которые сопоставляются с предельным значением для данного материала, полученным на основе испытаний; из сопоставления делается заключение о прочности. Если необходимо добиться наименьших изменений формы конструкции, производится расчет на жесткость, что не исключает проверки системы на прочность. Существуют другие методы, связанные с такими явлениями, как устойчивость, эффект повторных нагрузок, динамическое воздействие и др. Вопрос же о степени надежности конструкции в конкретных условиях изучается в курсах деталей машин и в спецкурсах. Растяжение и сжатие стержней. Реальный объект и расчетная схема Растяжение - вид нагружения стержня, при котором в его поперечных сечениях возникает только нормальная сила N. При растяжении направление N совпадает с направлением внешней нормали к рассматриваемому сечению. Сжатие формально отличается от растяжения только направлением N, хотя имеются и существенные отличия (сжатие длинных стержней сопровождается изгибом, характер разрушения при растяжении и сжатии различен). Обычно растяжение или сжатие возникает при нагружении стержня осевыми силами. Эпюру N строят с использованием метода сечений, при этом N равна сумме проекций на продольную ось всех сил, расположенных по одну сторону от рассматриваемого сечения N= ∑Fiz. (9.1) Растягивающую силу N считают положительной, сжимающую – отрицательной. Тогда проекция внешней силы в правой части (9.1) должна браться со знаком «+», если сила направлена от сечения, и со знаком «-», если направлена к сечению. Зависимость между нормальной силой и напряжениями в этом сечении имеет вид (9.2) где σ – нормальное напряжение в произвольной точке сечения, принадлежащей малой площадке dA; A – площадь поперечного сечения. И  з схемы деформирования стержня на рисунке 9.1 можно прийти к выводу, что напряжения во всех точках поперечного сечения одинаковы, так что откуда (9.3)Нормальное напряжение считается положительным при растяжении и отрицательным при сжатии. В рассматриваемом примере имеем однородное напряженное состояние – во всех точках стержня напряженное состояние одно и то же. Если стержень имеет переменное сечение, то при таком же нагружении напряженное состояние неоднородно. Метод сечений. Внутренние силовые факторы в поперечном сечении стержня П 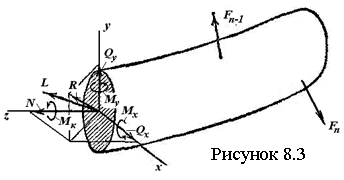 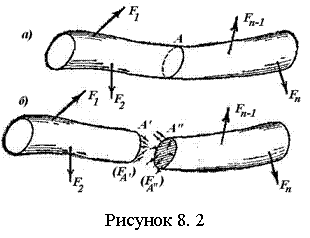 усть к стержню (см. рисунок 8.2,а) приложена нагрузка {F1, F2, …, Fn}. Внутренние силы, возникающие в стержне, выявляются, если рассечь его мысленно на две части, например, сечением А (это метод сечений). Т.к. связи между частями стержня устранены, необходимо действие правой части на левую и левой на правую заменить системой внутренних сил {FА} в сечении (см. рисунок 8.2,б). Система сил, возникающих в плоскости А', обратна по знаку системе сил в плоскости А". Внутренние силы распределяются некоторым сложным образом по сечению. При этом условия равновесия для правой и левой частей стержня должны удовлетворяться по отдельности. Главный вектор и главный момент внутренних сил в сечении А могут определяться из условий равновесия любой из частей тела.Из уравнений равновесия можно определить только статические эквиваленты внутренних сил (при условии, что внешние силы заданы). Приведем систему внутренних сил к центру тяжести сечения. В результате получим главный вектор и главный момент (см. рисунок 8.3). Выберем систему координат, направив ось z по нормали к сечению, а оси х и у расположим в его плоскости. Спроецировав и на оси, получаем 3 силы и 3 момента, которые называют внутренними силовыми факторами (ВСФ) в сечении стержня. Составляющую N называют нормальной (продольной) силой, Qx и Qy - поперечными силами, Мк - крутящим моментом, а Мх и Му - изгибающими моментами относительно осей х и у. При известных внешних силах все ВСФ определяются из шести уравнений равновесия. Аналогично классифицируются основные виды нагружения (растяжение, сжатие, кручение, изгиб и др.). Для определения вида нагружения, необходимо воспользоваться методом сечений и выявить, какие ВСФ возникают в его сечениях. Результаты определения ВСФ представляют в виде графиков (эпюр). |