Билеты. БИЛЕТЫ. Основные понятия и аксиомы статики
 Скачать 1.03 Mb.
|
|
Геометрические характеристики поперечных сечений. Статические моменты и центр тяжести плоской фигуры Рассмотрим некоторую плоскую фигуру в системе координат x, y (рисунок 11.1). Интегралы 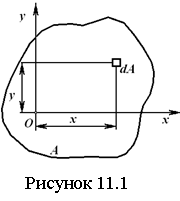 , (11.1)называются статическими моментами фигуры относительно оси x и оси y соответственно. Выясним, как изменяются статические моменты сечения при параллельном переносе координатных осей (см. рисунок 11.2). Очевидно, что x = x1 - a; y = y1 - b. Тогда 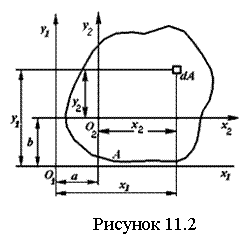 ,  .Величины а и b можно подобрать так, чтобы и были равны нулю. Ось, относительно которой статический момент равен нулю, называется центральной. Точка пересечения центральных осей называется центром тяжести фигуры; в системе координат (x1, y1) координаты центра тяжести равны , . (11.2) Отметим, что статический момент составного сечения равен сумме статических моментов составляющих областей. 11.2 Моменты инерции сечения Возвращаясь к рисунку 11.1, рассмотрим три интеграла , (11.3) , (11.4) . (11.5) Первые два интеграла называют осевыми моментами инерции относительно осей x и y соответственно, третий центробежным моментом инерции сечения относительно осей x, y. Осевые моменты всегда положительны, центробежный может быть как положительным, так и отрицательным. При параллельном переносе осей координат (см. рисунок 11.2) имеем , (11.6) , (11.7) . (11.8) Если x1 и y1 - центральные, то и тогда , (11.9) , (11.11) . (11.11) Т.о., при параллельном переносе осей в случае, когда одна из осей – центральная, осевые моменты инерции изменяются на величину, равную произведению площади на квадрат расстояния между осями. В семействе параллельных осей момент инерции относительно центральной оси минимален. 11.3 Главные оси и главные моменты инерции Рассмотрим, как изменяются моменты инерции плоского сечения при повороте осей координат из положения x и y к положению u и v. Из рисунка 11.3 легко установить, что u = y∙sin+ x∙cos; v = y∙cos x∙sin. (11.13) И 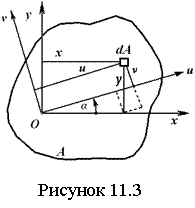 з выражений , , с учетом (11.13) после несложных преобразований получим, (11.14) , (11.15)  . (11.16)Складывая первые два уравнения, получаем  (11.17) т.е., сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей при повороте осей постоянна и равна полярному моменту инерции фигуры. Т.к. с изменением угла значения и изменяются, а их сумма остается постоянной, то существует такое значение =0, при которомодин из моментов или достигает своего максимального значения, другой – минимального. Значение 0 найдем, исследуя на экстремум или . Найдем . (11.18) Оказывается, что при =0 одновременно центробежный момент инерции обращается в нуль. Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения, называются главными осями инерции. Осевые моменты инерции относительно главных осей называются главными моментами инерции. Они определяются с использованием (11.14), (11.15) и (11.18) как  . (11.19)Кинематика точки. Способы задания движения. 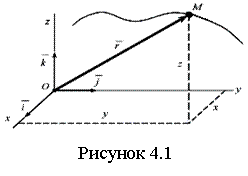 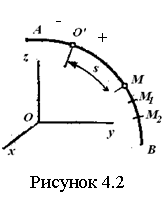 Под движением понимают изменение с течением времени положения данного тела в пространстве по отношению к другим телам, образующим вместе с системой координат систему отсчета (СО). Движение тел совершается в пространстве с течением времени. Пространство - трехмерное евклидово, время протекает одинаково во всех СО. В задачах кинематики время t принимают за аргумент, все другие переменные (расстояния, скорости и т. д.) рассматривают как функции от t. Отсчет времени ведется от некоторого начального момента. Для решения задач надо, чтобы движение тела (точки) было кинематически задано, что означает задание положения тела (точки) относительно данной СО в любой момент времени. Изучение движения начинается с установления способов задания движения. Основная задача кинематики - зная закон движения точки (тела), установить методы определения всех кинематических величин. Непрерывную линию, описываемую точкой относительно данной СО, называют ее траекторией (прямолинейное и криволинейное движения). Движение точки может быть задано 3 способами. 1. Векторный способ. Положение точки определяется ее радиус-вектором (см. рисунок 4.1) . (4.1) 2. Координатный способ. Положение точки определяют ее координатами . (4.2) 3. Естественный способ. Задают (рисунок 4.2) траекторию точки, начало отсчета на траектории с указанием направлений отсчета и закон движения в виде . (4.3) Скорость и ускорение точки. Доказывается (см. рисунок 4.3), что скорость есть первая производная от вектора по аргументу t . (4.4) У 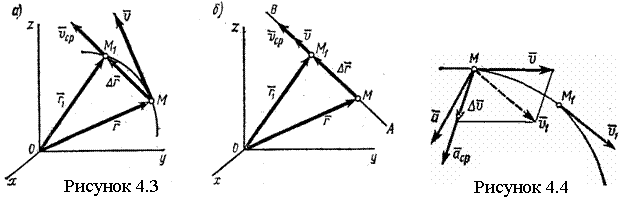 скорением точки в данный момент времени t (см. рисунок 4.4) называют векторную величину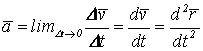 . (4.5)Т.о., вектор ускорения точки равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени. Чтобы определить скорость точки при координатном способе задания движения, используем теорему: проекция производной от вектора на неподвижную ось равна производной от проекции вектора на ту же ось. Тогда для проекций скорости имеем (4.6) или . (4.7) Для проекций ускорения имеем , , (4.8) или . (4.9) При естественном способе задания движения скорость и ускорение точки определяют по их проекциям на оси естественного трехгранника Мnb, имеющие начало в точке М и движущиеся вместе с нею. Направления осей: М - по касательной к траектории в сторону положительного отсчета s; главная нормаль Мn - по нормали к траектории, лежащей в соприкасающейся плоскости, и направленной в сторону вогнутости траектории; бинормаль Mb - перпендикулярно к первым двум так, чтобы она образовывала с ними правую систему осей. Определим скорость точки 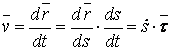 . (4.10)Проекция скорости точки на касательную к ее траектории . (4.11) Очевидно, что и модуль скорости . Для ускорения точки имеем 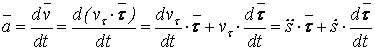 . (4.12)Т.к. 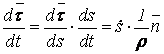 (ρ – радиус кривизны траектории точки), то, (4.13) т.е., ускорение равно сумме касательной и нормальной составляющих . (4.14) Вектор лежит в соприкасающейся плоскости, т. е. в плоскости Mn. Проецируя обе части равенства (4.13) на оси М, Мn и Mb, получим 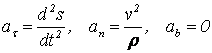 . (4.15)Простейшие движения твердого тела. Поступательное движение и вращение вокруг неподвижной оси. Поступательным называется такое движение АТТ, при котором любая прямая, проведенная в теле, перемещается, оставаясь параллельной себе, при этом траектории его точек могут быть любыми кривыми. Справедлива теорема: при поступательном движении все точки тела описывают одинаковые траектории и имеют в любой момент времени одинаковые по модулю и направлению скорости и ускорения. Здесь кинематика АТТ сводится к кинематике точки. П 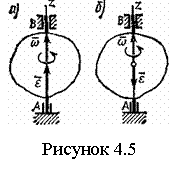 ри вращении АТТ вокруг неподвижной оси, его точки, лежащие на оси, остаются неподвижными (АВ на рисунке 4.5). Через ось проведем две плоскости - неподвижную и подвижную, связанную с телом. Двугранный угол между ними (угол поворота тела) считают положительным, когда он отсчитывается от неподвижной плоскости к подвижной против часовой стрелки, если смотреть со стороны положительного направления оси. Закон движения = (t). (4.16) Угловая скорость характеризует изменение = d/dt или . (4.17) Угловую скорость тела можно изобразить в виде вектора. Угловое ускорение характеризует изменение ω с течением времени = d/dt = d2/dt2 или . (4.18) Если во все время движения =const, то вращение называют равномерным. Из (4.17), интегрируя, найдем его закон . (4.19) При равномерном вращении, если , то . (4.20) Е 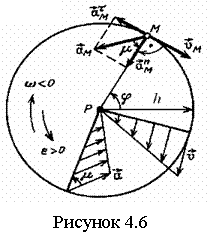 сли =const, то вращение называется равнопеременным, его закон (4.21)Если и одного знака, вращение - равноускоренное, если разного - равнозамедленное. Определим скорости и ускорения точек вращающегося тела (см. рисунок 4.6). Имеем 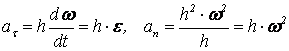 , (4.22) . (4.23)Ускорение направлено по касательной к траектории (в сторону движения при ускоренном вращении, в обратную при замедленном), ускорение - по радиусу МP к оси. Полное ускорение точки и угол (рисунок 4.6) определяются как , (4.24) . (4.25) Сложное движение точки 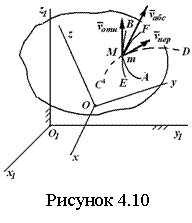 В ряде случаев удобно рассматривать движение точки по отношению к двум СО, из которых одна считается основной (условно неподвижной), а другая - движущейся по отношению к первой. Рассмотрим точку М, движущуюся по отношению к подвижной СО Oxyz, которая, в свою очередь, движется относительно неподвижной СО О1х1у1z1 (см. рисунок 4.10). Введем определения: а) движение, совершаемое точкой по отношению к подвижной СО (к осям Oxyz), называется относительным; б) движение, совершаемое подвижной СО Oxyz по отношению к неподвижной системе О1х1у1z1, для точки М является переносным движением. Скорость неизменно связанной с подвижными осями Охуz точки m, с которой в данный момент времени совпадает движущаяся точка М, называется переносной скоростью точки М ( ), а ускорение этой точки m - переносным ускорением точки М. Тогда , ; (4.31) в) движение, совершаемое точкой по отношению к неподвижной системе отсчета О1х1у1z1, называют абсолютным или сложным. Доказывается, что в случае сложного движения справедливо соотношение . (4.32) Направлены по касательным к соответствующим траекториям. Если угол между и равен , то  . (4.33)Для ускорений имеем . (4.34) Это - теорема Кориолиса о сложении ускорений: при сложном движении ускорение точки равно геометрической сумме трех ускорений, относительного, переносного и поворотного (кориолисова). Доказывается, что . (4.35) Если переносное движение является поступательным движением, то . (4.36) |