Билеты. БИЛЕТЫ. Основные понятия и аксиомы статики
 Скачать 1.03 Mb. Скачать 1.03 Mb.
|
|
Практические расчеты сварных, заклепочных и других видов соединений при сдвигах. Обычно сдвиг сопровождается смятием, изгибом, концентрацией напряжений, контактными напряжениями. Касательные напряжения при сдвиге оказываются распределёнными неравномерно. Далее речь будет идти о так называемых практических расчётах на сдвиг. Условие прочности при расчёте на сдвиг имеет вид  Здесь Q — сдвигающая сила; А — площадь сдвига; iadm — допускаемое касательное напряжение в расчётах на сдвиг (устанавливается нормами, техническими условиями и т.п.). Условие прочности на смятие, часто сопровождающее сдвиг, имеет вид 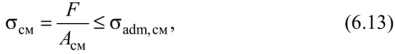 где асм — сминающее напряжение; F — сминающая сила; Аш — площадь смятия; ааат,см — допускаемое нормальное напряжение в расчётах на смятие. Заклёпочные соединения являются неразъёмными, а болтовые — разъёмными соединениями, но их расчёты на прочность во многом одинаковы. Введём допущения. 1. Усилия между заклёпками (болтами) распределены равномерно (на каждую заклёпку или болт приходится одинаковая сила). 2. Силы трения, возникающие между соединяемыми элементами, не учитываются. Рассмотрим расчёт заклёпочных соединений на срез. Будем считать касательные напряжения по поперечному сечению заклёпки распределёнными равномерно. Используя формулу (6.12), запишем условие прочности заклепок на срез (рис. 6.2):  где F — сдвигающая сила; d — диаметр заклёпки; пср — число заклёпок в заклёпочном соединении из условия прочности на срез; т — число срезов у одной заклёпки. Оно на единицу меньше числа деталей, соединяемых заклёпкой. На рис. 6.2 изображено односрезное соединение (т = 1) листов внахлестку. Изобразим заклёпочное соединение с двумя накладками (рис. 6.3): здесь т - 2, это двусрезное соединение. 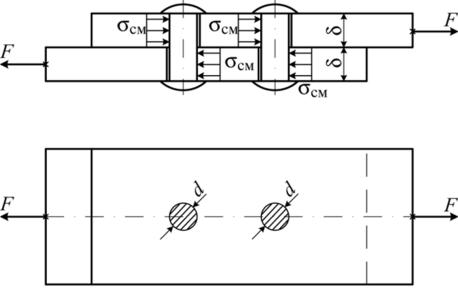 Рис. 6.2 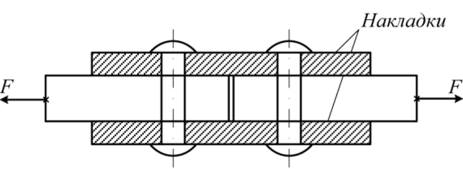 Рис. 6.3  Рассмотрим расчёт заклёпочного соединения на смятие. Для установки заклёпок в предназначенные для них отверстия в листах диаметр отверстий должен быть больше диаметра заклёпок. Когда сформировалась вторая головка заклёпки, диаметр стержня заклёпки несколько увеличится, но зазор между заклёпкой и листами может сохраниться. Под действием сдвигающих сил F (см. рис. 6.2) листы смещаются и зазор между заклёпкой и отверстием с одной стороны закрывается, цилиндрическая поверхность заклёпки подвергается смятию на площадке контакта с цилиндрической поверхностью отверстия. Примерный вид эпюры сминающих напряжений по периметру заклёпки показан на рис. 6.4, а. По толщине листа напряжения асм считаем распределёнными равномерно. 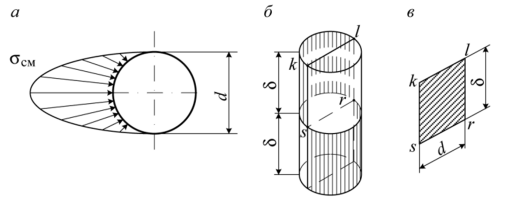 Рис. 6.4 На рис. 6.4, б вертикальными штрихами показаны части поверхности заклёпки, подвергающиеся смятию (рис. 6.4 соответствует заклёпочному соединению, изображённому на рис. 6.2). В практических расчётах условно считаем напряжения стсм распределёнными равномерно по диаметральной плоскости продольного сечения заклёпки klrs (рис. 6.4, в). Тогда на основании формулы (6.13) условие прочности односрезного заклёпочного соединения на смятие примет вид  где 8 — толщина листов; пш — число заклёпок из условия прочности на смятие, остальные обозначения пояснены раньше. Если соединение многосрезное, то вместо 5 в формулу (6.16) подставляем (minZS) — минимальную сумму толщин листов, примыкающих к заклёпке с одной стороны стыка: 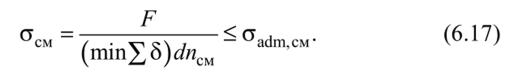 Из формулы (6.17) определим число заклёпок из условия прочности на смятие:  Вычисление величины (minZ5) поясним примером (рис. 6.5). 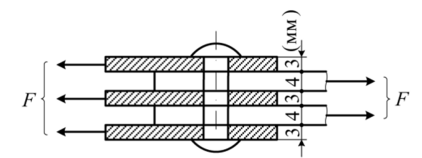 Рис. 6.5 Слева в соединении — три листа толщиной по 3 мм (в сумме 9 мм), а справа — два листа толщиной по 4 мм (в сумме 8 мм), то есть (minZ5) = 8 мм. Из двух чисел пср (формула (6.15)) и псм (формула (6.18)) принимаем в качестве числа заклёпок большее число. Если соединение с накладками (см. рис. 6.3), то найденное большее число необходимо удвоить, ибо найденное п — это число заклёпок с одной стороны стыка (сначала заклёпки, стоящие слева от стыка, передают силу F с левого листа на накладки, а потом заклёпки, стоящие справа от стыка, передают силу F с накладок на правый лист). Стержень заклёпки подвергается изгибу. На основании рис. 6.2, заменив асм их равнодействующими, получим рис. 6.6, изобразив лишь одну заклёпку. Силы F с плечом 5 приводятся к паре сил с моментом F5, изгибающей стержень заклёпки. Реактивные силы R, возникающие между головками заклёпки и листами, приводятся к паре сил с моментом R-2е, уравновешивающей заклёпку. Силы R удлиняют стержень заклёпки, поэтому уменьшаются силы трения между соединяемыми листами, но поскольку силы трения изначально в расчёт не принимались, заклёпочное соединение приблизится к расчётной схеме. В ряде случаев необходимо обеспечить не только прочность, но и плотность заклёпочного соединения, то есть непроницаемость его для жидкостей и газов, например, в резервуарах, котлах и т.п. Расчёт на плотность аналогичен расчёту заклёпок на срез, но при пониженных допускаемых напряжениях iadm на срез. Для односрезного соединения Tadm принимают 50-70 МПа, а для двусрезного соединения — 90—120 МПа. 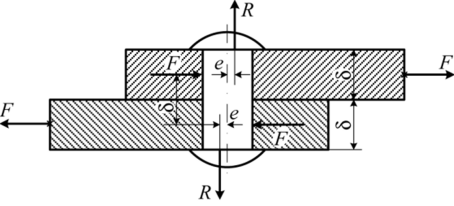 Рис. 6.6 Заклёпки ослабляют листы отверстиями для них (рис. 6.7). Проверяем прочность листов на разрыв: 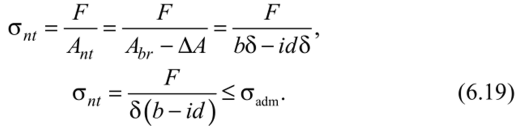 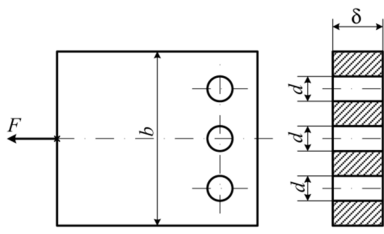 Рис. 6.7 В формуле (6.19) обозначены: b — ширина листов; i — число заклёпок в одном ряду (на рис. 6.7 i - 3). Расчёт болтовых соединений и расчёт заклёпочных соединений аналогичны. Цель расчёта сварных соединений — обеспечить равнопрочность основного и наплавленного металлов. Допускаемое напряжение сварного шва зависит от типа сварки (газо- или электросварка), от вида шва и от материала электрода. Допускаемое напряжение для сварного шва обычно меньше допускаемого напряжения материала электрода вследствие технологических дефектов Кручение стержней круглого поперечного сечения. Под кручением понимается такой вид нагружения стержня, при котором в его поперечных сечениях возникает только крутящий момент Мкр. Кручение обычно возникает при нагружении стержня парами сил (скручивающими моментами), плоскости действия которых перпендикулярны продольной оси стержня. Эпюру крутящего момента строят с использованием метода сечений, при этом Мкр равен сумме моментов относительно продольной оси стержня всех пар сил, расположенных по одну сторону от рассматриваемого сечения Мкр = ∑Mi. (10.2) Правило знаков: если наблюдатель со стороны внешней нормали к сечению видит момент Мкр направленным против часовой стрелки, то он считается положительным, иначе - отрицательным. Внешние моменты в (10.2) должны браться с противоположным правилом. При расчете стержня (вала) обычно требуется определить напряжения и угловые перемещения в зависимости от величин внешних моментов. Методами СМ можно получить решение только для стрежня кругового или кольцевого поперечного сечения (будем рассматривать только этот случай) и для тонкостенных стержней. В случае кручения стержня с круговым поперечным сечением каждое сечение стержня поворачивается в своей плоскости на некоторый угол как жесткое целое (гипотеза плоских сечений). Р  ассмотрим стержень с круговым поперечным сечением, показанный на рисунке 10.2,а. В его поперечных сечениях возникает постоянный крутящий момент Мкр=M. Двумя поперечными сечениями, выделим из стержня элемент длиной dz, а из него свою очередь двумя цилиндрическими поверхностями с радиусами и (+d) – элементарное кольцо, показанное на рисунке 10.2,в. В результате кручения правое торцевое сечение кольца повернется на угол d. Тогда ассмотрим стержень с круговым поперечным сечением, показанный на рисунке 10.2,а. В его поперечных сечениях возникает постоянный крутящий момент Мкр=M. Двумя поперечными сечениями, выделим из стержня элемент длиной dz, а из него свою очередь двумя цилиндрическими поверхностями с радиусами и (+d) – элементарное кольцо, показанное на рисунке 10.2,в. В результате кручения правое торцевое сечение кольца повернется на угол d. Тогда. (10.3) Угол представляет собой угол сдвига цилиндрической поверхности под действием касательных напряжений . Величину (10.4) называют относительным углом закручивания. Это угол взаимного поворота двух сечений, отнесенный к расстоянию между ними. Из рассмотрения (10.3) и (10.4) получим = ∙θ. (10.5) или . (10.12) Величина (10.13) называется полярным моментом сопротивления поперечного сечения стержня. Формулы (10.10), (10.12) справедливы для кругового и кольцевого сечений. Полярный момент инерции для круглого сечения найдем из (10.7), учитывая, что элементарная площадь пояска dA=2π∙ρ∙dρ (рисунок 10.3). Имеем 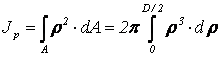 или .(10.14) или .(10.14)Полярный момент сопротивления для круглого сечения . (10.15) Для кольцевого сечения (с наружным D и внутренним d диаметрами) имеем 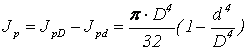 .(10.16) .(10.16)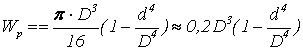 . (10.17) . (10.17)Условие прочности и условие жесткости при кручении имеют вид , (10.18) 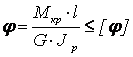 или или 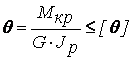 (10.110) (10.110)где [τ], [φ], [θ] – допускаемое касательное напряжение, допускаемый полный и допускаемый относительный углы закручивания соответственно. Внутренние силовые факторы при изгибе. Рассмотрим брус, изображенный на рис. 16.3 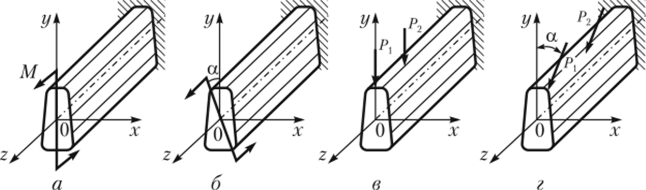 Рис. 16.3. Оси и плоскости бруса при изгибе: z — ось бруса; х и у — главные центральные оси поперечного сечения; плоскости xOz и yOz — главные продольные плоскости бруса Различают несколько видов изгиба. • Чистый изгиб возникает при нагружении бруса парами сил, т.е. моментами, плоскость действия которых совпадает с продольной плоскостью бруса. Чистый изгиб может быть прямой или косой: — прямой — если плоскость действия момента совпадает с одной из главных плоскостей бруса (см. рис. 16.3, а) — косой — если плоскость действия момента расположена под углом к главным плоскостям бруса (см. рис. 16.3, б). При чистом изгибе в поперечных сечениях действует только один внутренний силовой фактор — изгибающий момент.  • Поперечный изгиб возникает при нагружении бруса силами, перпендикулярными его оси. Поперечный изгиб также может быть прямой (см. рис. 16.3, в) и косой (см. рис. 16.3, г). При поперечном изгибе в сечениях бруса действуют два силовых фактора — поперечная сила и изгибающий момент. Брус, работающий на изгиб, обычно называют балкой. Не следует думать, что балка обязательно должна иметь большие размеры. Соединительный проводник микроэлектронного прибора длиной 3 мм и диаметром 30—40 мкм, нагруженный поперечной инерционной нагрузкой, также расситывается по схеме балки. Для определения силовых факторов в поперечных сечениях балок используется метод сечений Дифференциальные зависимости Журавского Доказывается, что между интенсивностью распределенной нагрузки, поперечной силой и изгибающим моментом имеют место зависимости , , . (11.22) Из (11.22), в частности, следует, что при q = const функция Q линейная, а функция M квадратичная. Если на какихто участках бруса распределенная нагрузка отсутствует (q = 0), то Q = const, а M - линейная функция от z. В сечениях, где Q принимает нулевое значение и меняет знак, функция Mx достигает экстремальных значений. Напряжение в поперечных сечениях стержня при чистом и при поперечном изгибе. Напряжения при чистом изгибе П 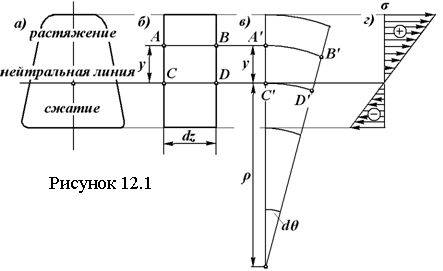 ри чистом изгибе имеем Q=0, M=const. Под действием M стержень изгибается. Принимая гипотезу плоских сечений, деформации можно рассматривать, как результат поворота одного поперечного сечения относительно другого (см. рисунок 12.1). Рассмотрим два сечения, расположенных на расстоянии dz друг от друга. В результате поворота правого сечения относительно левого на угол dθ верхние слои удлинятся, нижние укоротятся. Существует слой, в котором удлинения отсутствуют – это нейтральный слой CD. Между радиусом кривизны нейтрального слоя ρ, углом dθ и длиной dz существует зависимость dz= ρ∙dθ. Деформация произвольно взятого отрезка AB длинойdz равна ри чистом изгибе имеем Q=0, M=const. Под действием M стержень изгибается. Принимая гипотезу плоских сечений, деформации можно рассматривать, как результат поворота одного поперечного сечения относительно другого (см. рисунок 12.1). Рассмотрим два сечения, расположенных на расстоянии dz друг от друга. В результате поворота правого сечения относительно левого на угол dθ верхние слои удлинятся, нижние укоротятся. Существует слой, в котором удлинения отсутствуют – это нейтральный слой CD. Между радиусом кривизны нейтрального слоя ρ, углом dθ и длиной dz существует зависимость dz= ρ∙dθ. Деформация произвольно взятого отрезка AB длинойdz равна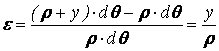 . (12.1) . (12.1)Согласно закону Гука . (12.2) Т.о., при чистом изгибе напряжения распределяются в поперечном сечении по линейному закону. Нейтральная линия (НЛ) – это геометрическое место точек, в которых σ=0; очевидно, она перпендикулярна плоскости кривизны изогнутого стержня. Т.к. 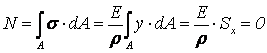 при чистом изгибе, то , т.е. НЛ проходит через центр тяжести поперечного сечения. Мы рассматриваем частный случай изгиба, при котором изогнутая ось стержня лежит в плоскости действия моментаM . Тогда при чистом изгибе, то , т.е. НЛ проходит через центр тяжести поперечного сечения. Мы рассматриваем частный случай изгиба, при котором изогнутая ось стержня лежит в плоскости действия моментаM . Тогда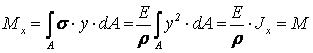 , (12.3) , (12.3)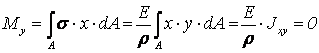 . (12.4) . (12.4)Из (12.4) следует, что , т.е., изменение кривизны стержня в плоскости момента M имеет место тогда, когда плоскость M проходит через одну из главных осей инерции сечения. Такой изгиб называют прямым в отличие от косого, при котором плоскость M и плоскость кривизны стержня не совпадают. Из (12.3) получаем выражение для кривизны стержня . (12.5) Здесь - момент инерции сечения относительно главной центральной оси, перпендикулярной плоскости изгибающего момента. Величина называется жесткостью стержня при изгибе. Подставляя (12.5) в (12.2), получаем выражение для напряжения σ . (12.6) Напряжения максимальны в точках, наиболее удаленных от НЛ, (12.7) где - момент сопротивления сечения изгибу. Условие прочности при чистом изгибе имеет вид (12.8) где - допускаемое напряжение. Отметим, что в случае материала стержня, неодинаково сопротивляющегося растяжению и сжатию, бывает необходимым выполнять расчет на прочность как по максимальным растягивающим, так и по максимальным сжимающим напряжениям. Наиболее экономичными являются такие формы поперечных сечений, для которых при одинаковой площади получаются наибольшие значения - это, например, стандартные прокатные профили типа двутавров, швеллеров. При поперечном изгибе Q≠0, M=vary, в поперечных сечениях стержней возникают не только нормальные напряжения σ, но и касательные τ. Возникновение τ сопровождается появлением угловых деформаций γ, и т.к. τ распределены по сечению неравномерно, поперечные сечения стержня не остаются плоскими. Однако на значениях σ это не очень сказывается, и формулы (12.5) и (12.6) можно считать справедливыми с достаточной точностью. Считая, что по ширине b напряжения τ распределены равномерно, удобно их определить через парные им напряжения в продольном сечении, расположенном на расстоянии y от НЛ (см. рисунок 12.2). Записывая уравнения равновесия для отсеченной продольным сечением части элемента длиной dz, получаем формулу Журавского для касательных напряжений (12.9) где - статический момент относительно оси x части площади, расположенной выше продольного сечения.
Во многих случаях τ не сказываются на прочности стержней (исключая тонкостенные и короткие стержни). Тогда для стержней постоянного поперечного сечения, изготовленных из материала, одинаково работающего на растяжение и сжатие, условие прочности при поперечном изгибе имеет вид  (12.10) (12.10)Основные теории напряженного и деформированного состоянии. Напряжённое и деформированное состояние частицы тела Теория НДС ставит своей задачей определение внутренних напряжений, деформаций и перемещений в различных точках деформируемого твёрдого тела произвольной формы и размеров. В нагруженном какой-то нагрузкой теле в каждой точке сеченияв общем случае возникают нормальное напряжение , направленное перпендикулярно к сечению, и касательное , лежащее в плоскости сечения. Как известно, через точку можно провести бесконечное количество плоскостей и в этой точке будут напряжения и , перпендикулярные и лежащие в этих плоскостях. Таким образом, напряженное состояние в точке можно представить совокупностью всех и , возникающих в ней. Для характеристики напряженного состояния в точке достаточно знать значения нормальных и касательных напряжений на трех взаимно перпендикулярных площадках (будет доказано позднее). Их удобнее представить в виде параллелепипеда с бесконечно малыми гранями. Поскольку расстояние между гранями бесконечно мало, то можно считать, что на противоположных гранях параллелепипеда возникают одинаковые по величине напряжения, но направленные противоположно. Напряженным состоянием тела в точке называют совокупность нормальных и касательных напряжений, действующих по трем взаимно перпендикулярным площадкам (сечениям), содержащим данную точку. Отнесём тело к координатным осям x, y, z и выделим мысленно из него материальную частицу в виде параллелепипеда или кубика размерами dx, dy, dz (рис. 3.1). 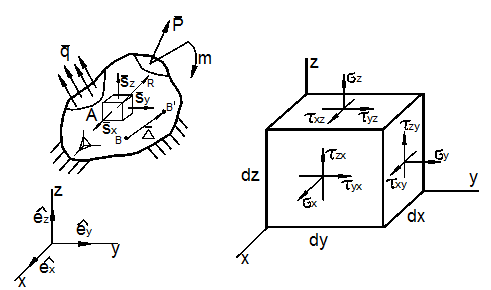 а) б) Рис. 3.1 Действия отброшенной части тела заменим векторами – напряжениями и разложим их на составляющие по координатным осям. 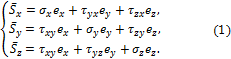 где ex, ey, ez - единичные векторы, направленные вдоль координатных осей x, y, z; - нормальные напряжения, Совокупность указанных напряжений полностью характеризует напряжённое состояние частицы тела. Эту совокупность записывают в виде квадратной матрицы и называют тензором напряжений Коши. Система напряжений, приложенных к частице тела, должна удовлетворять условиям равновесия. Первые три условия в проекциях на оси x, y, z дают тождества, т.к. на противоположных гранях мы считаем напряжения равными по величине. Остаётся проверить, обращаются ли в нуль суммы моментов всех сил относительно координатных осей. Составим условие равновесия моментов относительно оси х: откуда следует . Аналогично можно составить два уравнения равновесия моментов относительно осейy и z. В результате получим соотношения: которые называют законом парности касательных напряжений: на двух взаимно перепендикулярных площадках составляющие касательных напряжений, ортогональные их общему ребру, равны по величине и направлены оба либо к ребру, либо от него. На основании этого закона тензор-матрица напряжений является симметричной относительно главной диагонали, состоящей из нормальных напряжений. Напряжение называют средним напряжением. Тензор напряжений, для которого , называется тензором–девиатором напряжений. Напряженное состояние в точке можно представить как сумму состояний: напряженное состояние, в котором все три главные напряжения равны (всестороннее растяжение или сжатие) и напряженное состояние, на гранях которого нормальные напряжения представляют собой разность и . В общем случае тензор напряжений можно разложить на сумму двух тензоров: Первый из них носит название шарового тензора напряжений, а второй: тензора–девиатора или просто девиатора напряжений. Иногда компоненты девиатора напряжений обозначают: 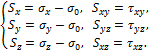 Шаровой тензор характеризует напряженное состояние всестороннего растяжения – сжатия частицы тела, а девиатор – напряженное состояние её формоизменения. На каждую частицу тела кроме напряжений действуют объёмные силы: где Rx, Ry, Rz – проекции этих сил на координатные оси. Каждая вектор-сила действует на единицу объёма. На поверхности тела F на каждую единицу её площади могут действовать распределённые силы: где qx, qy, qz– проекции этих сил. Если последние действуют на малых площадках контакта поверхности тела, то их, согласно принципу смягчения граничных условий Сен-Венана, заменяют главными вектором и моментом всех сил, действующих на этих малых площадках: где - радиус – вектор, проведённый из заданной точки (центра приведения сил) на до текущей силы . В результате действия на тело внешних сил температуры Т каждая точка В совершает перемещение в новое положение В’. Это перемещение характеризуется направленным отрезком , т.е. вектором перемещения: где u, v, w – проекции этого перемещения на координатные оси. Перемещения характеризуют деформацию тела в целом. Например, прогибы точек оси балки V и поворот поперечных сечений, проходящих через эти же точки, характеризуют деформацию балки в целом при её изгибе. Деформация тела складывается из деформации её материальных (физических) частиц, каждая из которых испытывает удлинения между её гранями в каждой из координатных плоскостей (рис. 3.2). Величины называют относительными удлинениями или деформациями частиц тела. Половины сдвигов обозначают: Совокупность шести компонентов деформации полностью характеризует деформированное состояние частицы тела. Эту совокупность запишем в виде квадратной матрицы: и назовем тензором деформаций Коши. 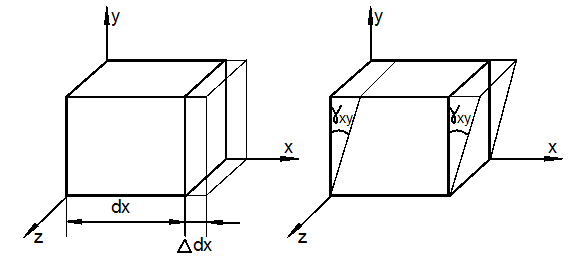 а) б) Рис. 3.2 Величину называют средней деформацией. Если для рассматриваемого тензора деформация , то он называется тензором-девиаторомили просто девиатором деформации. В общем случае тензор (7) можно разложить на сумму двух тензоров: Первый из них: носит название шарового тензора деформации и описывает объёмную деформацию всестороннего растяжения – сжатия. Второй тензор: представляет собой тензор-девиатор и характеризует деформацию изменения формы частиц тела. Главные площадки и главные напряжения. Виды напряженных состояний. Обобщенный закон Гука. Главными площадками называются такие взаимно перпендикулярные площадки, по которым действуют наибольшие и наименьшие нормальные напряжения, а касательные напряжения равны нулю. Напряжения, действующие по этим площадкам называются главными. Для нахождения угла наклона главных площадок нужно найти максимум и минимум нормальных напряжений. Для этого возьмем первую производную от выражения (10.1) и приравняем ее к нулю: 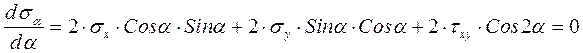 ,(11.1) ,(11.1)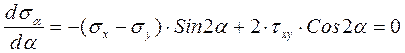 . (11.2) . (11.2)После деления каждого члена уравнения на получим: 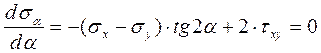 (11.3) (11.3)откуда 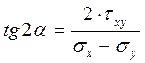 . (11.4) . (11.4)Учитывая, что , получим: 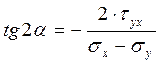 . (11.5) . (11.5)Полученные формулы(11.5), (11.4) дают возможность определить угол наклона главных площадок – α. Если α получится положительным, его следует отложить против часовой стрелки; и наоборот, если αотрицательный - по часовой стрелке. Так как угол 2 отличается от другого значения на 180°, то α будет отличаться на 90°. Отсюда следует, что главные площадки взаимно перпендикулярны. Подставив выражение (11.4) в (10.1), будем иметь формулу для определения величины главных напряжений: 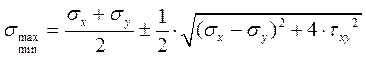 . (11.6) . (11.6)Как исходные нормальные напряжения σx, σy, так и главные считаются положительными, если они растягивающие и, наоборот, отрицательными, если они являются сжимающими. За положительное касательное напряжение τxy принимается такое, которое может осуществить вращение по часовой стрелке, и, наоборот, против часовой стрелки - считается отрицательным. Докажем, что в главных площадках касательные напряжения равны нулю. Для этого умножим все члены уравнения (11.2) на : 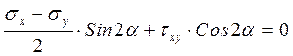 Полученное выражение для касательных напряжений равно нулю, что и требовалось доказать (см. 10.3). Различают три вида напряженных состояний 1. Объемное - когда все три главных напряжения отличны от нуля (рис.14в). 2. Плоское - когда одно из главных напряжений равно нулю (рис. 14б). 3. Линейное - когда два главных напряжения равны нулю (рис. 14а). Главные напряжения обозначают через σ1, σ2, σ3. Рассматривая их в порядке убывания, будем иметь: 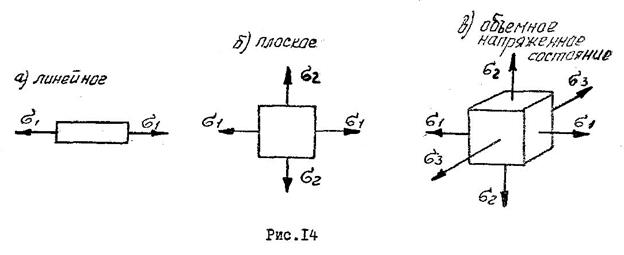 Деформации в направлении глазных напряжений - главные деформации в данной точке - определяются на основе обобщенного закона Гука: 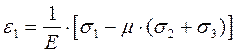 , (11.7) , (11.7)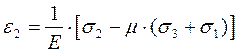 , (11.8) , (11.8)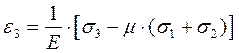 , (11.9) , (11.9)где μ - коэффициент Пуассона. В частных случаях приведенные формулы упрощаются. Так, для линейного напряженного состояния с σ1>0; σ2= σ3=0: ; 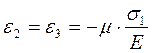 В случае, когда напряженное состояние во всех точках тела одинаково, такое напряженное состояние называется однородным. Обобщенный закон Гука относительно главных напряжений, для плоского напряженного состояния имеет вид: 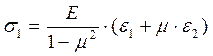 ; ; 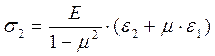 Относительная объемная деформация вычисляется по одной из формул: 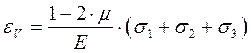 . (11.10) . (11.10)Напряжения на наклонных площадках вычисляются по формулам: при плоском напряженном состоянии: 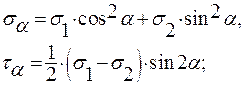 (11.11) (11.11)при линейном напряженном состоянии: 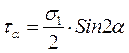 , (11.12) , (11.12)где ; - соответственно нормальное и касательное напряжение в наклонной площадке, проведенной под углом α. Теория прочности. Перечислим наиболее известные в сопротивлении материалов теории прочности. Первая теория прочности — Теория наибольших нормальных напряжений. Вторая теория прочности — Теория наибольших деформаций. Третья теория прочности — Теория наибольших касательных напряжений. Четвертая теория прочности (энергетическая) — Теория наибольшей удельной потенциальной энергии формоизменения. Теория прочности Мора — Теория предельных напряжённых состояний (иногда говорят — V теория прочности). Из всех вышеперечисленных теорий прочности наиболее полной, точной и всеобъемлющей является теория Мора. Все её положения были проверены экспериментально. Она подходит как для проверки прочности хрупких материалов (чугун, бетон, кирпич), так и для проверки на прочность пластичных материалов (низкоуглеродистая сталь). Теория наибольших нормальных напряжений и теория наибольших деформаций подходит только для прочностного анализа хрупких материалов, причём только для каких-то определённых условий нагружения, если требовать повышенную точность расчёта. Вот поэтому первые две теории прочности сегодня применять не рекомендуется. Результаты теории наибольших касательных напряжений и теории наибольшей удельной потенциальной энергии формоизменения можно получить в некоторых частных случаях нагружения при применении теории Мора. |