Интеграционное правопонимание. Основные понятия и факты геометрии 79 классов

• Название: Основные понятия и факты геометрии 79 классов
• Анкор: Интеграционное правопонимание
• Дата: 14.02.2023
• Размер: 2.24 Mb.
• Имя файла: -1822024027.doc
• Тип: Документы; #936370
• страница: 4 из 8

Подобие треугольников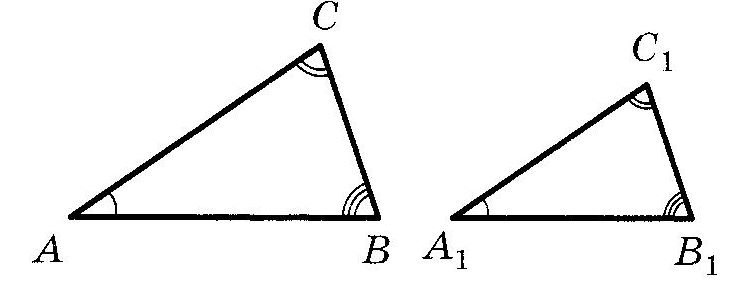

Опр. Два треугольника называются подобными, если:

1. 
   Их углы соответственно равны
   
2. 
   Их сходственные стороны пропорциональны.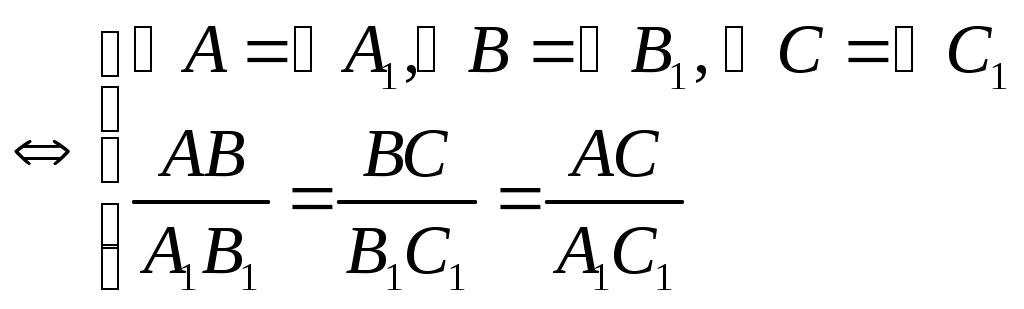
   



Опр. Отношение сходственных сторон подобных треугольников называется коэффициентом подобия.
Теорема (о периметрах подобных треугольников)

Периметры подобных треугольников относятся как коэффициент подобия.
Теорема (о площадях подобных треугольников)

Площади подобных треугольников относятся как коэффициент подобия в квадрате.
Признаки подобия треугольников

1. 
   Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники являются подобными.
   
2. 
   Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники являются подобными.
   
3. 
   Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники являются подобными.
   

4. Параллельные прямые

Опр. Две прямые на плоскости называются ПАРАЛЛЕЛЬНЫМИ, если они не пересекаются.
Аксиома параллельных (пятый постулат Евклида)

Через точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
Опр. Прямая называется СЕКУЩЕЙ для двух данных прямых, если она пересекает каждую из них.

Виды углов при пересечении прямых секущей




1 3 7 8
4 2 5 6


3 и 5, 2 и 7 - накрест лежащие

3 и 7, 2 и 5 - односторонние

1 и 7, 3 и 8, 4 и 5, 2 и 6 – соответственные
Теорема (Признаки параллельности прямых)

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые являются параллельными.

Если при пересечении двух прямых секущей соответственные углы равны, то прямые являются параллельными.

Если при пересечении двух прямых секущей сумма односторонних углов равна , то прямые являются параллельными.
Теорема (свойства углов при параллельных прямых)

Если две параллельные прямые пересечены секущей, то:

1. 
   Любая пара накрест лежащих углов равна
   
2. 
   Любая пара соответственных углов равна
   
3. 
   Сумма любой пары односторонних углов равна .