Интеграционное правопонимание. Основные понятия и факты геометрии 79 классов
 Скачать 2.24 Mb. Скачать 2.24 Mb.
|
3. ТреугольникиОпр. Треугольник называется прямоугольным, если у него есть прямой угол. Опр. Треугольник называется тупоугольным, если у него есть тупой угол. Опр. Треугольник называется остроугольным, если все его углы острые. Опр. Треугольник называется равнобедренным, если две его стороны равны. Опр. Треугольник называется правильным (равносторонним), если все его стороны равны. Опр. Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Опр. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. Опр. Высотой треугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из данной вершины к прямой, содержащей противоположную сторону. Равенство треугольниковОпр1. Два треугольника называются равными, если их можно совместить движением. (Л.С. Атанасян) Опр2. Два треугольника называются равными, если у них соответствующие стороны равны и соответствующие углы равны. (В.А. Погорелов) Пользуясь первым определением, можно доказать второе, и наоборот. Значит, эти определения равносильны. теорема (Признаки равенства треугольников), номера важно знать: 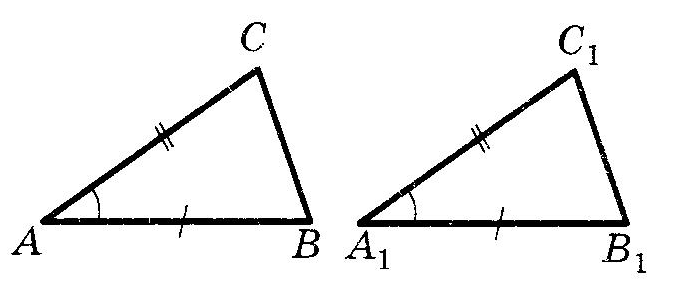 (По двум сторонам и углу) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. (По двум сторонам и углу) Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.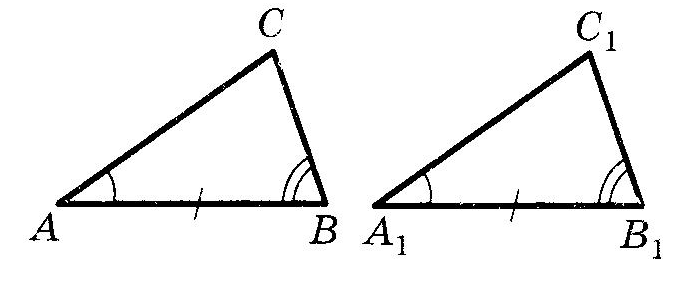 (По стороне и двум углам) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. (По стороне и двум углам) Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.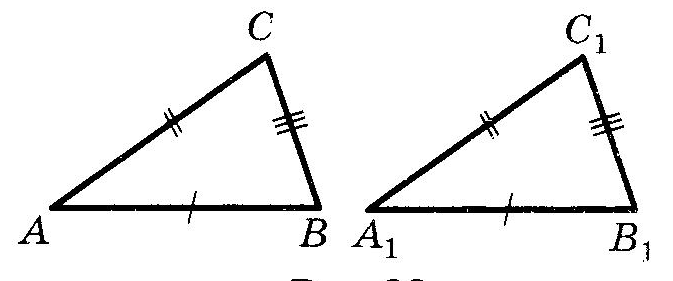 (По трем сторонам) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. (По трем сторонам) Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.Равнобедренный треугольникОпр. Треугольник называется равнобедренным, если две его стороны равны. Теорема (Свойство углов при основании равнобедренного треугольника) Углы при основании равнобедренного треугольника равны. Теорема (Свойство биссектрисы равнобедренного треугольника к основанию) Биссектриса равнобедренного треугольника, проведенная к его основанию, является медианой и высотой. Теорема (Признаки равнобедренного треугольника) Если в треугольники выполнено хоть одно из условий: два угла равны медиана совпала с высотой высота совпала с биссектрисой медиана совпала с биссектрисой, то такой треугольник является равнобедренным. Равенство равнобедренных треугольниковтеорема (Признаки равенства равнобедренных треугольников), номера не важны, наличие или отсутствие слова “соответственно” важно: (По боковой стороне и основанию) Если боковая сторона и основание одного равнобедренного треугольника соответственно равны боковой стороне и основанию другого равнобедренного треугольника, то такие треугольники равны. (По основанию и углу при основании) Если боковая сторона и угол при основании одного равнобедренного треугольника равны боковой стороне и углу при основании другого равнобедренного треугольника, то такие треугольники равны. (По боковой стороне и углу при вершине) Если боковая сторона и угол при вершине одного равнобедренного треугольника равны боковой стороне и углу при вершине другого равнобедренного треугольника, то такие треугольники равны. (По основанию и углу при вершине) Если основание и угол при вершине одного равнобедренного треугольника равны основанию и углу при вершине другого равнобедренного треугольника, то такие треугольники равны. (По боковой стороне и углу при основании) Если боковая сторона и угол при основании одного равнобедренного треугольника равны боковой стороне и углу при основании другого равнобедренного треугольника, то такие треугольники равны. |
