Интеграционное правопонимание. Основные понятия и факты геометрии 79 классов

• Название: Основные понятия и факты геометрии 79 классов
• Анкор: Интеграционное правопонимание
• Дата: 14.02.2023
• Размер: 2.24 Mb.
• Имя файла: -1822024027.doc
• Тип: Документы; #936370
• страница: 8 из 8

Вписанная и описанная окружности

Опр. Окружность называется ОПИСАННОЙ около треугольника, если она проходит через все его вершины.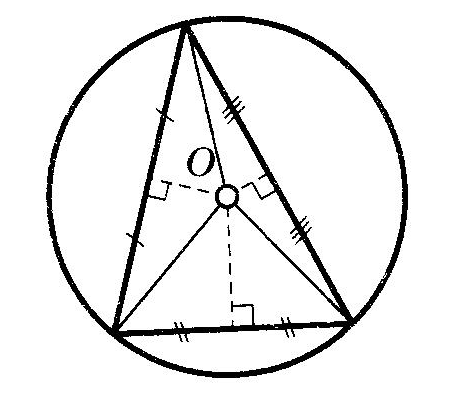
Теорема (о центре описанной окружности)

Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника.
Теорема (об описанной около треугольника окружности)

Около любого треугольника можно описать окружность и только одну.
Теорема (об описанной около четырехугольника окружности)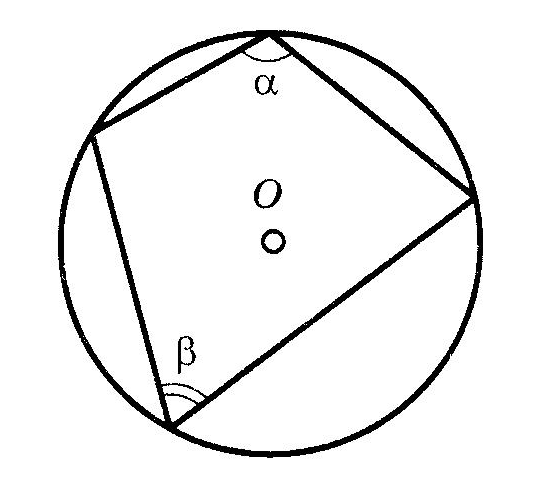

Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна .
Опр. Окружность называется ВПИСАННОЙ в треугольник, если она касается всех его сторон.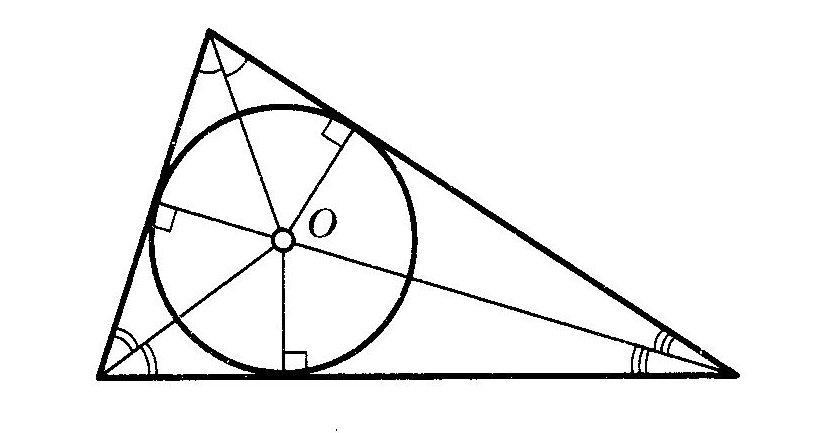
Теорема (о центре вписанной окружности)

Центр вписанной в треугольник окружности лежит на пересечении его биссектрис.

Теорема (о ВПИСАННОЙ В треугольника окружности)

В любой треугольник можно вписать окружность и только одну.
Теорема (о ВПИСАННОЙ В четырехугольник окружности)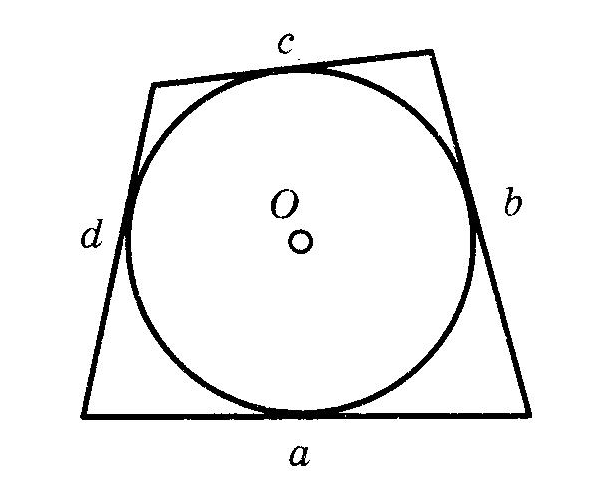

В четырехугольник можно вписать окружность тогда и только тогда, когда суммы противоположных сторон его равны.

Около параллелограмма может быть описана окружность тогда и только тогда, когда он является прямоугольником.

В параллелограмм может быть вписана окружность тогда и только тогда, когда он является ромбом.

Около трапеции можно описать окружность тогда и только тогда, когда она является равнобедренной.

10. Векторы

Опр. Вектором называется направленный отрезок.

Опр. Длиной (модулем) вектора АВ называется длина вектора АВ.

Опр. Векторы, лежащие на параллельных прямых или на одной прямой, называются коллинеарными векторами.

Коллинеарные векторы могут быть сонаправленными (они имеют одинаковые направления) и противоположно направленными (они имеют разные направления).

Опр. Векторы называются равными, если они сонаправлены и имеют одинаковые длины.

Действия над векторами

Можно сложить два вектора по правилу треугольника или правилу параллелограмма.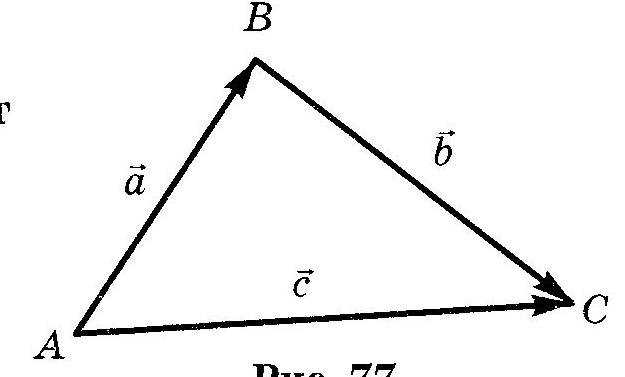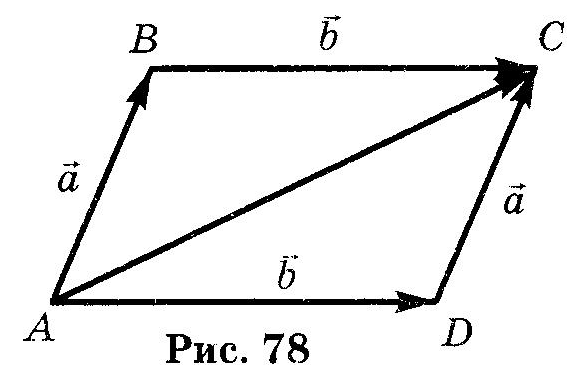



Свойства сложения векторов:

1 .

2 .
Опр. Произведением ненулевого вектора и числа k называется такой вектор , что:

1.

2. если

если .
Свойства умножения вектора на число ( и - числа)
1 . сочетательный закон

2 . первый распределительный закон

3 . второй распределительный закон

Опр. Координатами вектора называются коэффициенты его разложения по базисным векторам и .

Если , то .
ОСНОВНЫЕ ЗАДАЧИ В КООРДИНАТАХ

1. Координаты вектора

Если точки имеют координаты M(x₁;y₁) N(x₂;y₂), то

вектор имеет координаты “конец минус начало”

2. Длина вектора

Если вектор имеет координаты p{x₁;y₁}, то

длина вектора равна |p|= .

3. Координаты cередины отрезка
Если точки имеют координаты M(x₁;y₁) N(x₂;y₂), то

середина отрезка имеект координаты Р

4. Расстояние между точками
Если точки имеют координаты M(x₁;y₁) N(x₂;y₂), то

Уравнение окружности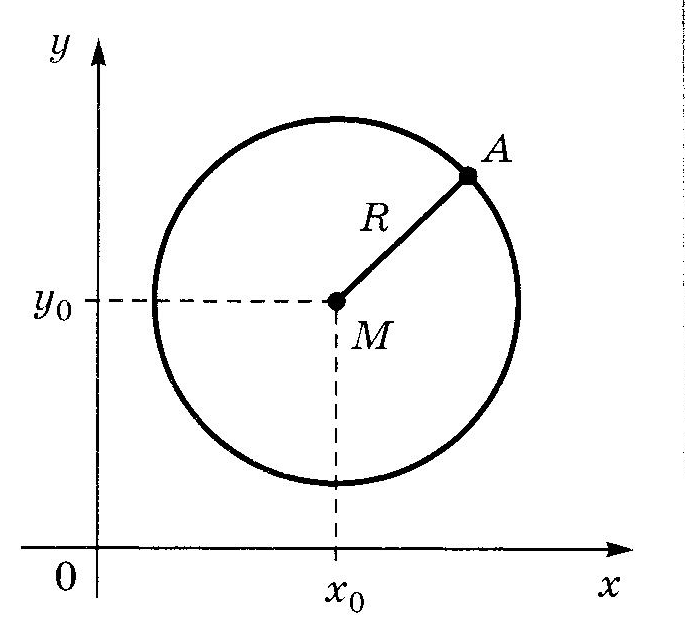

В прямоугольной системе координат уравнение окружности с центром в точке и радиуса R имеет вид:
Уравнение прямой
В прямоугольной системе координат уравнение прямой имеет вид Ах+Ву+С=0

Уравнение горизонтальной прямой имеет вид у=с, где с - число.

Уравнение оси абсцисс имеет вид у=0.

Уравнение вертикальной прямой имеет вид х=с, где с - число.

Уравнение оси ординат имеет вид х=0.

Скалярное произведение векторов

Опр. 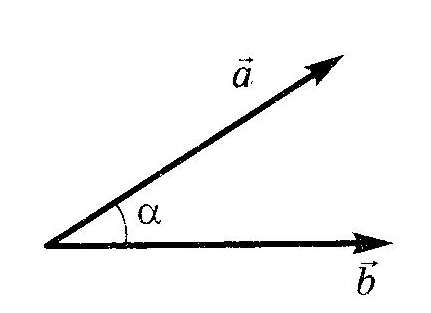Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними
Свойства скалярного произведения векторов
1 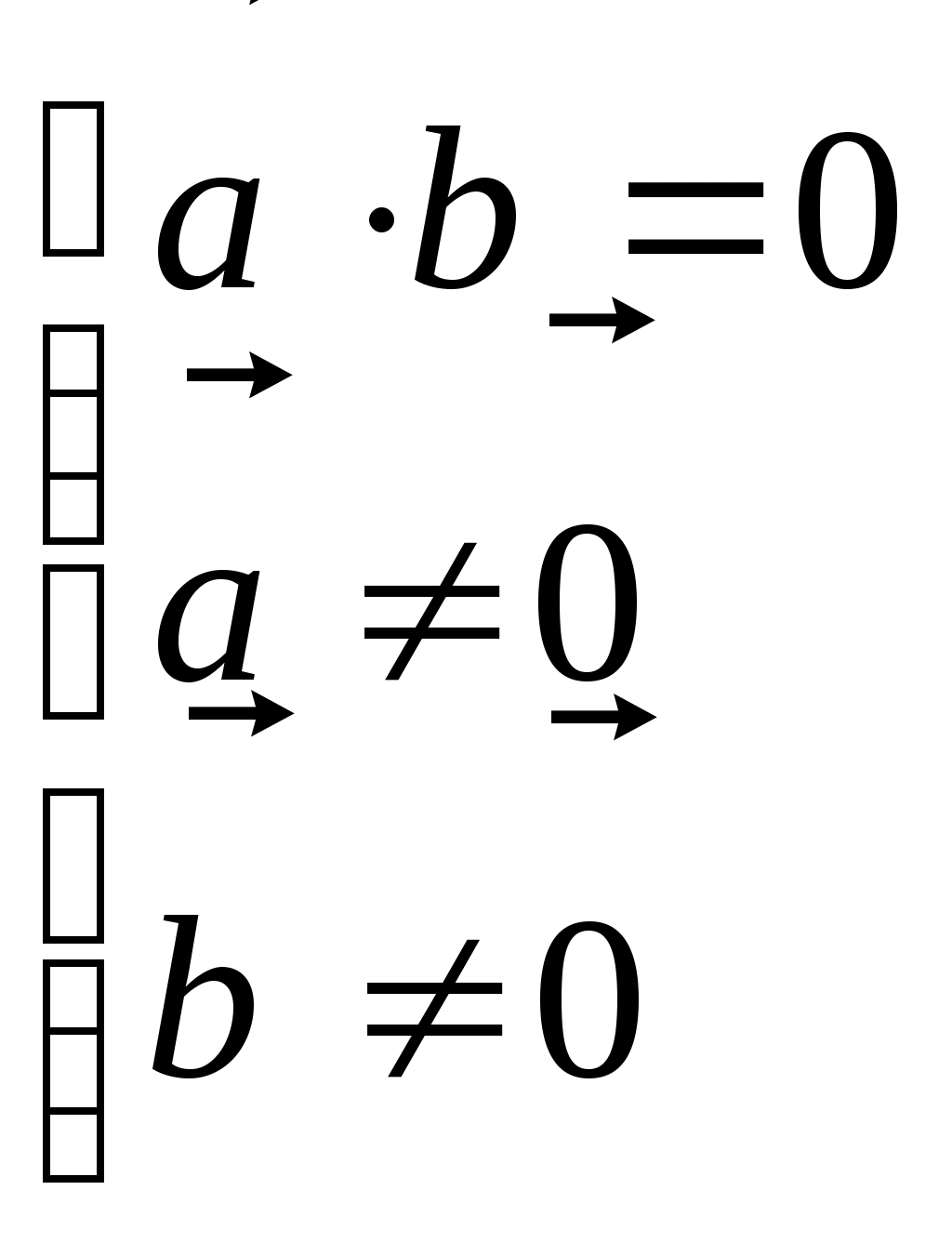. Если векторы перпендикулярны, то их скалярное произведение равно нулю.



2 . Если скалярное произведение двух ненулевых векторов равно нулю, то эти векторы перпендикулярны.



3 . Скалярный квадрат вектора равен квадрату его длины.


Теорема (скалярное произведение в координатах)

В прямоугольной системе координат скалярное произведение векторов и выражается формулой .
Следствия теоремы

1. 
   Ненулевые векторы и перпендикулярны тогда и только тогда, когда .
   
2. 
   Косинус угла 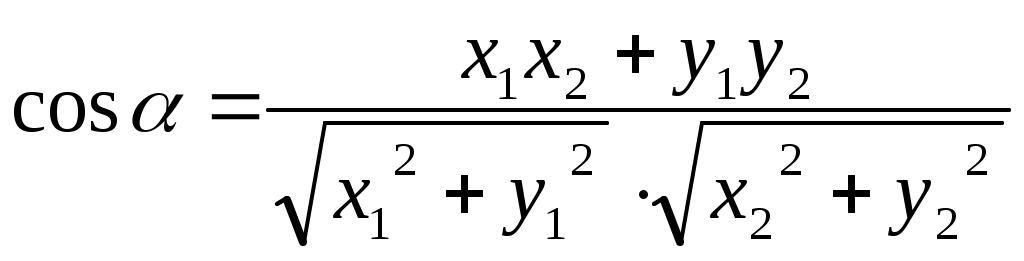между векторами и выражается формулой
   

Свойства скалярного произведения векторов
1 .

2 . переместительный закон

3 . распределительный закон

4 . сочетательный закон

11. Правильные многоугольники

Опр. Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.

Формула для вычисления угла правильного n-угольника .
Теорема (об окружности, описанной около правильного многоугольника)

Около любого правильного многоугольника можно описать окружность, и притом только одну.
Теорема (об окружности, вписанной в правильный многоугольник)

В любой правильный многоугольник можно вписать окружность, и притом только одну.

Следствия теоремы

1. 
   центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.
   
2. 
   Окружность, вписанная в правильный многоугольник, касается его сторон в их серединах.
   

Формула для вычисления стороны правильного n-угольника .

Формула для вычисления радиуса вписанной окружности правильного n-угольника .

Формула длины окружности

Формула площади круга

Опр. Сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Формула площади сектора

Опр. Сегментом называется часть круга, ограниченная дугой окружности и хордой, соединяющей концы этой дуги.

Формула площади сегмента

12. Теоремы Чевы и Менелая

теорема чевы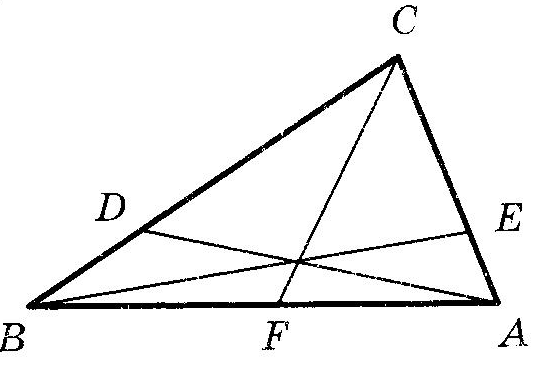

Если точки , , лежат на сторонах , , соответственно, то отрезки , и пересекаются в одной точке тогда и только тогда, когда (критерий того, что отрезки , и пересекаются в одной точке).

Теорема менелая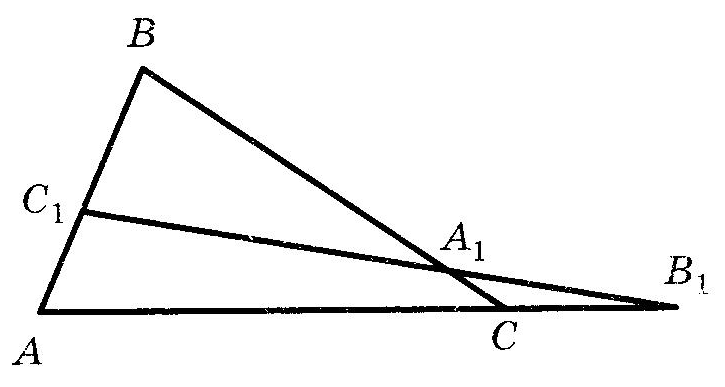

Прямая пересекает произвольный треугольник , причем - точка её пересечения со стороной , - точка её пересечения со стороной ВС и - точка её пересечения с продолжением стороны , тогда и только тогда, когда (критерий того, что точки , , лежат на одной прямой).

1 В учебнике Л.С. Атанасяна другая система аксиом. Эти две системы аксиом не противоречат друг другу.