Интеграционное правопонимание. Основные понятия и факты геометрии 79 классов

• Название: Основные понятия и факты геометрии 79 классов
• Анкор: Интеграционное правопонимание
• Дата: 14.02.2023
• Размер: 2.24 Mb.
• Имя файла: -1822024027.doc
• Тип: Документы; #936370
• страница: 7 из 8

9. Окружность

Опр. РАССТОЯНИЕМ от точки до прямой называется длина перпендикуляра, опущенного из данной точки на данную прямую.
Опр. ОКРУЖНОСТЬЮ называется множество всех точек плоскости, равноудаленных от данной точки.
Опр. ХОРДОЙ окружности называется отрезок, концы которого лежат на этой окружности.
Опр. ДИАМЕТРОМ окружности называется хорда, проходящая через её центр.

Взаимное расположение прямой и окружности

Опр. КАСАТЕЛЬНОЙ к окружности называется прямая, имеющая с этой окружностью одну общую точку.
Теорема (свойство касательной)

Касательная к окружности перпендикулярна радиусу этой окружности, проведенному в точку касания.
Теорема (признак касательной)

Если прямая проходит через конец радиуса, лежащий на окружности, перпендикулярно ему, то она является касательной к этой окружности.
Теорема (об отрезках касательных)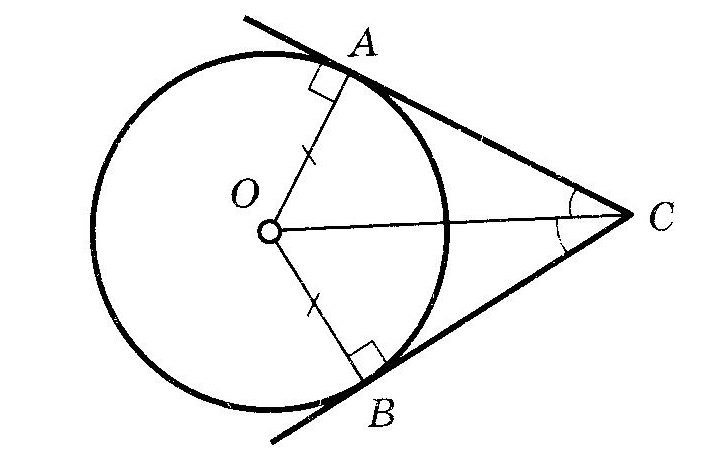

Отрезки касательных, проведенных к окружности из одной точки, равны и образуют равные углы с прямой, соединяющей эту точку с центром окружности.

Углы и окружность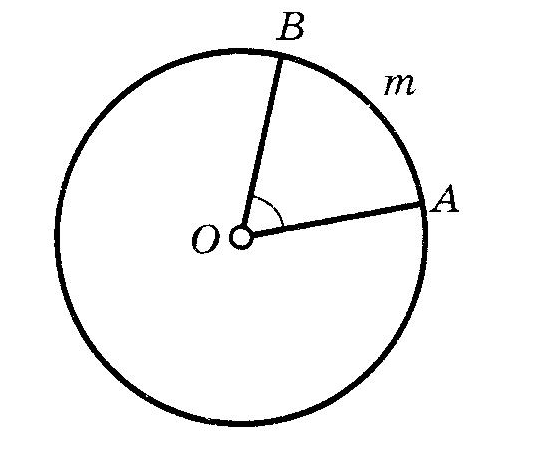

если дуга АВ окружности с центром в точке О меньше половины окружности или является половиной окружности, то её градусная мера считается равной градусной мере центрального угла АОВ. Если же дуга АВ больше половины окружности, то её градусная мера считается равной .

1. Теорема о вписанном угле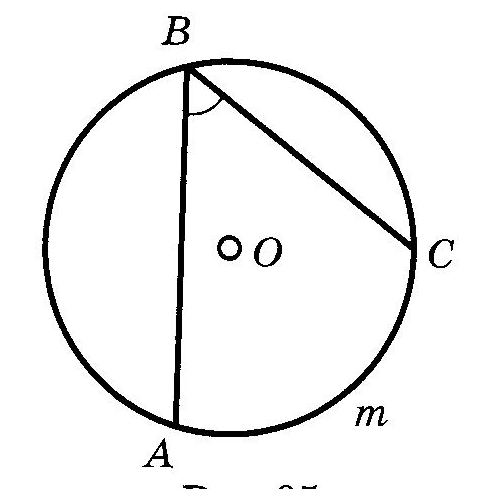
Вписанный угол измеряется половиной дуги, на которую он опирается.


Следствия теоремы о вписанном угле

1. 
   Вписанные углы, опирающиеся на одну дугу, равны.
   
2. 
   Вписанный угол, опирающийся на диаметр, прямой.
   

2. Угол между хордой и касательной измеряется половиной дуги, заключенной внутри него.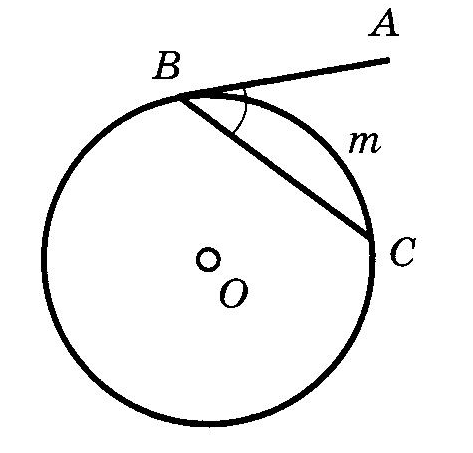


3. Угол между двумя касательными измеряется полуразностью дуг.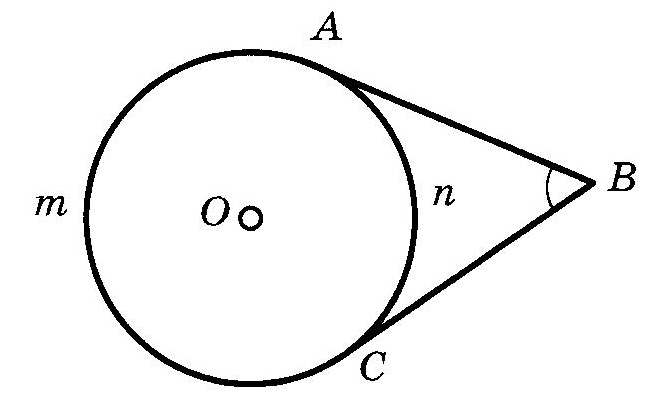


4. Угол между двумя хордами измеряется полусуммой дуг, на которые он опирается.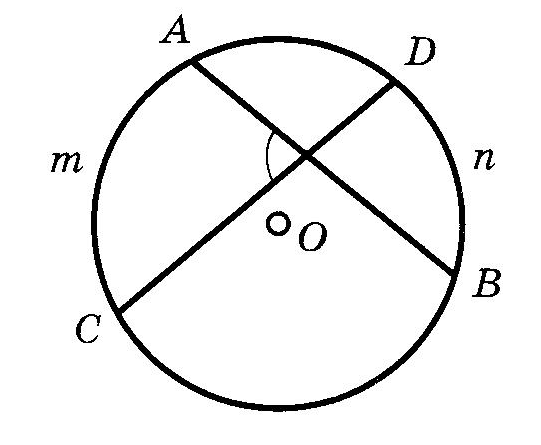


5. Угол между секущими измеряется полуразностью дуг между ними.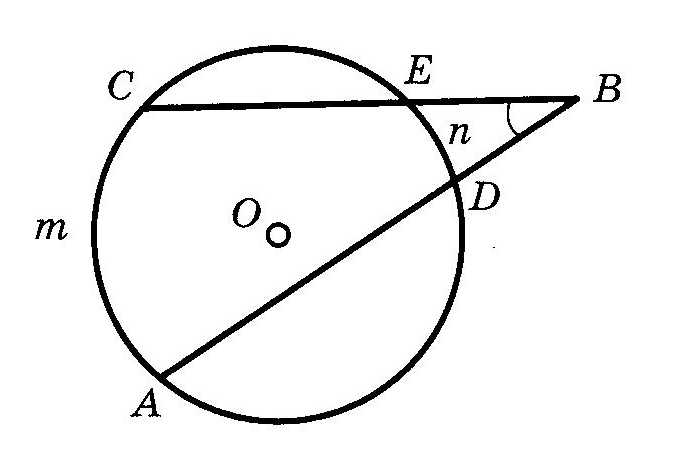


6. Угол между касательной и секущей измеряется полуразностью отсекаемых ими дуг, прилежащих к касательной.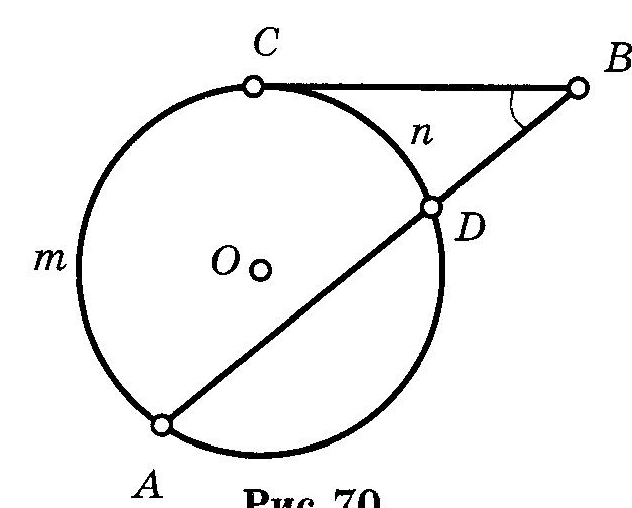

Отрезки и окружность

1. Теоремы (о хордах в окружности)

1. 
   Диаметр, перпендикулярный хорде, делит её пополам.
   
2. 
   Диаметр, делящий хорду пополам, перпендикулярен ей.
   
3. 
   Равные хорды равноудалены от центра.
   
4. 
   Равноудаленные от центра хорды равны.
   

2 . С
А E В

D

Если хорды АВ и СD пересекаются в точке Е, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
В

D

Е

А
3.

С

Если из одной точки В к окружности проведены две секущие BDA и BEC, то






4.

C


A D В
Теорема (о квадрате касательной)

Если через точку вне окружности проведены касательная и секущая к этой окружности, то квадрат касательной равен произведению внешней части секущей на всю секущую.