Опр. Геометрическим местом точек ГМТ называется множество всех точек плоскости, обладающих определенным свойством.
ГМТ, равноудаленных от данных точек А и В, есть серединный перпендикуляр к отрезку АВ.
ГМТ внутренних точек угла, равноудаленных от его сторон, есть биссектриса этого угла.
6. Четыреухугольники Параллелограмм
Опр. Параллелограммом называется четырехугольник, стороны которого попарно параллельны.
Свойства параллелограмма
1 . В параллелограмме противоположные стороны равны и противоположные углы равны. . В параллелограмме противоположные стороны равны и противоположные углы равны.
2 . Диагонали параллелограмма точкой пересечения делятся пополам. . Диагонали параллелограмма точкой пересечения делятся пополам.
Признаки параллелограмма
Если две стороны четырехугольника равны и параллельны, то этот четырехугольник является параллелограммом.
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник является параллелограммом.
Если диагонали четырехугольника точкой пересечения делятся пополам, то этот четырехугольник является параллелограммом.
В параллелограмме 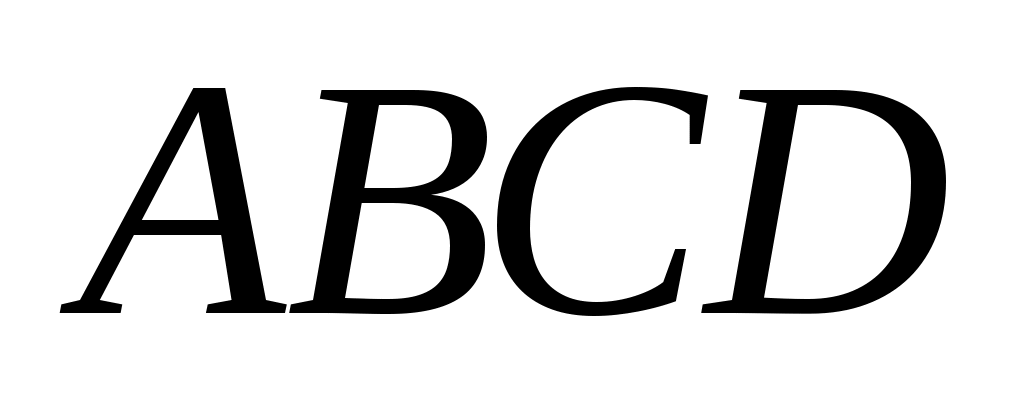 сумма квадратов его диагоналей равна сумме квадратов всех его сторон сумма квадратов его диагоналей равна сумме квадратов всех его сторон 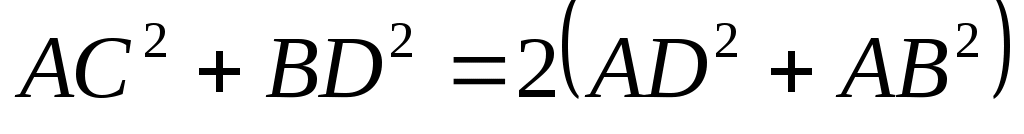
Теорема Фалеса
Если на одной из двух прямых отложить последовательно несколько равных между собой отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Теорема (о пропорциональных отрезках, обобщение теоремы Фалеса)
Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой отрезки, пропорциональные отрезкам на первой прямой.
Прямоугольник. Ромб. Квадрат
Опр. Прямоугольником называется параллелограмм, все углы которого прямые.
Специальное свойство прямоугольника
Диагонали прямоугольника равны.
Признак прямоугольника
Если диагонали параллелограмма равны, то он является прямоугольником.
Опр. Ромбом называется параллелограмм, все стороны которого равны.
Специальное свойство ромба
Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Признаки ромба
Если диагонали параллелограмма перпендикулярны, то он явлчяется ромбом.
Если диагональ параллелограмма делит его угол пополам, то он ялвется ромбом.
Опр. Квадратом называется прямоугольник, все стороны которого равны.
Трапеция
Опр. Четырехугольник называется трапецией, если две стороны его параллельны, а две другие – нет.
Параллельные стороны трапеции – основания
непараллельные стороны трапеции - боковые стороны
Опр. Трапеция назывется прямоугольной, если у нее есть прямой угол.
Опр. Трапеция называется равнобедренной, если ее боковые стороны равны.
Свойства равнобедренной трапеции
1 . Углы при каждом основании равнобедренной трапеции равны. . Углы при каждом основании равнобедренной трапеции равны.
2 .Диагонали равнобедренной трапеции равны. .Диагонали равнобедренной трапеции равны.
Признаки равнобедренной трапеции
Если углы при основании трапеции равны, то она является равнобедренной.
Если диагонали трапеции равны, то она является равнобедренной.
Теорема (о средней линии трапеции)
Средняя линия трапеции параллельна ее основаниям и равна их полусумме.
7. Площадь фигур
Свойства площадей
1 . Площадь каждой фигуры выражается положительным числом. . Площадь каждой фигуры выражается положительным числом.
2 . Равные многоугольники имеют равные площади. . Равные многоугольники имеют равные площади.
Фигуры, имеющие равные площади, называются равновеликими. Равные фигуры равновелики, но не всегда равновеликие фигуры равны.
3 . Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников. . Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
4 . Площадь квадрата равна квадрату его стороны. . Площадь квадрата равна квадрату его стороны.
Формулы площадей
1. Площадь квадрата 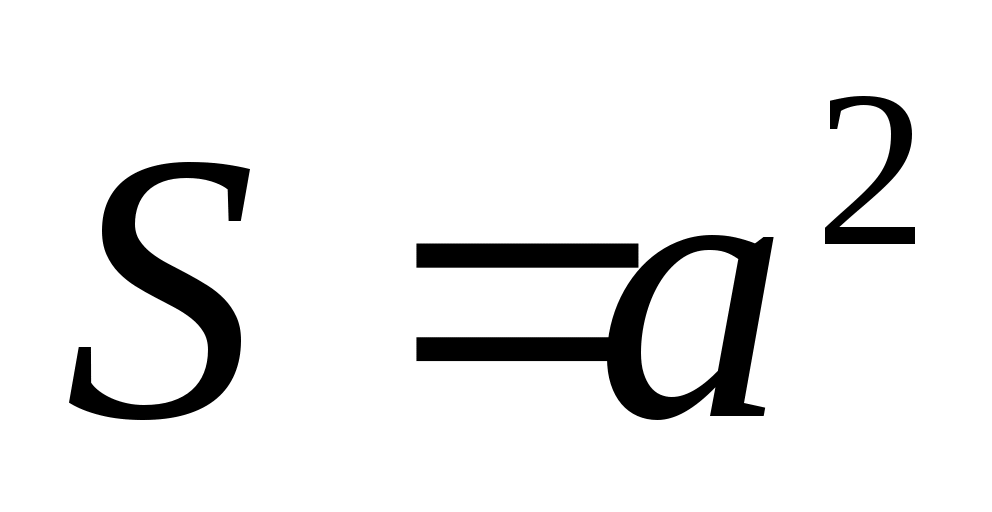 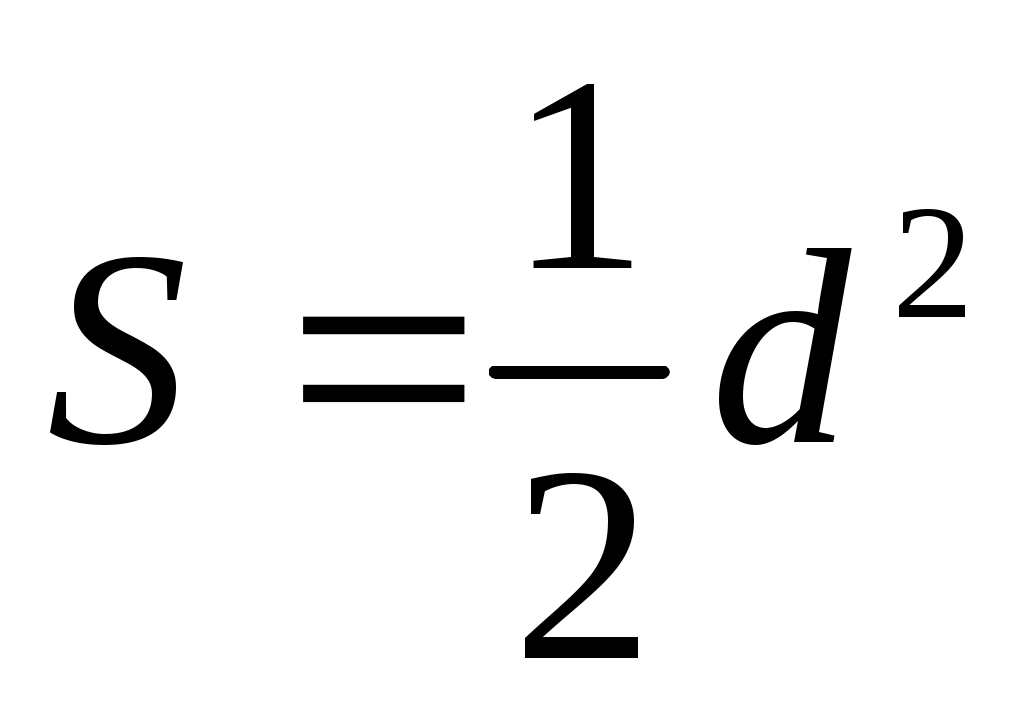
2. Площадь прямоугольника 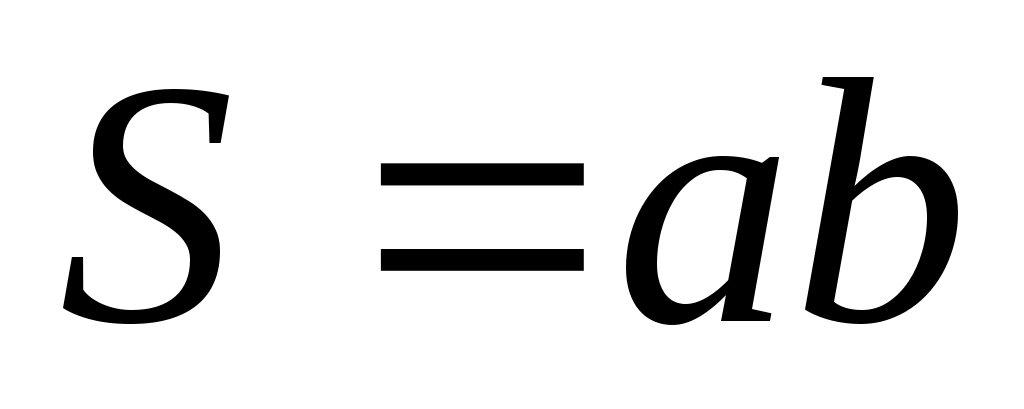 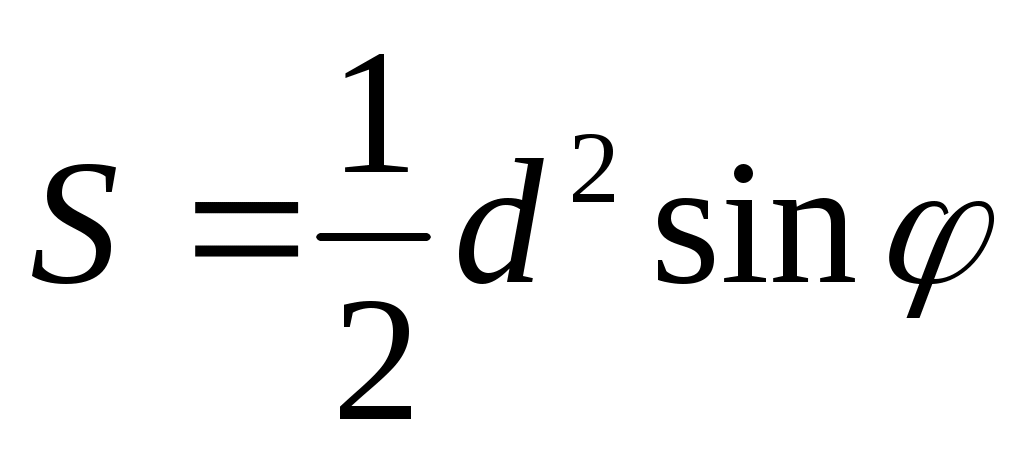 , где , где 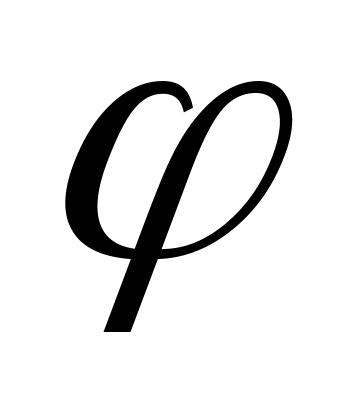 - угол между диагоналями. - угол между диагоналями.
3. Площадь треугольника
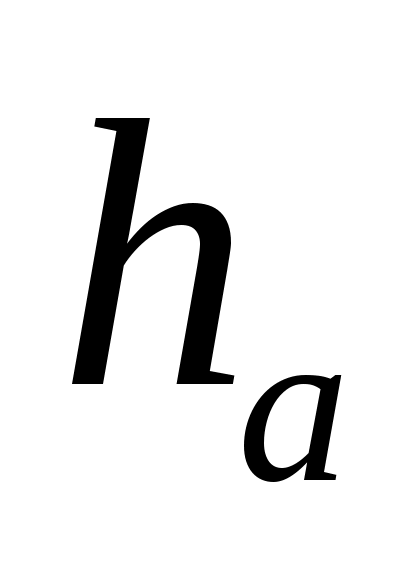 - высота к стороне - высота к стороне  , ,
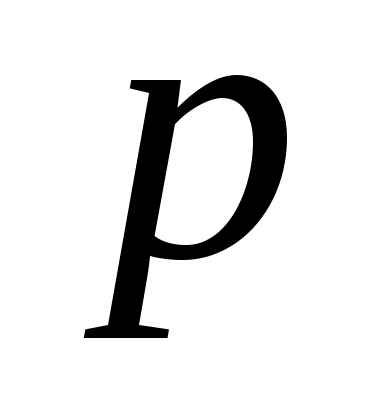 - полупериметр, - полупериметр,
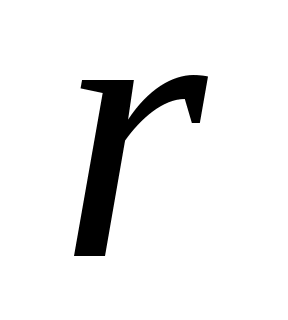 - радиус вписанной в треугольник окружности, - радиус вписанной в треугольник окружности,
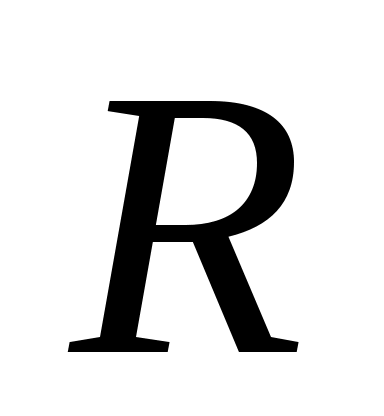 - радиус описанной около треугольника окружности - радиус описанной около треугольника окружности
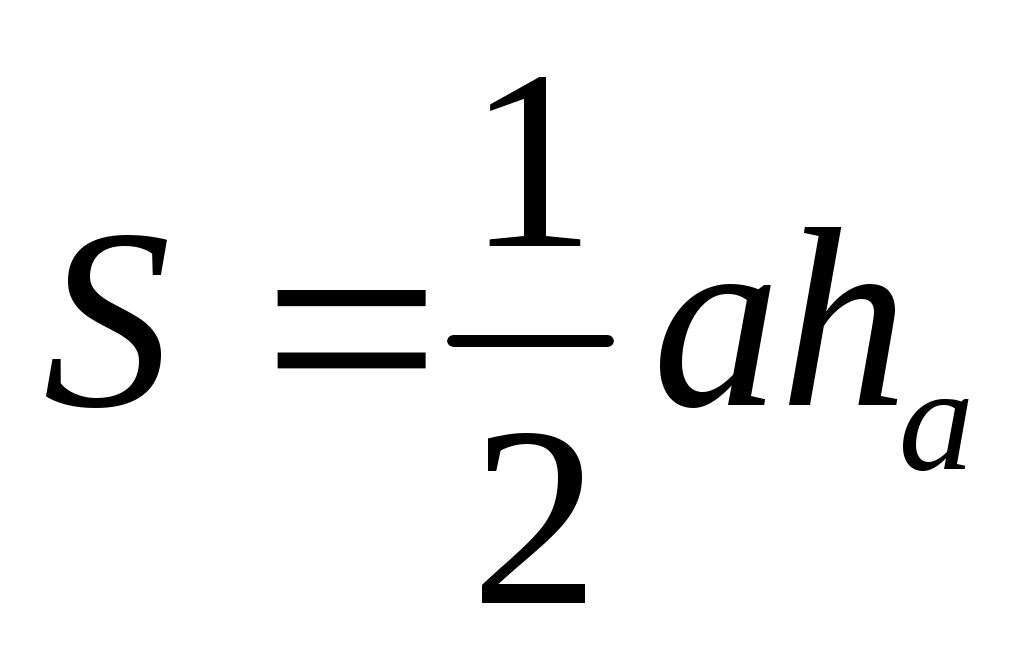
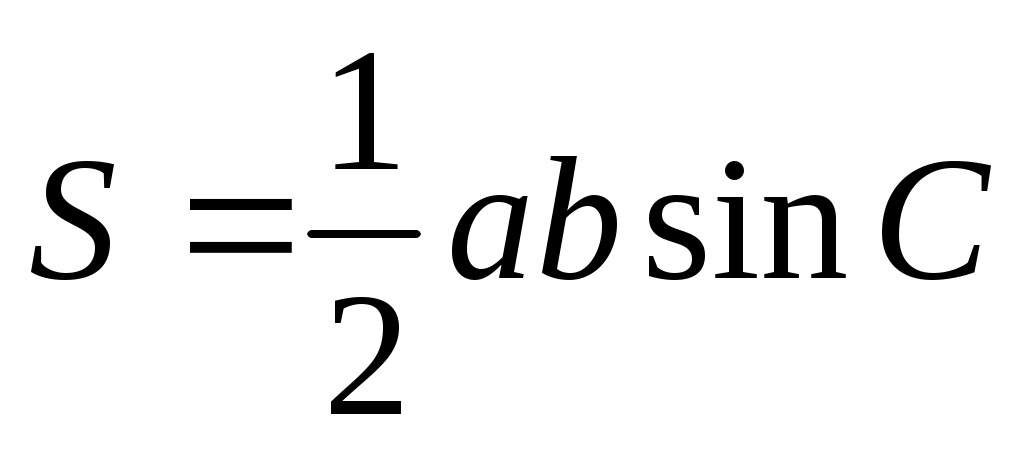
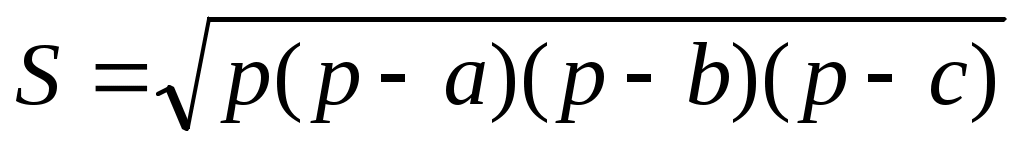 формула Герона формула Герона
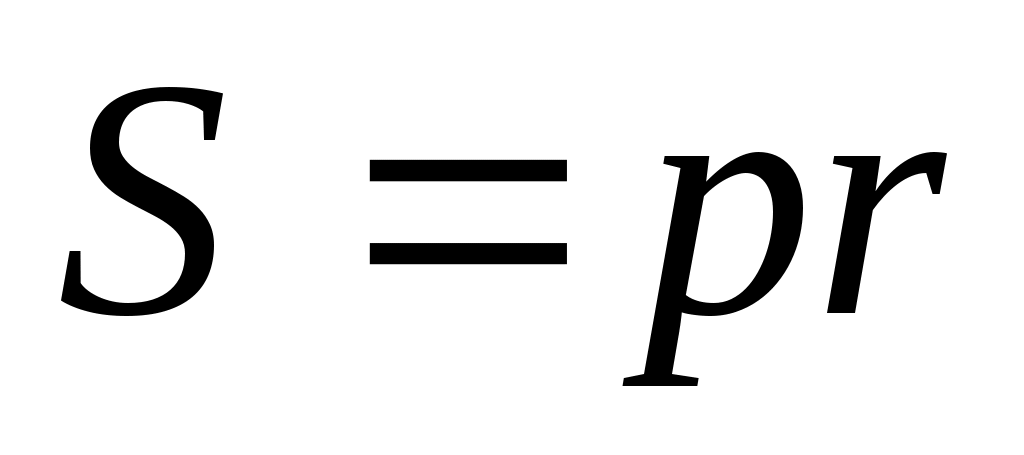
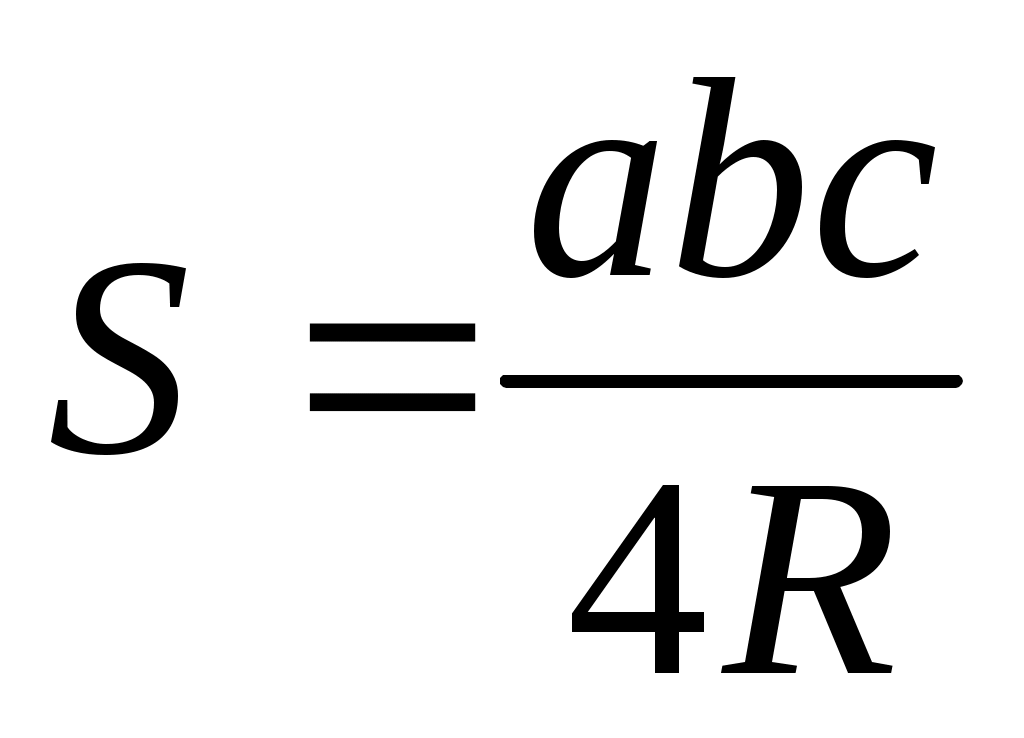
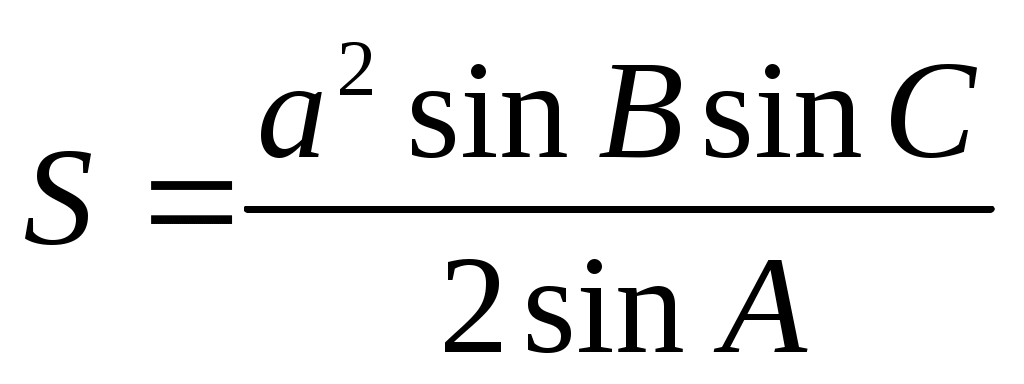
Если в треугольника 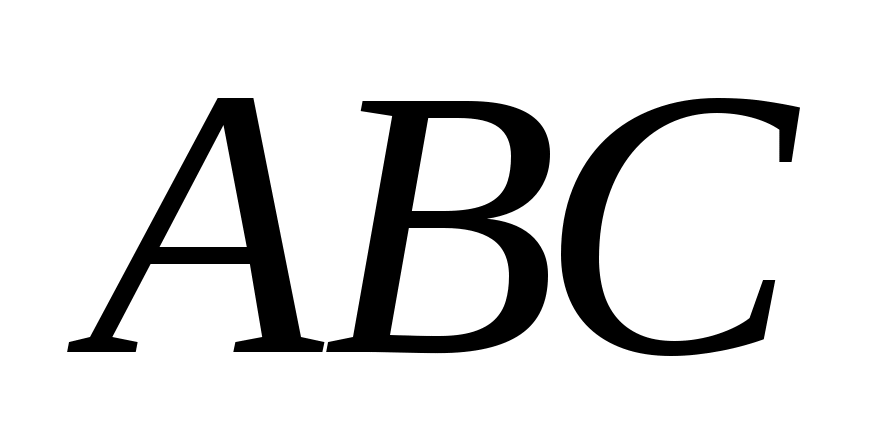 и и 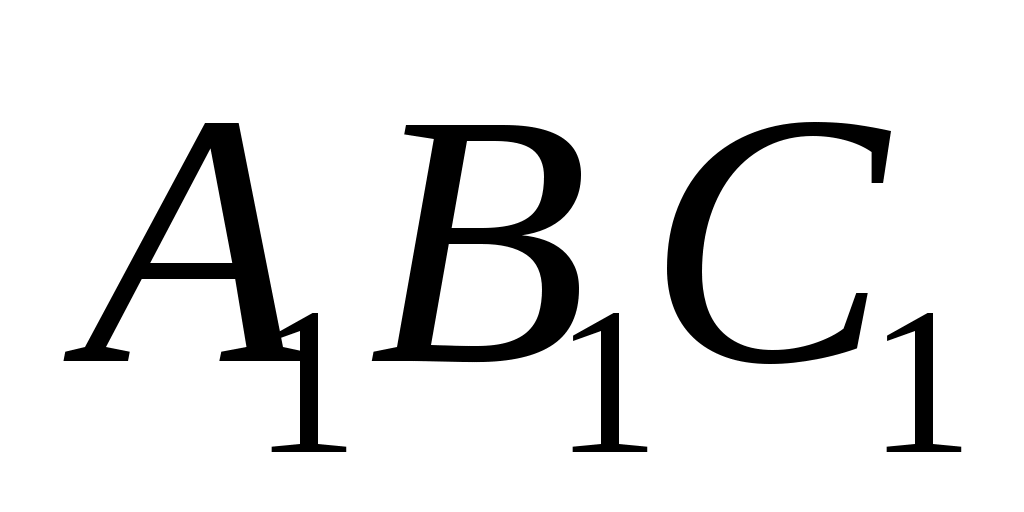 равны углы, то их площади относятся как произведения сторон, заключающих равные углы: если равны углы, то их площади относятся как произведения сторон, заключающих равные углы: если 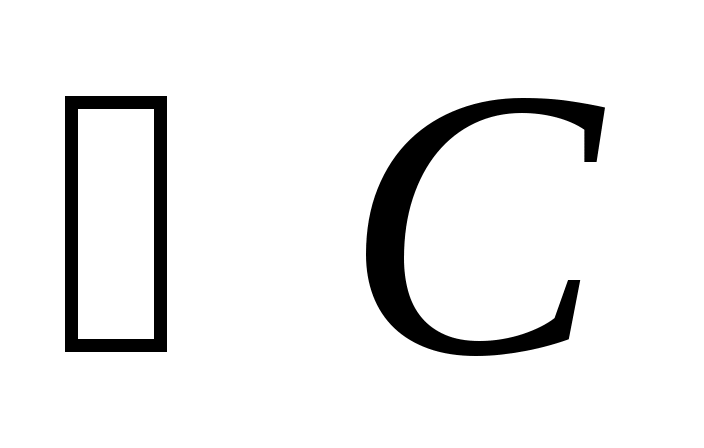 = =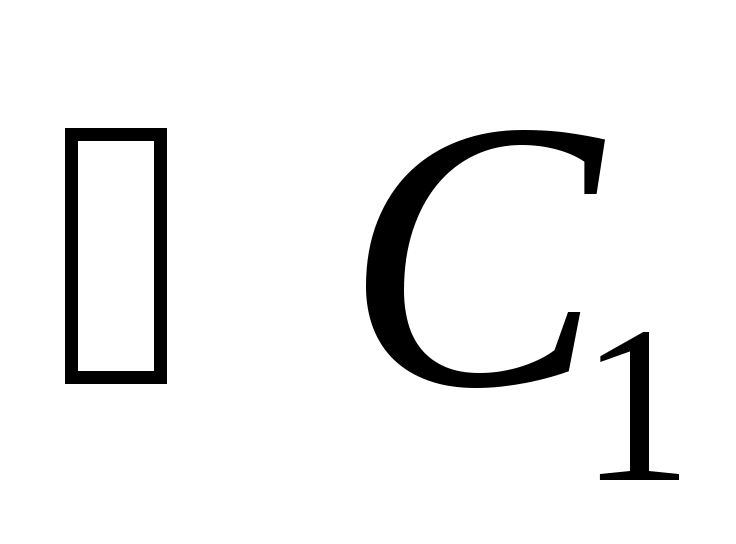 , то , то 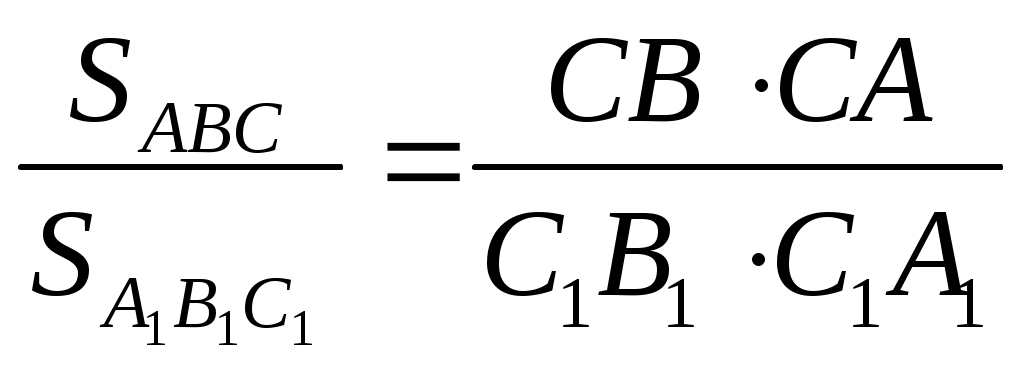
Если в треугольника 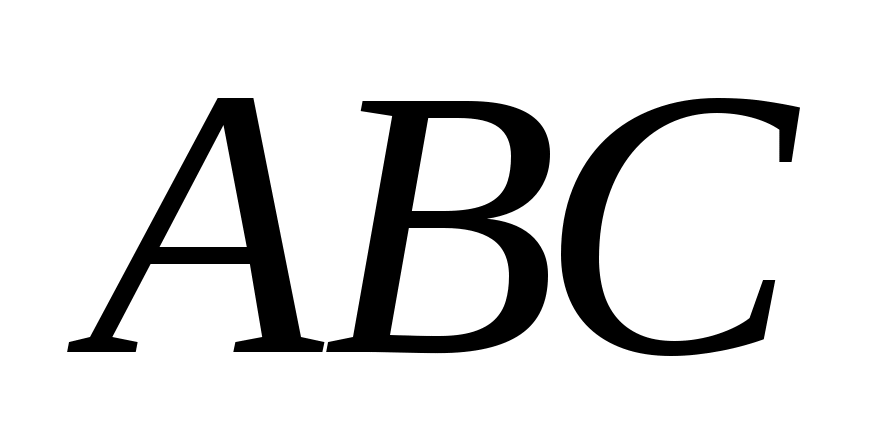 и и 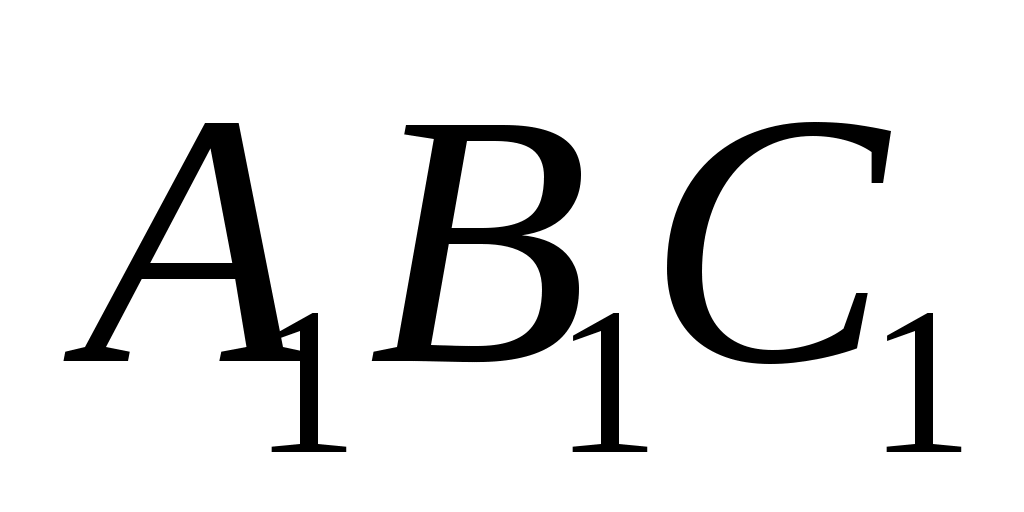 равны высоты, то их площади относятся как основания, к которым эти высоты проведены: если равны высоты, то их площади относятся как основания, к которым эти высоты проведены: если 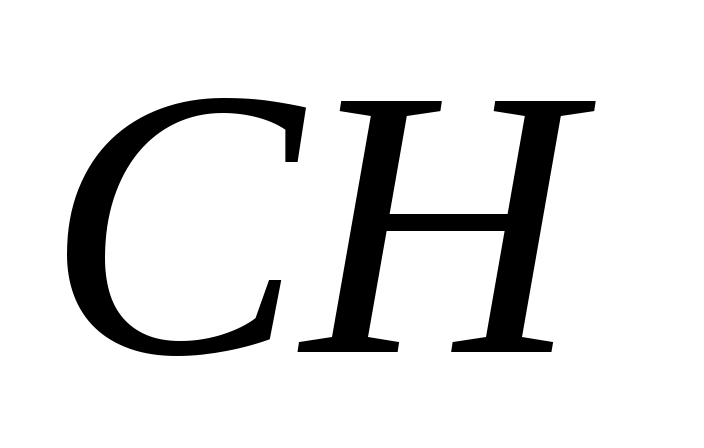 = =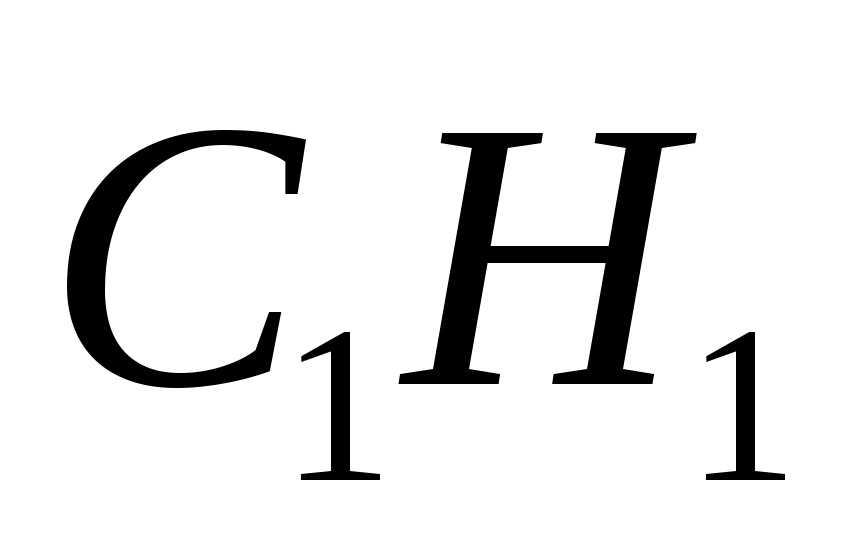 , то , то 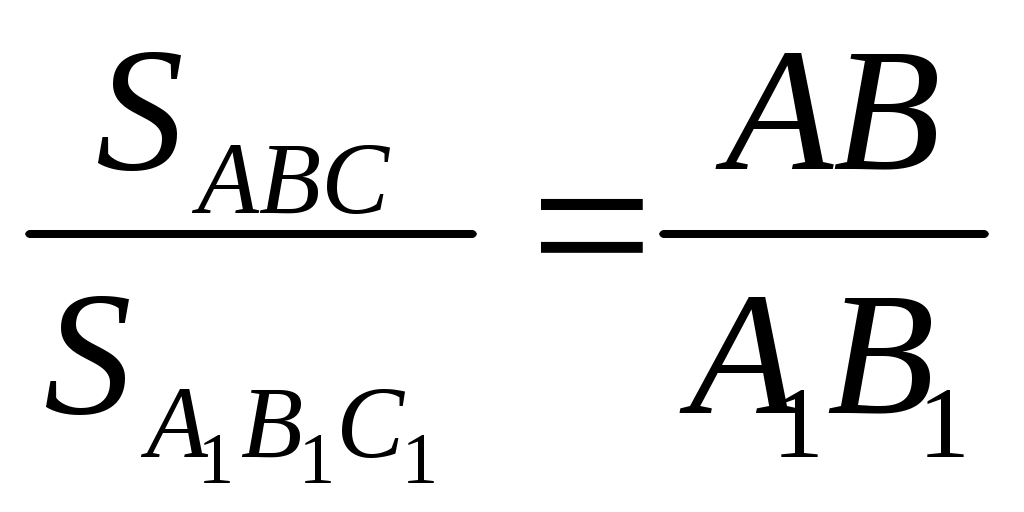
Если треугольники 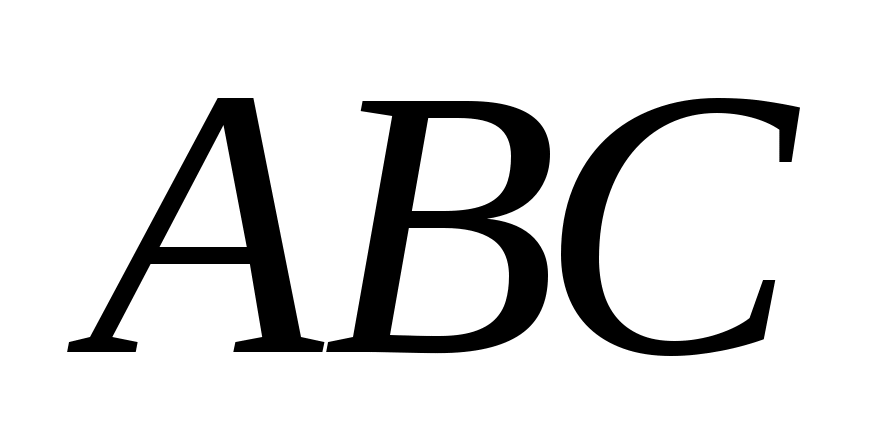 и и 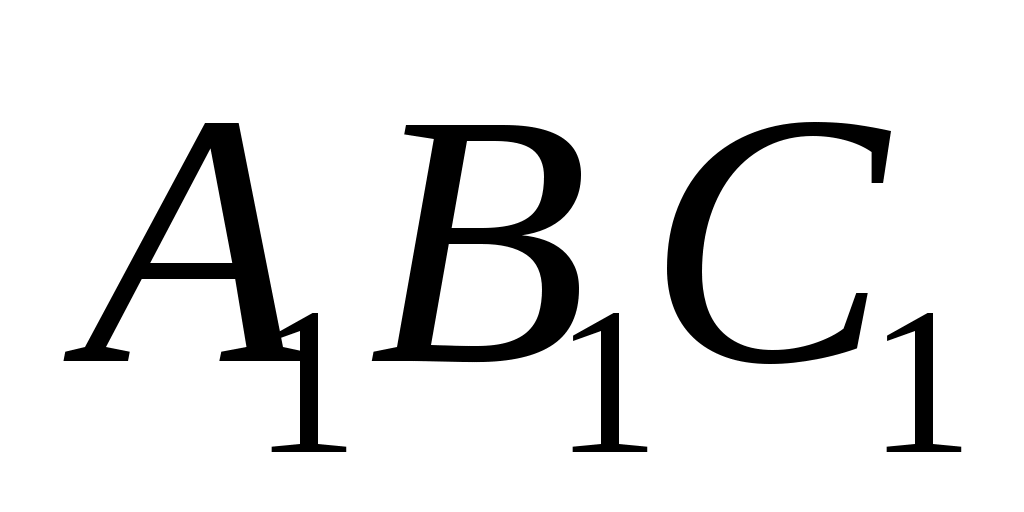 подобны, то их площади относятся как коэффициент подобия в квадрате: если подобны, то их площади относятся как коэффициент подобия в квадрате: если 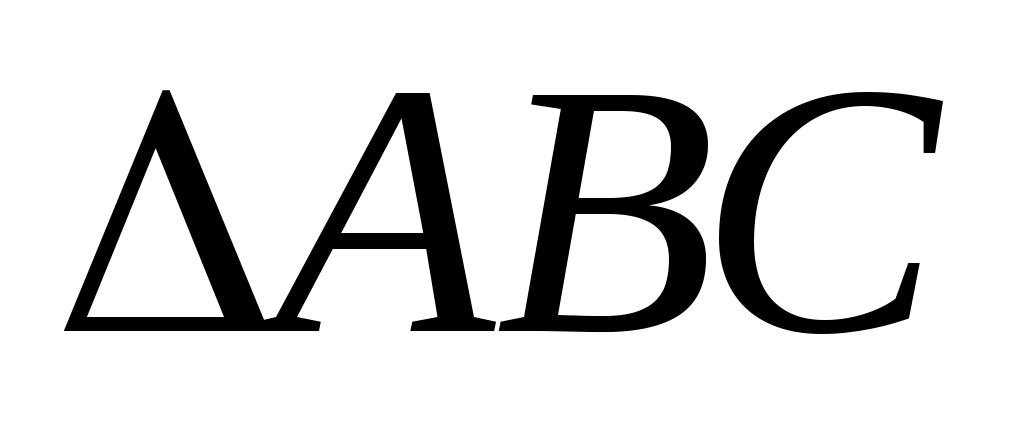 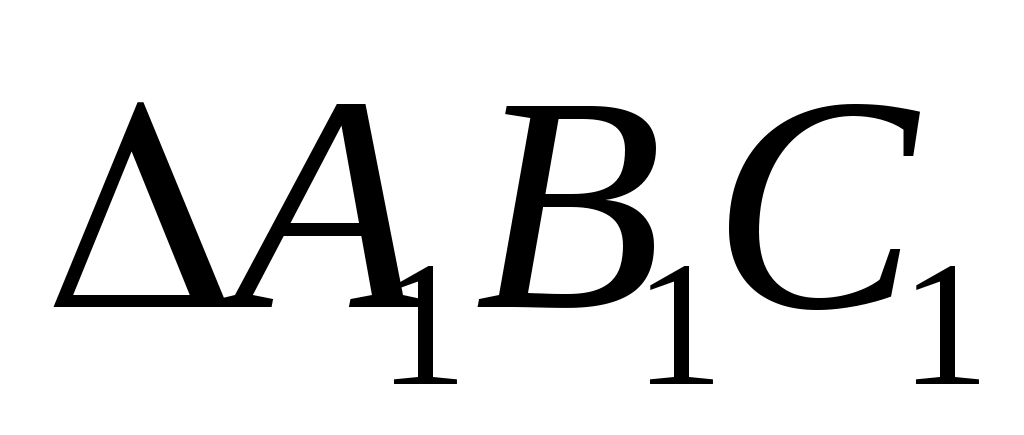 , то , то 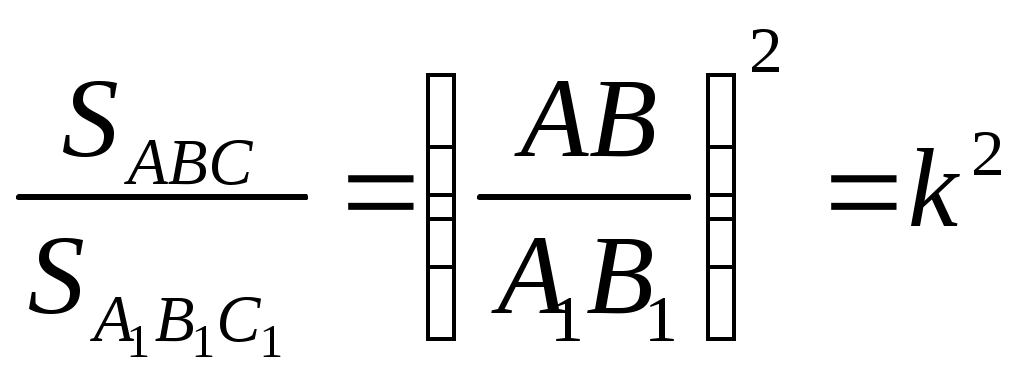 . .
4. 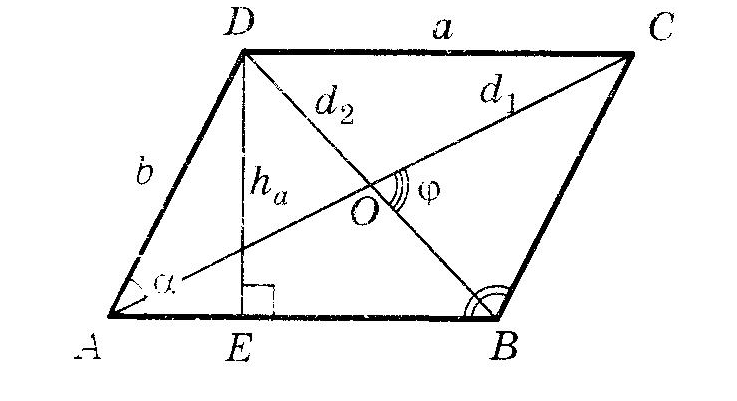 Площадь параллелограмма Площадь параллелограмма
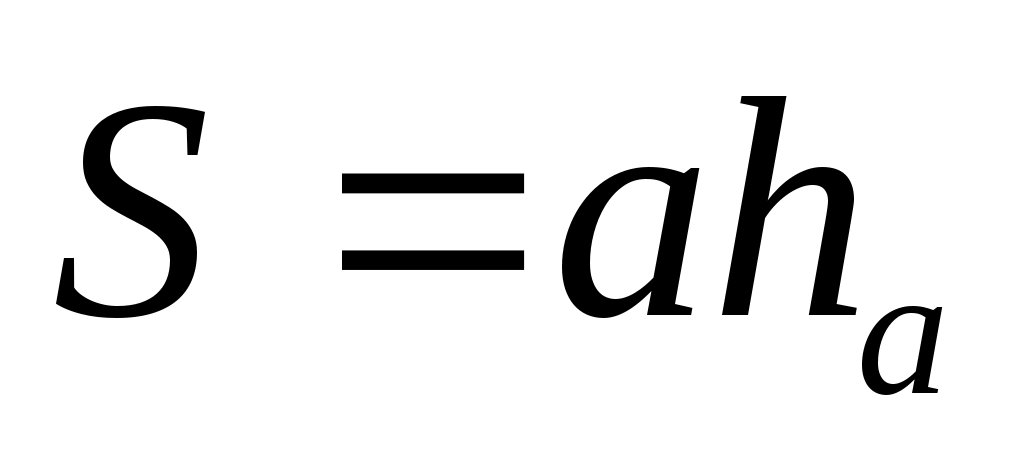 произведение стороны на высоту к ней произведение стороны на высоту к ней
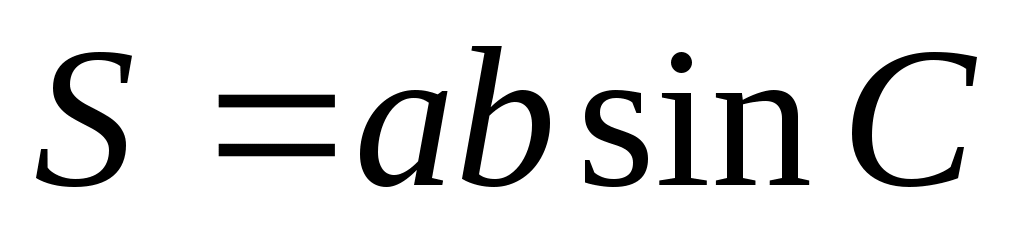 произведение двух сторон на синус угла между ними произведение двух сторон на синус угла между ними
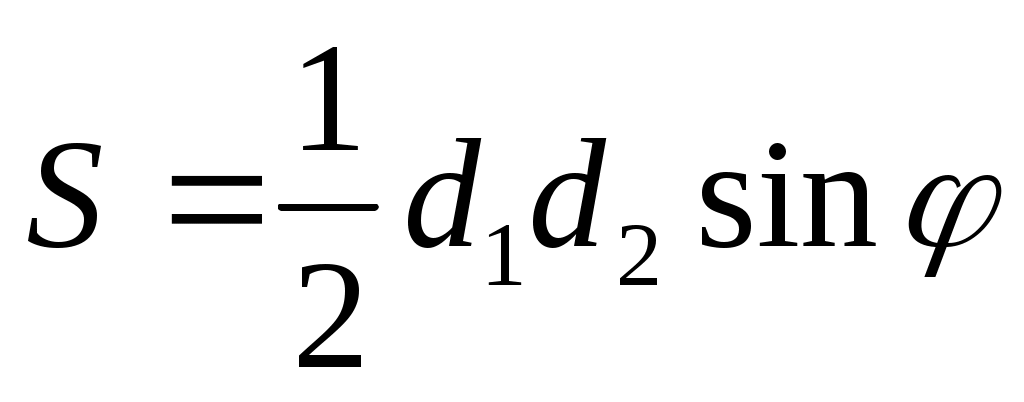 половина произведения двух диагоналей на синус угла между ними половина произведения двух диагоналей на синус угла между ними
5. Площадь ромба
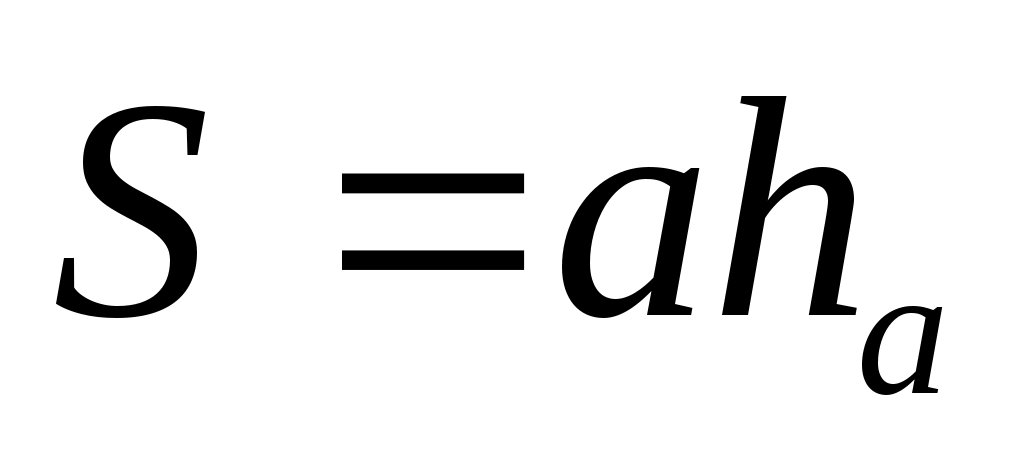 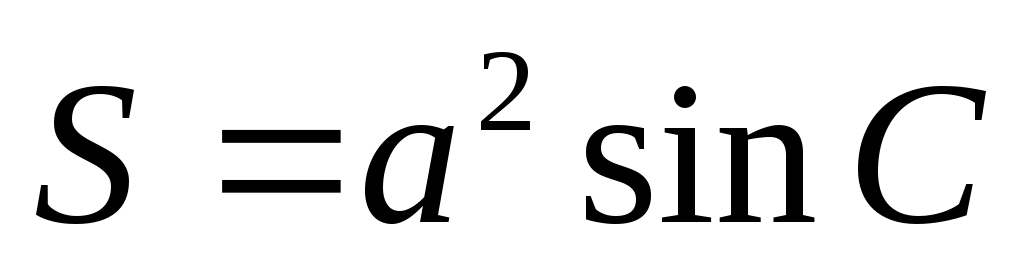 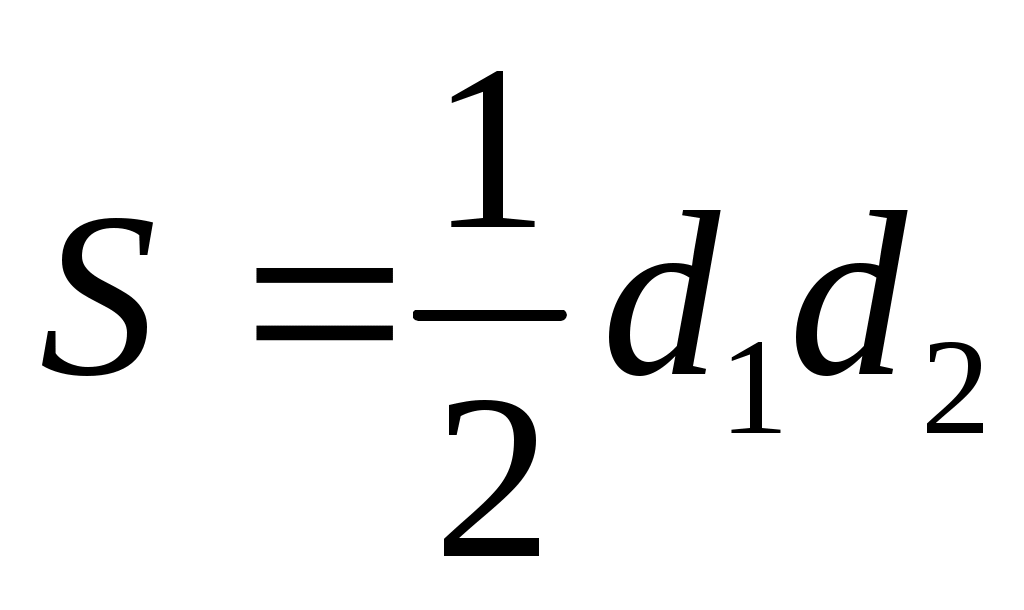
6. 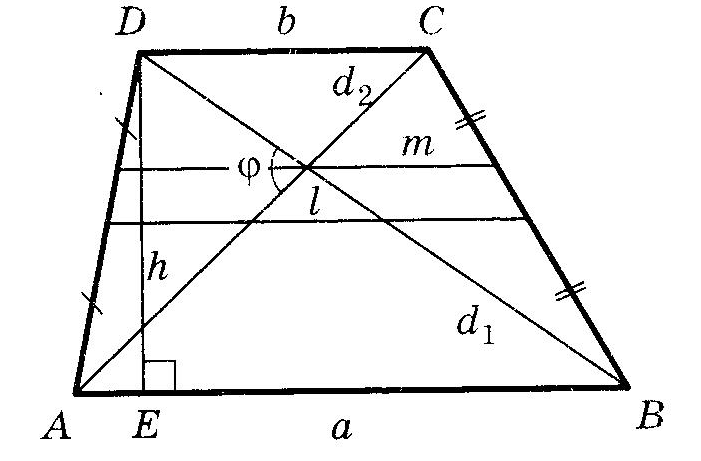 Площадь трапеции Площадь трапеции
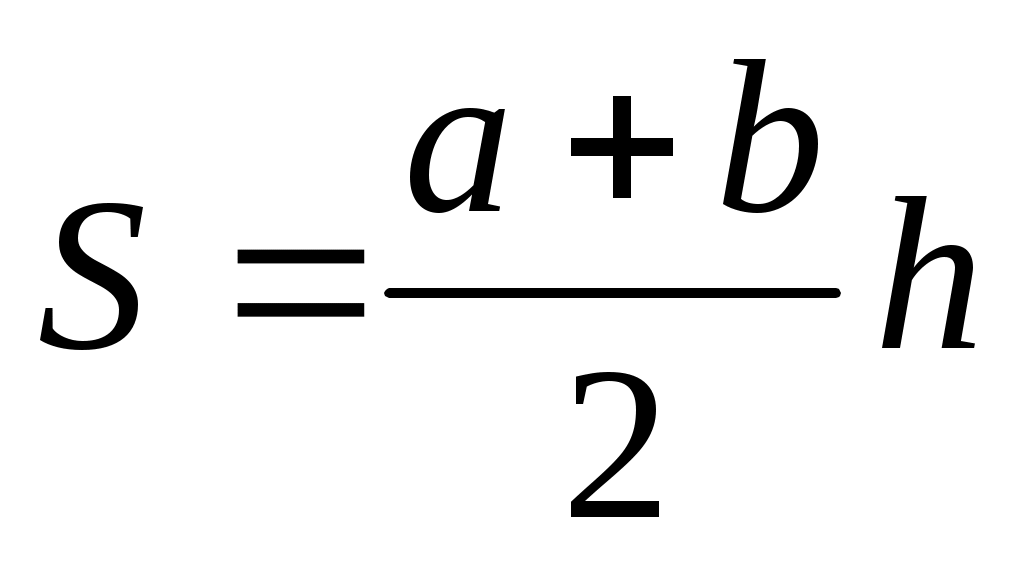 полусумма оснований на высоту полусумма оснований на высоту
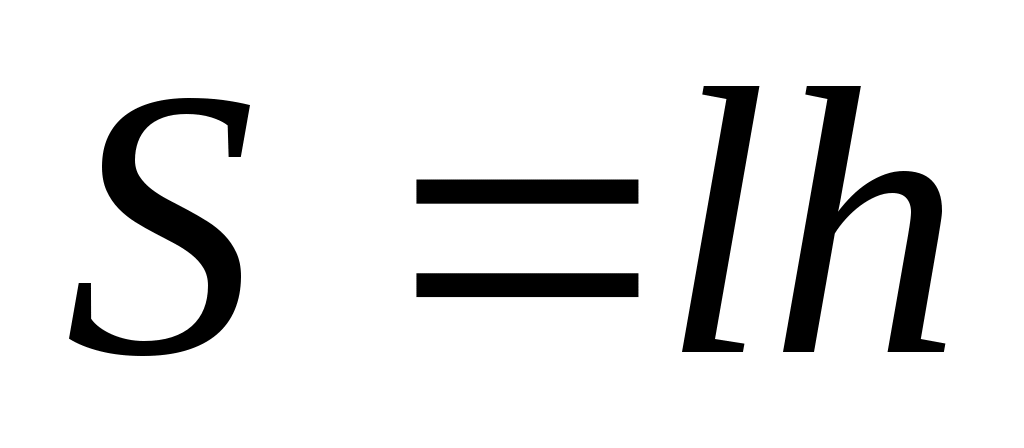 средняя линия на высоту средняя линия на высоту
7. 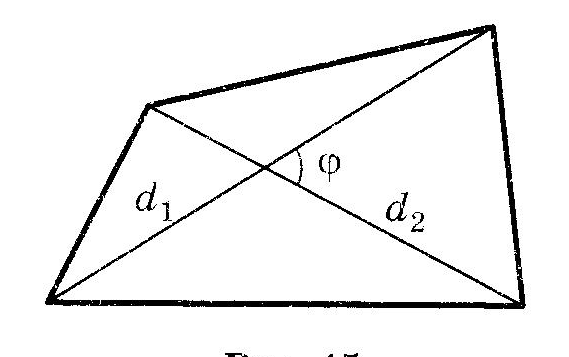 Площадь произвольного выпуклого четырехугольника. Площадь произвольного выпуклого четырехугольника.
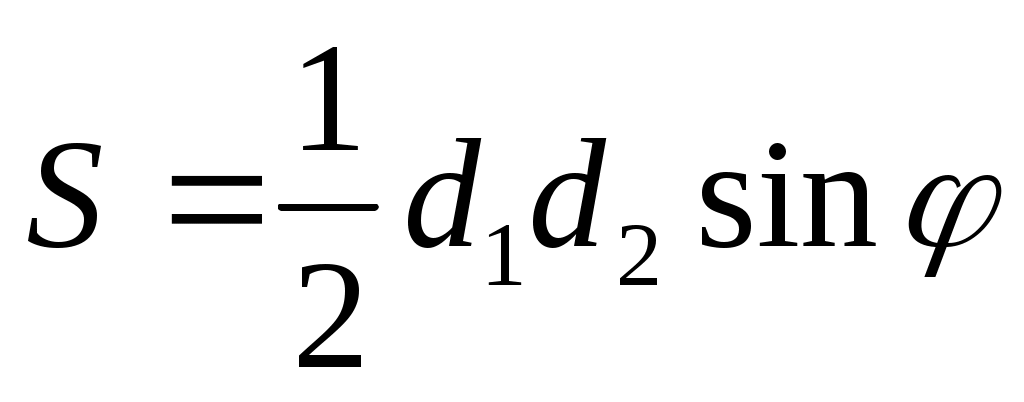 половина произведения двух диагоналей на синус угла между ними половина произведения двух диагоналей на синус угла между ними
8. 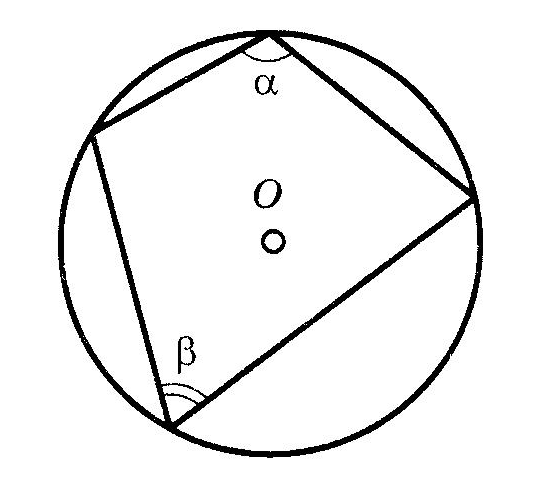 Площадь вписанного четырехугольника. Площадь вписанного четырехугольника.
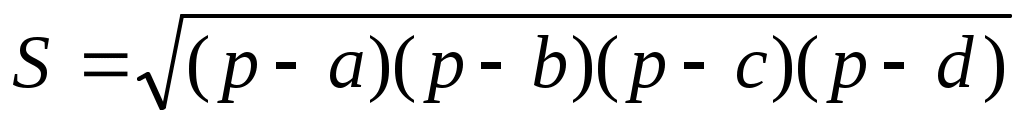 формула Брахмагупты формула Брахмагупты
Теоремы (о площадях треугольников)
Площадь прямоугольного треугольника равна половине произведения его катетов.
Если высоты двух треугольников равны, то их площади относятся, как основания.
Если угол одного треугольника равен углу другого треугольника, то их площади относятся как произведения сторон, заключающие равные углы.
|
 Скачать 2.24 Mb.
Скачать 2.24 Mb.