Интеграционное правопонимание. Основные понятия и факты геометрии 79 классов

• Название: Основные понятия и факты геометрии 79 классов
• Анкор: Интеграционное правопонимание
• Дата: 14.02.2023
• Размер: 2.24 Mb.
• Имя файла: -1822024027.doc
• Тип: Документы; #936370
• страница: 3 из 8

Прямоугольный треугольник

Опр. Треугольник называется прямоугольным, если у него есть прямой угол.

Опр. Сторона, лежащая против прямого угла в прямоугольном треугольнике, называется гипотенузой.

Опр. Стороны, заключающие прямой угол в прямоугольном треугольнике, называются катетами.

Равенство прямоугольных треугольников

Теорема (Признаки равенства прямоугольных треугольников), номера не важны, наличие или отсутствие слова “соответственно” важно: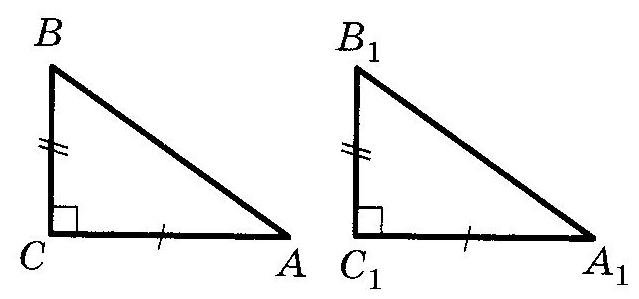

1. 
   (По двум катетам)
   

Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.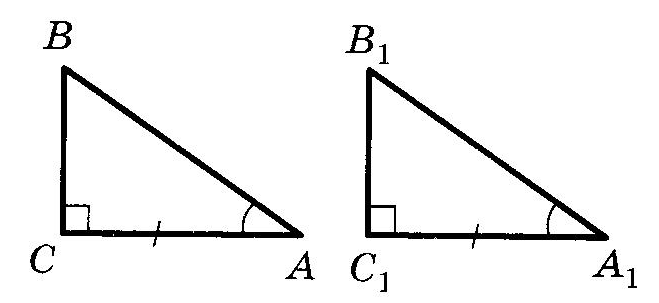

2. 
   (По катету и прилежащему острому углу)
   

Если катет и прилежащий острый угол одного прямоугольного треугольника равны катету и прилежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.

3. 
   (По катету и противолежащему острому углу)
   

Если катет и противолежащий острый угол одного прямоугольного треугольника равны катету и противолежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.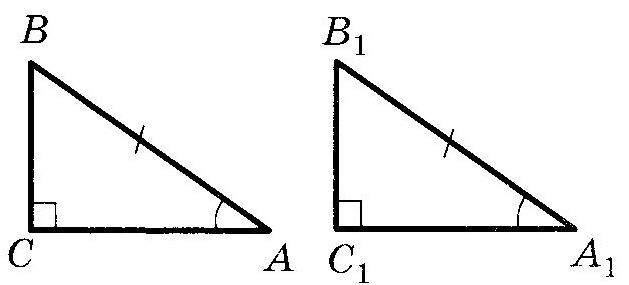

4. 
   (По гипотенузе и острому углу)
   

Если гипотенуза и острый угол одного прямоугольного треугольника равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.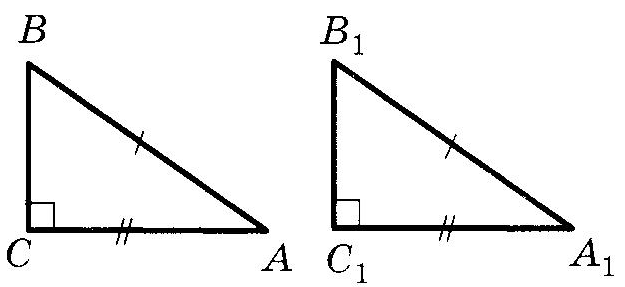

5. 
   (По катету и гипотенузе)
   

Если катет и гипотенуза угол одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.

II+III признаки можно объединить в один (По катету и острому углу)

Если катет и острый угол одного прямоугольного треугольника равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Четыре замечательные точки треугольника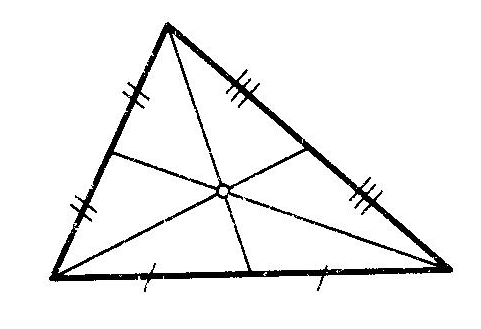

1. 
   точка пересечения медиан – центр тяжести треугольника.
   

Теорема о точке пересечения медиан треугольника

Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины.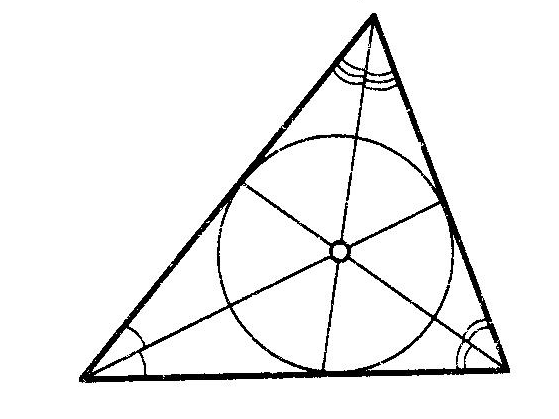

2. 
   точка пересечения биссектрис – центр вписанной окружности.
   
3. 
   точка пересечения высота (или их продолжений) – ортоцентр
   

4. 
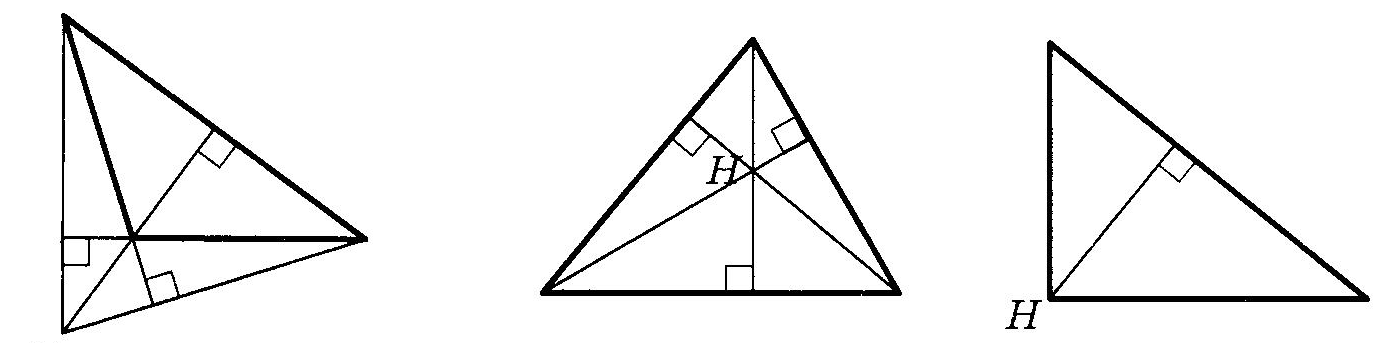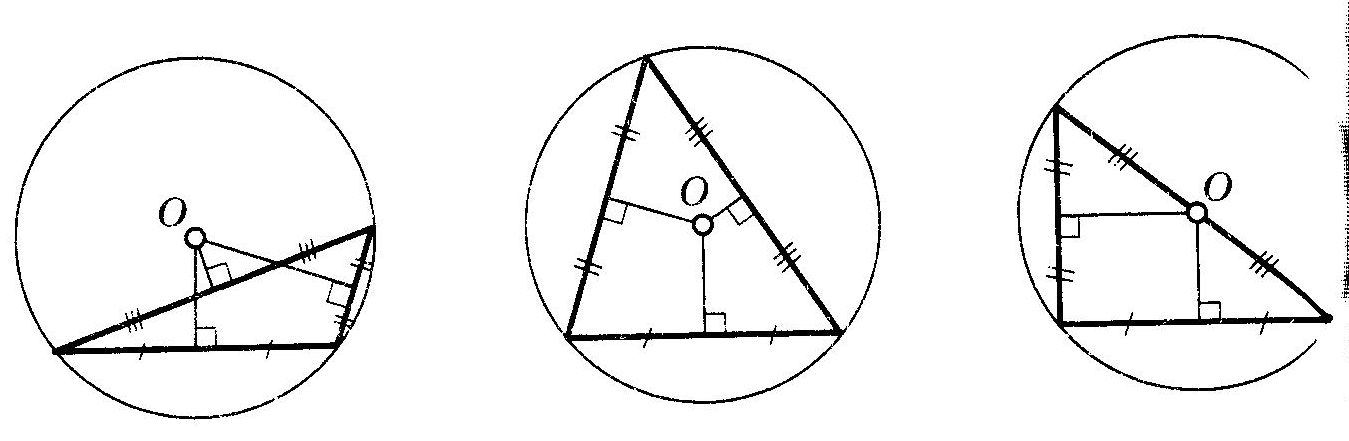   точка пересечения серединных перпендикуляров к сторонам – центр описанной окружности
   

Теоремы о треугольниках

Теорема (о сумме углов треугольника)

Сумма углов треугольника равна .
Следствие теоремы о сумме углов треугольника

1. 
   Сумма острых углов прямоугольного треугольника равна .
   
2. 
   В треугольнике не может быть более одного прямого или тупого угла.
   
3. 
   Сумма углов четырехугольника равна .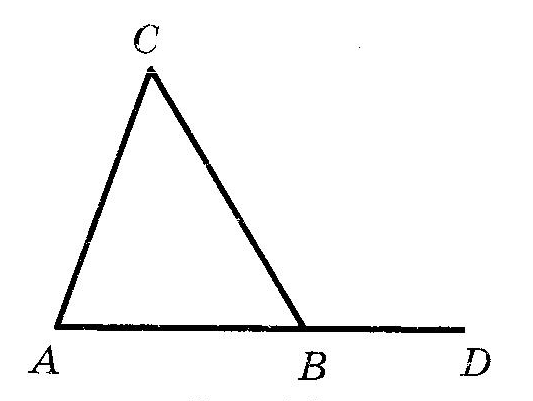
   

Опр. ВНЕШНИМ УГЛОМ треугольника называется угол, смежный с одним из углов треугольника.
Теорема (о внешнем угле треугольника)

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Следствия теоремы о внешнем угле треугольника

1. 
   Сумма внешних углов треугольника, взятых по одному у каждой вершины, равна .
   
2. 
   Внешний угол треугольника больше любого угла треугольника, не смежного с ним.
   

Теорема (свойство прямоугольного треугольника с углом )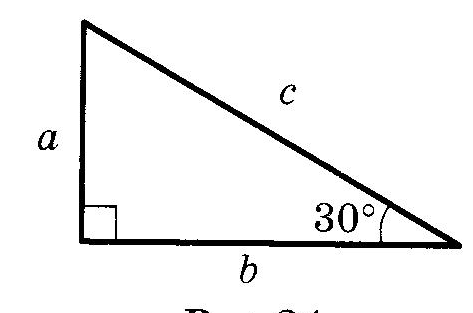

Катет прямоугольного треугольника против угла в равен половине гипотенузы.
Обратная теорема

Если катет прямоугольного треугольника равен половине гипотенузы, то угол против него равен .
Теорема (о медиане к гипотенузе)

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.

Обратная теорема.

Если медиана треугольника равна половине стороны, к которой она проведена, то этот треугольник прямоугольный.
Теорема (об угле между медианой и высотой к гипотенузе)

Угол между медианой и высотой прямоугольного треугольника, проведенными к гипотенузе, равен разности острых углов этого треугольника.
Теорема о биссектрисе треугольника

Биссектриса треугольника делит его сторону на отрезки, пропорциональные прилежащим сторонам.
Теорема

В остроугольном треугольнике отрезок, соединяющий основания двух высот, отсекает треугольник, подобный данному.
Опр. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Теорема (о средней линии треугольника)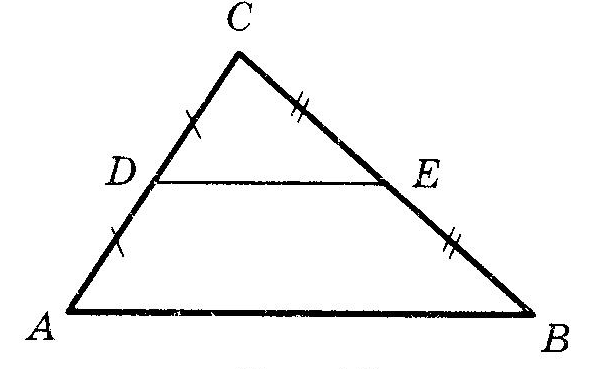

Средняя линия треугольника параллельная одной из сторон этого треугольника и равна ее половине.
Теоремы (об отрезках в прямоугольном треугольнике)

1. 
   Квадрат высоты прямоугольного треугольника, проведенной к гипотенузе, равен произведению проекций катетов на гипотенузу.
   
2. 
   В прямоугольном треугольнике квадрат катета равен произведению проекции этого катета и гипотенузы.
   

Теорема Пифагора

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.