Аудит информационной безопасности. АиБ_ЛБ1-5_Артюхова_БЭИС-20. Отчет по лабораторным работам 15 по дисциплине Аудит информационной безопасности

• Название: Отчет по лабораторным работам 15 по дисциплине Аудит информационной безопасности
• Анкор: Аудит информационной безопасности
• Дата: 29.11.2022
• Размер: 6.46 Mb.
• Имя файла: АиБ_ЛБ1-5_Артюхова_БЭИС-20.docx
• Тип: Отчет; #819087
• страница: 5 из 6

Лабораторная работа №4. Методы выбора мероприятий по повышению уровня информационной безопасности

Цель занятия: получить практические навыки применения математических методов для выбора мероприятий по повышению уровня информационной безопасности в организации.
2.1. Ниже представлена задача, которую надо решить двумя, описанными в теоретической части, методами:

– на основе пересечения нечетких множеств (значения весовых коэффициентов не учитывать);

– на основе методы выбора недоминируемых альтернатив с использованием нечеткого отношения предпочтения (значения весовых коэффициентов учитывать).

Задача 1. Выбрать наиболее подходящее решение для повышения уровня ИБ в организации на основе трех критериев: количество ролей пользователей информационной системы (чем больше, тем лучше), количество подключаемых проверок антивирусной системы (чем больше, тем лучше), стоимость приобретения и сопровождения (чем меньше, тем лучше). Cтепень значимости критериев принять: w1=0.5, w2=0.4, w3=0.1. При подсчете значений функции принадлежности использовать метод пропорций. Исходные данные приведены в таблице. В ответе указать номер выбранной альтернативы по каждому методу, матрицы D, M_nd и M_Q2.
Таблица 1 – Исходные данные

	Альтернатива 1	Альтернатива 2	Альтернатива 3
Количество ролей пользователей ИС (↑)	15	20	30
Количество подключаемых проверок антивирусной системы(↑)	10	10	5
Стоимость приобретения и сопровождения (↓),тыс. $	1	2	3

Решение. Найдем значения μ_i для (1). Для определенность расчетов и возможности проверки ответов применим не экспертные оценки, а «метод пропорций», в котором лучшей альтернативе присваивается значение μ_i=1, а остальные рассчитываются с помощью пропорции от этой единицы.

Для 1-го критерия (чем больше его значение, тем лучше) лучшая альтернатива №3, так как для нее критерий имеет значение 30. Примем 30 за «1», то есть μ₁(а₃) = 1 и найдем остальные функции принадлежности по правилу «пропорций». Обозначим x = μ₁(а₁). Для первой альтернативы составим пропорцию:

15 – х,

30 – «1»,

отсюда х= 0.5, то есть μ₁(а₁)= 0.5.

Аналогично для 2-й альтернативы x = μ₁(а₂): 20 – х, 30 – «1», откуда х=20/30= 0.7, то есть μ₁(а₂) =0.7.

Аналогично для второго критерия: принимаем лучшую альтернативу №1 μ₂(а₁)=1, тогда μ₂(а₂)=1, μ₂(а₃)=0.5.

Для 3-го критерия ситуация другая – он чем он меньше, тем лучше, поэтому лучшая альтернатива №1, она имеет значение критерия 1. Примем μ₃(а₁)=1. Тогда для 2-й альтернативы обозначим (1/x) = μ₃(а₂) и пропорцию запишем в виде:

1 – «1»;

2 – (1/х),

откуда 1/х=2, следовательно х=μ₃(а₂) 1/2=0.5. Аналогично найдем μ₃(а₃)= 0.3. В результате совокупность функций принадлежности (1) можно представить таблицей 2.
Таблица 2 – Функции принадлежности

	Альтернатива 1	Альтернатива 2	Альтернатива 3
Критерий 1(чем больше его значение, тем лучше)	0.5	0.7	1
Критерий 2 (чем больше его значение, тем лучше)	1	1	0.5
Критерий 3(чем меньше его значение, тем лучше)	1	0.5	0.3
Результат пересечения по столбцам (min)	0.5	0.5	0.3

В таблице 2 по столбцам находим минимум (операция пересечения нечетких множеств), это реализуется нахождение D по (2). Матрица-строка D записана в последней строке таблицы 2 жирным шрифтом. В нижней строке находим максимум (объединение нечетких множеств), он подчеркнут и находится в первом и втором столбцах, следовательно, лучшей будет считаться «Альтернатива 1» и «Альтернатива 2». Задача решена.

Рассмотрим второй способ выбора альтернатив – метод многокритериального выбора недоминируемых альтернатив на основе нечёткого отношения предпочтения.

Этапы этого метода до (1) включительно аналогичны предыдущему, поэтому будем считать, что значения функций принадлежности по всем критериям и альтернативам получены. Применим метод к предыдущему примеру. Возьмем данные из таблицы 2 и занесем их в таблицу 3.
Таблица 3 – Функции принадлежности

	Альтернатива 1	Альтернатива 2	Альтернатива 3
Критерий 1(чем больше его значение, тем лучше)	0.5	0.7	1
Критерий 2 (чем больше его значение, тем лучше)	1	1	0.5
Критерий 3(чем меньше его значение, тем лучше)	1	0.5	0.3

Занесем данные таблицы 3 в матрицу R: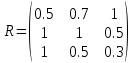

(3)

На основе R проводим попарное сравнение альтернатив по каждому критерию. Попарное сравнение легче проводить, чем когда сразу надо оценивать много вариантов. В данном случае дано три критерия → из R получим три матрицы используя выражение: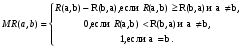

(4)

Здесь через a и b обозначены сравниваемые элементы R. Используя (4) рассчитываются элементы квадратных матриц MR1, MR2, MR3. Количество этих матриц будет равно количеству критериев, а в каждой из этих матриц количество строк (столбцов) будет равно количеству альтернатив.

Вначале сформируем матрицу MR1. Рассмотрим первую строку в (3) и применим (4). Сначала в этой строке обозначим a=0.5, b=0.7. Так как 0.5<0.7, то работает вторая строка (4) и получаем 0. Далее сдвигам b=1, получаем a=0.5< b=1, поэтому работает вторая строка (4) и получаем 0. После такого прохода получили одну строку новой матрицы MR1: (1 0 0).

Теперь продолжаем рассматривать первую строку из (3), но переходим ко второму столбцу: a=0.7. Назначаем b=0.5– первый элемент строки. Выполняем аналогичные расчеты по (4). В данном случае a=0.7>b=0.5, следовательно, применяем 1-ю строку (4) и получаем: 0.7–0.5=0.2. Сдвигаем b на третий элемент строки b=1. В данном случае снова a=0.7
Продолжаем рассматривать первую строку из (3), но переходим к третьему столбцу: a=1. Проводим аналогичные вышеизложенным расчеты. Но можно сразу увидеть, что этот элемент больше остальных в строке, поэтому третья строка матрицы MR1: (0.5 0.3 1). В итоге получаем матрицу: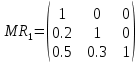

(5)
Далее формируем матрицу MR2 рассматривая вторую строку в (3) и применяя (4). Расчеты аналогичны, поэтому приведем сразу вид этой матрицы: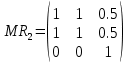


Аналогично формируем матрицу MR3 рассматривая третью строку в (3):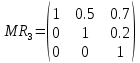


Полученные матрицы «накладываем» друг на друга и вертикально «пробиваем» выбирая в этой пробивке минимальный элемент. В результате получаем матрицу Q1.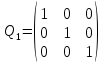

На основе матрицы Q1 проводится расчет матрицы-строки M_nd по формуле: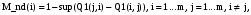
(6)

если Q1(j,i) < Q1(i, j,), то принимается Q1(j,i) – Q1(i, j,) = 0,
где sup – верхняя граница (максимальное значение), i,j – индексы элементов Q1.

Применим (6) к матрице Q1.

M_nd(1) = 1 – sup(Q1(2,1)– Q1(1,2); Q1(3,1)– Q1(1,3))=1–sup(0–0;0–0)=1.

M_nd(2) = 1 – sup(Q1(1,2)– Q1(2,1); Q1(3,2)– Q1(2,3))=1–sup(0–0;0–0)=1.

M_nd(3) = 1 – sup(Q1(1,3)– Q1(3,1); Q1(2,3)– Q1(3,2))=1–sup(0–0;0–0)=1.

В результате получаем матрицу-строку: M_nd = (1 1 1).

Зададим весовые коэффициенты, отражающие важность критериев с точки зрения ИБ: w1=0.5, w2=0.4, w3=0.1. Формируем матрицу:

Q2=w1MR1+w2 MR2+ w3MR3,

которая принимает вид: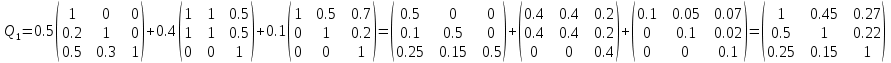


По Q2, аналогично как для Q1, по (6) рассчитываем матрицу-строку M_Q2:
M_Q2(1) = 1 – sup(Q2(2,1)–Q2(1,2); Q2(3,1)–Q2(1,3))=1–sup(0.5–0.45;0.25–0.27)= 1 – sup(0.05; 0)=1 – 0.05 = 0.95.

M_Q2(2) = 1 – sup(Q2(1,2)– Q2(2,1); Q2(3,2)– Q2(2,3))=1– sup(0.45–0.5; 0.15–0.22)= 1 – sup(0; 0) = 1 – 0= 1.

M_Q2(3) = 1 – sup(Q2(1,3)–Q2(3,1); Q2(2,3)–Q2(3,2))=1– sup(0.27–0.25; 0.22–0.15)= 1 – sup(0.02; 0.07)= 1 – 0.07= 0.93.

В результате получаем матрицу-строку: M_Q2= (0.95 1 0.93).

На заключительном этапе находим матрицу-строку M как пересечение матриц-строк M_nd и M_Q2 используя операцию взятия минимума соответствующих элементов: М =M_nd M_Q2= (1 1 1) (0.95 1 0.93) = (0.95 1 0.93).

В матрице М выбираем максимальный элемент – это 1, он является вторым элементом, следовательно, по данному методу выбираем вторую альтернативу.

2.2. Написать программу, автоматизирующую расчеты по методу пересечения нечетких множеств.

Входные данные программы: таблица условия задачи. Значения весовых коэффициентов можно не учитывать.

Выходные данные: номер альтернативы и матрица D.

Рекомендуемая среда реализации – MatLAB. Запустить программу с исходными данными задачи и сравнить результаты ее работы с результатами, полученными в п. 2.1.



Программа была написана на языке программирования C#. Листинг программы представлен ниже. Скриншоты работы программы представлены на рисунках 4.1 – 4.3.

Листинг программы:

Person[] students = { new Person("Tom"), new Person("Bob"), new Person("Sam") };

Person[] employees = { new Person("Tom"), new Person("Bob"), new Person("Mike") };

 

// объединение последовательностей

var people = students.Union(employees);

 

foreach (Person person in people)

    Console.WriteLine(person.Name);

 

 

class Person

{

    public string Name { get;}

    public Person(string name) => Name = name;

 

    public override bool Equals(object? obj)

    {

        if (obj is Person person) return Name == person.Name;

        return false;

    }

    public override int GetHashCode() => Name.GetHashCode();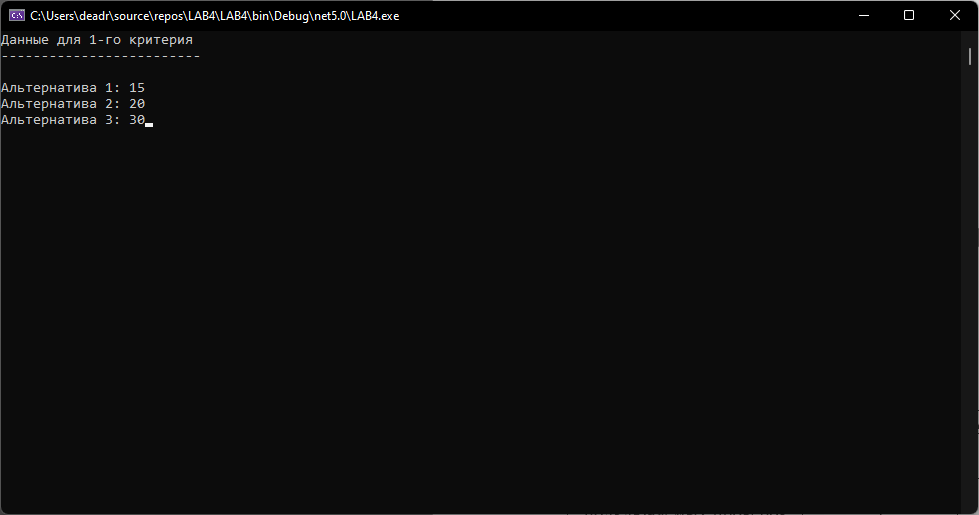

}


Рисунок 4.1 – Ввод данных для Критерия №1, Критерия №2 и Критерия №3


Рисунок 4.2 – Ввод параметра для Критерия №1, Критерия №2, Критерия №3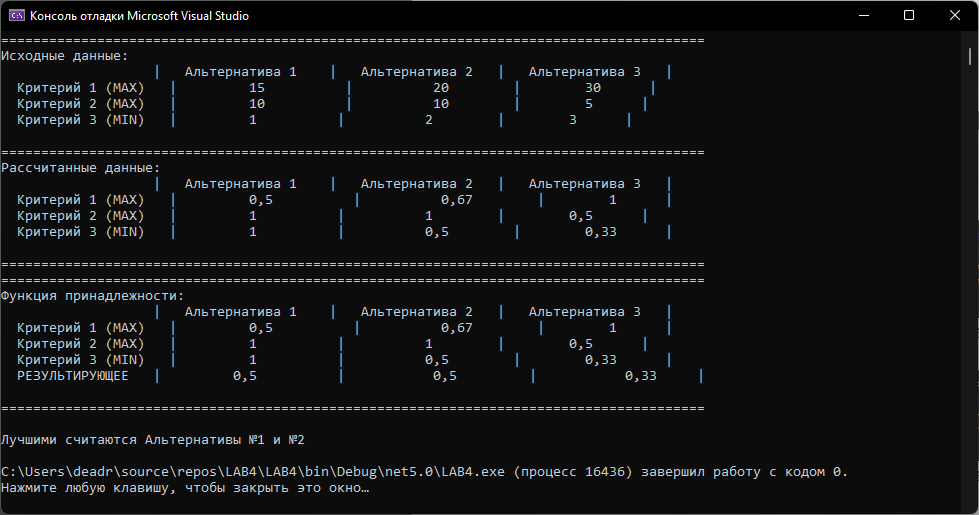


Рисунок 4.3 – Вывод программы
Вывод: в ходе выполнения лабораторной работы №4 были получены навыки применения математических методов для выбора мероприятий по повышению уровня информационной безопасности в организации.