Аудит информационной безопасности. АиБ_ЛБ1-5_Артюхова_БЭИС-20. Отчет по лабораторным работам 15 по дисциплине Аудит информационной безопасности

• Название: Отчет по лабораторным работам 15 по дисциплине Аудит информационной безопасности
• Анкор: Аудит информационной безопасности
• Дата: 29.11.2022
• Размер: 6.46 Mb.
• Имя файла: АиБ_ЛБ1-5_Артюхова_БЭИС-20.docx
• Тип: Отчет; #819087
• страница: 6 из 6

Лабораторная работа №5. Оценка состояния информационной безопасности на основе графа перехода состояний

Цель занятия: получить практические навыки оценки состояния информационной безопасности (ИБ) на основе графа перехода состояний.
1. Изучить теоретические положения. Вариант задания представлен ниже.

Вариант 1. Граф переходов состояний показан на рисунке. Интенсивности переходов (1/час): µ₁ = 0.1 λ₁ = 0.2 λ₂ = 0.6 λ₃ = 0.7.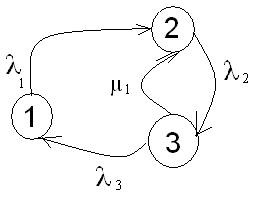


2. Записать для своего варианта СДУ Колмогорова, перейти от нее к системе линейных алгебраических уравнений (СЛАУ) и решить ее – найти P_i(∞).

Получаем уравнения:

P₁’(t) = λ₄P₃(t)-( λ₁+ λ₂)P₁(t), P₂’(t) = λ₁P₁(t)- λ₃P₂(t)+μ₁P₃(t),

P₃’(t) = λ₂P₁(t)+λ₃P₂(t)-(μ₁+λ₄)P₃(t), P₁(t)+P₂(t)+P₃(t)=1 – нормировочное уравнение, где P₁(t), P₂(t), P₃(t) – вероятности соответствующих состояний.

На практике интерес часто представляют установившиеся значения вероятностей, при t →∞, когда закончились все переходные процессы. В этом случае производные слева становятся равными нулю, и система дифференциальных уравнений превращается в систему из четырех линейных алгебраических уравнений, которые можно решать методом Гаусса.

Примем P₁(∞), P₂(∞), P₃(∞) за x₁, x₂ и x₃. А также все значения умножим на 100 для облегчения расчетов.

Получаем следующую СЛАУ: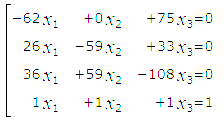



Матричный вид: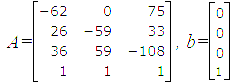



Для решения построили расширенную матрицу: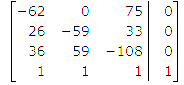



В ходе решения уравнений методом Гаусса получаем следующую СЛАУ: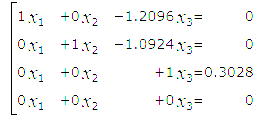



Следовательно, x1=1,2096*x3; x2=1,0924*x3; x3=0,3028.

Подставив нижние выражения в верхние, получим решение:

P₁(∞) = 0.2784, P₂(∞) = 0.3065, P₃(∞) = 0.3028.

Если считать состояния 2 и 3 как удовлетворяющие требованиям к уровню ИБ, а 1 как не удовлетворяющее, то коэффициент готовности системы будет равен: k_Г = P₂ (∞)+ P₃ (∞) = 0.3065+0.3028=0.6093.

3. Численно решить СДУ ее в любой программной среде (например, MatLAB) и построить графики изменения вероятностей состояния во времени P_i(t). Сравнить установившиеся значения вероятностей P_i(∞) с найденными в пункте 2 для СЛАУ. Если они не совпадают – найти причину.

Текст функции:

function [dP]=diffur1(t,P)

global L1 L2 L3 m1

dP=zeros(4,1);

dP(1,1)=-L1*P(1,1)+m1*P(4,1);

dP(2,1)=L1*P(1,1)-L2*P(2,1);

dP(3,1)=L2*P(2,1)-L3*P(3,1);

dP(4,1)=L3*P(3,1)-m1*P(4,1);

end

Текст программы:

clc, clear

global L1 L2 L3 m1 % определили интенсивности переходов как глобальные переменные

L1=20;L2=60;L3=70;m1=10; % определяем значения интенсивностей

tmax=0.25; % время расчета, выбирается исходя из условия, чтобы закончились переходные процессы %– графики вероятностей вышли на горизонтальный участок

P= [0.3;0.3;0.2;0.2]; % вектор начальных значений, числа произвольные, но их сумма =1

[T,Z] = ode45('diffur1', [0,tmax],P); % решение системы диф. ур.

plot(T,Z(:,1),'r',T,Z(:,2),'y',T,Z(:,3),'g',T,Z(:,4),'k') % графики вероятностей по результатам ode45

xlabel('время')
gtext('P0')

gtext('P1')

gtext('P2')

gtext('P3')

Z(end,1) % берем последнее значение 1-го столбца, это установившееся значение Р0

Z(end,2) % берем последнее значение 2-го столбца - установившееся значение Р1

Z(end,3) % берем последнее значение 2-го столбца - установившееся значение Р2

Z(end,4) % берем последнее значение 2-го столбца - установившееся значение Р3

disp('проверяем, сумма должна быть равна 1'),Z(end,1)+Z(end,2)+Z(end,3)+Z(end,4)

disp('Коэффициент готовности:'),Z(end,2)+Z(end,3)
clc, clear

global L1 L2 L3 m1

tmax=0.25;

P= [0.3;0.3;0.2;0.2]; % вектор начальных значений, числа произвольные, но их сумма =1

lamda1=[10,15,20,25,30];

mu1=[1,5,10,15,20];

[X,Y]=meshgrid(lamda1,mu1)

for m1=[1,5,10,15,20]

for L1=[10,15,20,25,30]

[T,Z] = ode45('diffur1', [0,tmax],P);

disp('m1'),m1

disp('L1'),L1

disp('Kг:'),Z(end,2)+Z(end,3)

end

end

Z=[0.0321 0.0308 0.0298 0.0294 0.0293;0.0930 0.1039 0.1102 0.1142 0.1171;0.1336 0.1566 0.1711 0.1811 0.1884;0.1566 0.1884 0.2097 0.2249 0.2364;0.1711 0.2097 0.2364 0.2559 0.2708]

surfc(X,Y,Z)

xlabel('lamda1'),ylabel('mu1'),zlabel('kг')

[Z1 I]=max(Z);[k_opt j]=max(Z1)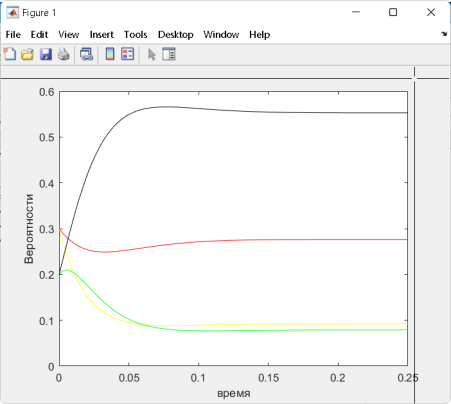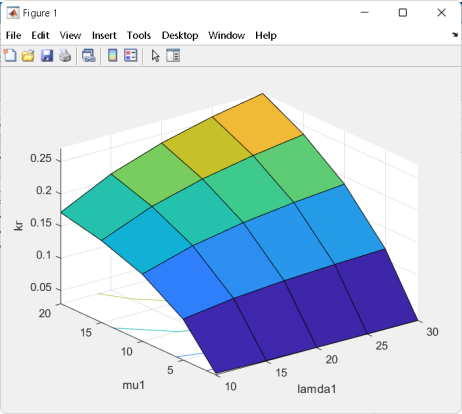


Рисунок 5.1 – График вероятностей и 3D-график в MatLAB
4. Вычислить коэффициент готовности k_г, считая допустимыми состояния под номерами 2 и 3.

Если считать состояния 2 и 3 как удовлетворяющие требованиям к уровню ИБ, а 1 как не удовлетворяющее, то коэффициент готовности системы будет равен: k_Г = P₂ (∞)+ P₃ (∞) = 0.3065+0.3028=0.6093.
Контрольные вопросы

1. Как могут быть реализованы угрозы безопасности ПДн?

Угрозы безопасности ПДн могут быть реализованы за счет утечки ПДн по техническим каналам (технические каналы утечки информации, обрабатываемой в технических средствах ИСПДн, технические каналы перехвата информации при ее передаче по каналам связи, технические каналы утечки акустической (речевой) информации) либо за счет несанкционированного доступа с использованием соответствующего программного обеспечения.

2. Что понимается под угрозами безопасности ПДн при их обработке в ИСПДн?

Под угрозами безопасности ПДн при их обработке в ИСПДн понимается совокупность условий и факторов, создающих опасность несанкционированного, в том числе случайного, доступа к персональным данным, результатом которого может стать уничтожение, изменение, блокирование, копирование, распространение персональных данных, а также иных несанкционированных действий при их обработке в информационной системе персональных данных.

3. Какая градация исходной степени защищенности используются в соответствии с «Методикой определения актуальных угроз безопасности персональных данных…»?

Для характеристики исходной степени защищенности используют следующие градации: высокая, средняя и низкая.

4. Какая градация принята для характеристики вероятности реализации угрозы ПДн?

• 
  маловероятно - отсутствуют объективные предпосылки для осуществления угрозы;
  
• 
  низкая вероятность – объективные предпосылки для реализации угрозы существуют, но принятые меры существенно затрудняют ее реализацию;
  
• 
  средняя вероятность – объективные предпосылки для реализации угрозы существуют, но принятые меры обеспечения безопасности ПДн недостаточны;
  
• 
  высокая вероятность – объективные предпосылки для реализации угрозы существуют и меры по обеспечению безопасности ПДн не приняты.
  

5. Сформулируйте правила составления СДУ Колмогорова.

1.Уравнений записывается столько, сколько состояний, плюс одно нормировочное (сумма вероятностей состояний равна единице).

2.Слева в каждом уравнении записывается производная от вероятности рассматриваемого состояния.

3.Справа от знака равно записывается сумма произведений вероятностей состояний, из которых стрелка выходит на интенсивность перехода по соответствующей стрелке. В каждом уравнении учитываются только те стрелки, которые входят или выходят из состояния, производная которого записана слева от знака равенства. Если стрелка входит в рассматриваемое состояние (стоящее слева от знака равенства), то произведение берется со знаком плюс. Если стрелка выходит из состояния, производная которого записанного слева в уравнении – то произведение берется со знаком минус.
Вывод: в ходе выполнения лабораторной работы №5 были получены навыки оценки состояния информационной безопасности (ИБ) на основе графа перехода состояний.