Подземная гидромеханика
 Скачать 3.56 Mb. Скачать 3.56 Mb.
|
|
7.1.6. Приток к бесконечным цепочкам и кольцевым батареям скважин При рациональной системе разработки нефтяных месторождений скважины располагают обычно в виде рядов, расставленных вдоль контура нефтегазоносности и контура питания. Эти линии называются батареями или рядами скважин. Без большой погрешности можно считать дебит скважин в каждом ряду одинаковым, если в каждом ряду скважины находятся в одинаковых условиях. Дебиты же скважин в разных рядах будут отличаться друг от друга. Наибольший дебит имеет первый ряд, ближайший к контуру питания, а по мере удаления дебит уменьшается. Поэтому число одновременно работающих рядов редко превышает два-три, и последующие ряды включаются по мере приближения контура нефтегазоносности. Когда вода подошла к первому ряду, то он выключается и включается один из следующих рядов и так далее. В этом случае число неизвестных уменьшается от числа скважин n до числа рядов N (обычно число рядов не превышает 2-4), что значительно упрощает решение задачи пункта 7.1.2. 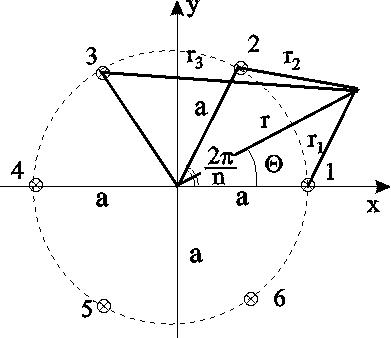 Рис. 7.8. Схема кольцевой батареи Приток к скважинам кольцевой батареи. Пусть центры скважин располагаются в вершинах правильного n-угольника, т.к. что скважины образуют кольцевую батарею радиуса а (рис. 7.8). Контур питания удалён от скважин на расстояние, значительно превышающее радиус батареи, и тогда можно считать, что все скважины равноудалены от контура питания на расстояние rк. Будем считать, что на контуре питания поддерживается постоянное значение потенциала к и на контуре скважин потенциал постоянен и равен с. В данной постановке, следовательно, надо решить задачу о плоском течении к n точечным стокам, размещённым равномерно на окружности радиуса а. Для получения формулы дебита скважин воспользуемся формулой (7.2): где G - массовый дебит любой скважины батареи, rj - расстояния от некоторой точки пласта до всех nскважин; h - толщина пласта. Граничные условия: на контуре питания =к=const,при rj=rк; на контуре скважины =с=const, при r1=rс; rj(j1)=2asin[(n-1)/n]. Используя данные граничные условия, преобразуем формулу (7.15): 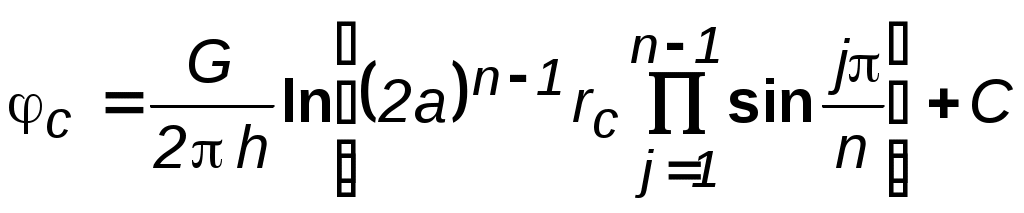 . (7.17) . (7.17)В последнем выражении Тогда (7.17) перепишется в виде и из (7.16), (7.19) получим выражение для определения дебита скважины 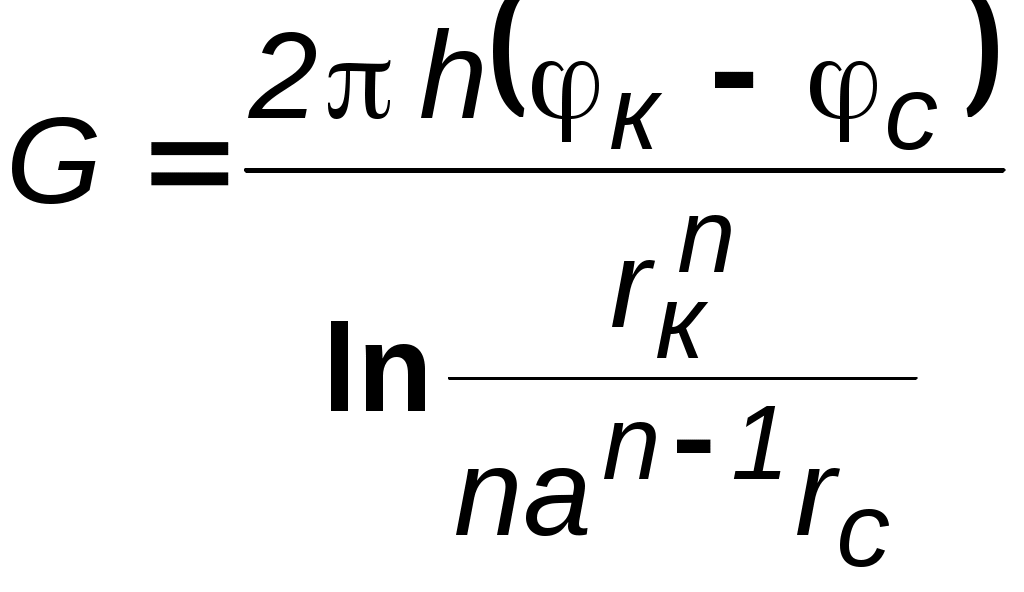 . (7.20) . (7.20)Формула (7.20) справедлива при любом целом n. В частности, при n=1 имеем выражение типа формулы Дюпюи для определения дебита при плоскорадиальном потоке: 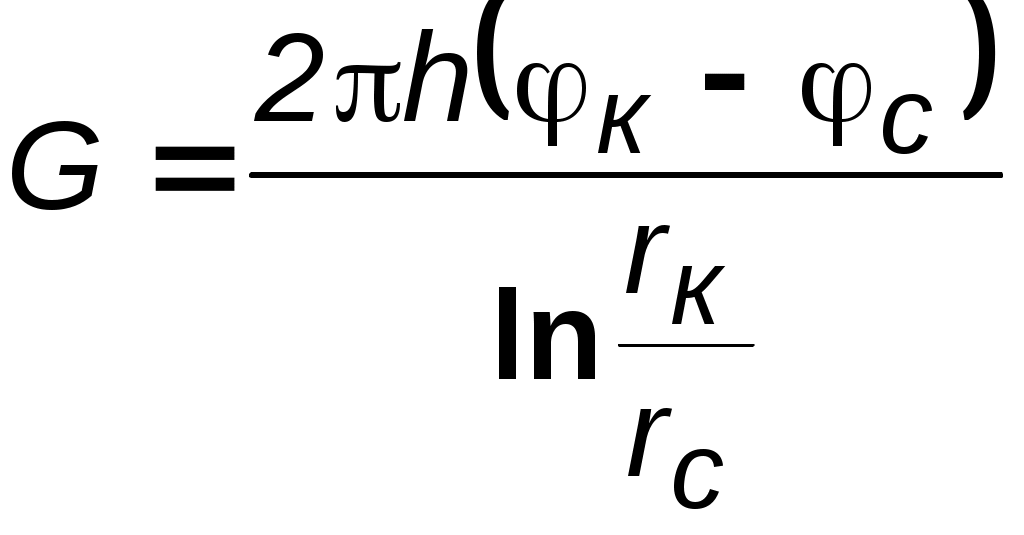 . (7.21) . (7.21)Формула (7.20) – приближенная. Её можно применять в случае, если размеры пласта во много раз больше площади внутри окружности батареи скважин, например, при водонапорном режиме, когда жидкость можно считать несжимаемой. Если же в пласте установился режим растворенного газа, то трудно ожидать, что площадь, занятая газированной жидкостью, простирается до границ пласта. Если расстояние до контура незначительно превышает радиус батареи, то, строго говоря, следует воспользоваться более точной формулой: 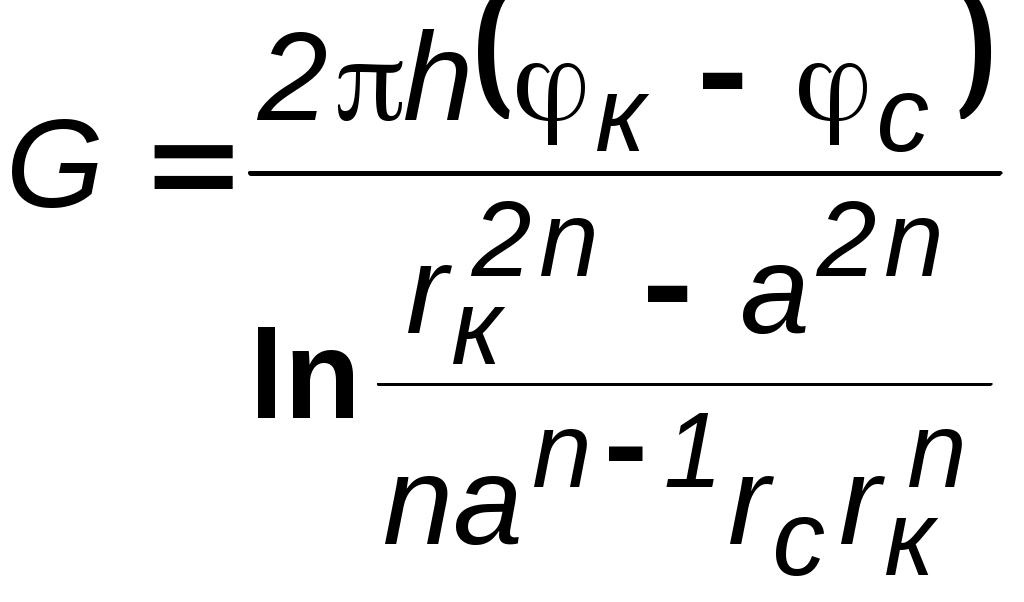 . (7.22) . (7.22)Эта формула при n=1 переходит в формулу определения дебита эксцентрично заложенной одиночной скважины (а - эксцентриситет скважины). В большинстве практических случаев можно пользоваться формулой (7.20), т.к. уже при rк=10а дебиты, подсчитанные по формулам (7.20) и (7.22), различаются не более чем на одну тысячную процента. Определим дебит батареи, умножив формулу (7.20) на число скважин в батарее n: 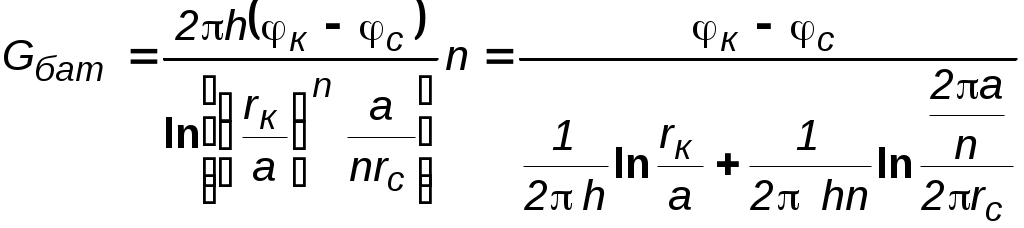 . (7.23) . (7.23)Рассмотрим поле течения в области действия круговой батареи, То есть построим семейства линий тока и изобар. Уравнение изобар получаем из (7.3) путём представления радиусов rj в полярной системе координат (рис. 7.8): Данное уравнение позволяет построить поле изобар, а линии тока пересекают изобары под прямым углом. 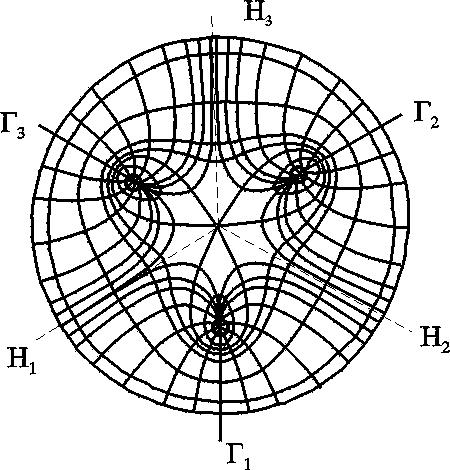 Рис. 7.9. Изобары и изолинии тока для кольцевой батареи из трёх скважин Плоскость течения (рис. 7.9) кольцевой батареи с n равнодебитными скважинами, размещенными в вершинах правильного многоугольника, делится на nравных частей (секторов) прямыми линиями тока Н, сходящимися в центре батареи и делящими расстояние между двумя соседними скважинами пополам. Эти линии тока называются нейтральными. Другое семейство прямых линий тока Гпроходит через центры скважин и делит сектор, ограниченный двумя нейтральными линиями, пополам. Это – главные линии. Семейство изобар подразделяется на два подсемейства, которые разграничиваются изобарой, пересекающей себя в центре батареи столько раз, сколько скважин составляет данную батарею. Первое подсемейство изобар определяет приток к отдельным скважинам и представляет собой замкнутые, каплеобразные кривые, описанные вокруг каждой скважины. Второе семейство – определяет приток к батарее в целом и представляет собой замкнутые кривые, описанные вокруг батареи. Скорость фильтрации по главным линиям максимальна, а по нейтральным линиям – минимальна. В центре кольцевой батареи скорость фильтрации равна нулю, т.е. частица жидкости, находящаяся в точке, в которой изобара пересекает сама себя, неподвижна. Такие точки фильтрационного поля называются точками равновесия и при разработке в окрестностях таких точек образуются “застойные области”. В условиях водонапорного режима в этих областях могут возникать “целики нефти”. Зная положения точек равновесия в пласте, можно находить рациональные приёмы для своевременной ликвидации целиков нефти. Одним из таких приёмов является изменение режима работы скважин, заставляющее нефть целика прийти в движение в нужном направлении. Для кольцевой батареи, на основе анализа формул (7.20)-(7.23), можно сделать ряд оценок эффекта взаимодействия: дебит изменяется непропорционально числу скважин и радиусу батареи (расстоянию между скважинами); с увеличением числа скважин дебит каждой скважины уменьшается при постоянном забойном давлении, т.е. растет эффект взаимодействия; взаимодействие скважин может практически не проявляться только при очень больших расстояниях между скважинами (в случае несжимаемой жидкости, строго говоря, влияние скважин распространяется на весь пласт); с увеличением числа скважин темп роста суммарного дебита батареи замедляется (рис. 7.1), а именно, сверх определённого предела увеличение числа скважин оказывается неэффективным в виду прекращения прироста дебита. Приток к прямолинейной батарее скважин. Рассмотрим, как и в предыдущем случае, приток к батарее при удалённом контуре питания в режиме поддержания постоянного забойного давления. В отличие от круговой батареи необходимо различать два случая: число скважин батареи нечетное; число скважин четное. В обоих случаях дебиты скважин, равноудаленные от середины или от концов батареи, будут одинаковы, а при разной удаленности будут отличаться. Последнее вызывается неодинаковой интенсивностью влияния со стороны скважин батареи на те или иные скважины. При этом при нечетном числе скважин дебит средней скважины отличается от дебитов других скважин. Дебиты равномерно расположенных скважин можно определить общим методом с использованием формулы (7.2). Можно вывести аналогичные уравнения для любой скважины прямолинейной батареи конечной длины в пласте с прямолинейным контуром питания, но с использованием дополнительно метода отображения. В этом случае запись уравнений оказывается громоздкой из-за необходимости учета не только взаимных расстояний между скважинами, но также расстояний между скважинами и воображаемыми источниками и расстояний между этими последними. Для практических расчетов можно использовать приближенную формулу П.П. Голосова для общего дебита скважин прямолинейной батареи: для нечетного числа скважин 2n+1, где n - любое целое число 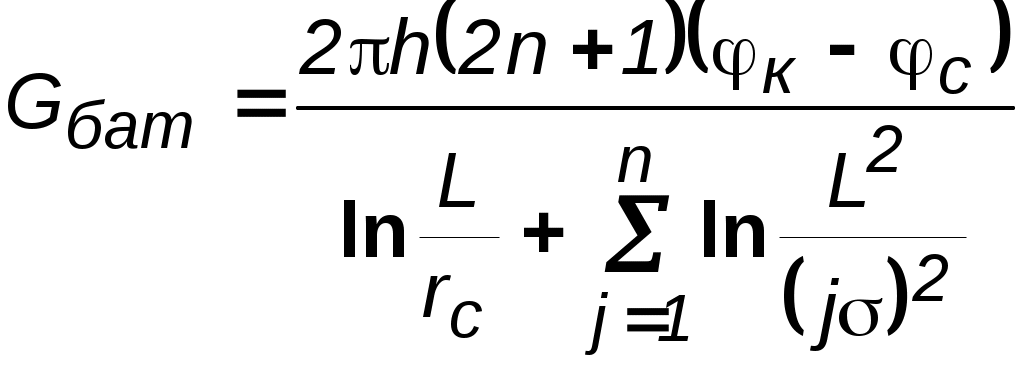 для четного числа скважин 2n 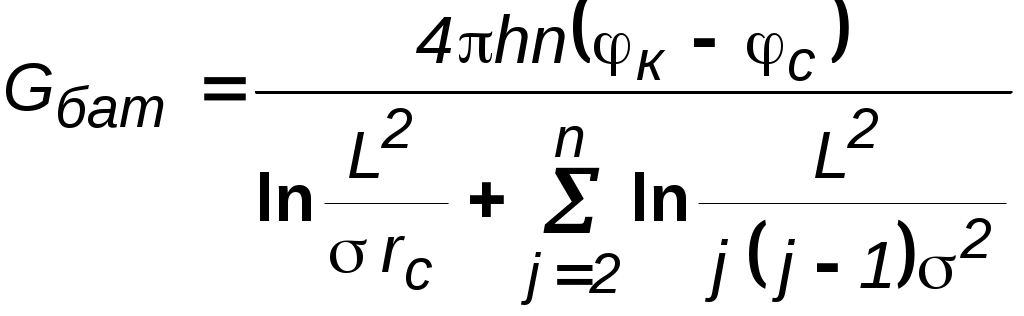 Здесь h– толщина пласта; – расстояние между скважинами; L – расстояние до контура. Ошибка в определении дебитов по данным формулам не превышает 3–4% при L=10км, rс=10см, при расстояниях между скважинами 100м 500м.. Приведенные формулы можно использовать при любом контуре питания, т.к. проведенные ранее исследования взаимодействия двух скважин показали, что форма контура питания пласта мало влияет на взаимодействие скважин. При этом, по мере приближения скважин к контуру питания эффект взаимодействия уменьшается, но в реальных условиях значительного удаления скважин от контура питания погрешность определения расстояния до контура даже в 100% не отражается значительно на эффекте взаимодействия. Для однородных пластов и жидкостей относительные изменения дебитов скважин, вызванные эффектом взаимодействия, не зависят от физико-геологических характеристик пласта и от физических параметров жидкости. 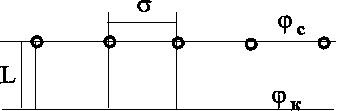 Рис. 7.10. Схема прямолинейной батареи скважин Рассмотрим фильтрационное поле (рис.7.10), поддерживаемое бесконечной цепочкой равностоящих скважин (требование бесконечности приводит к ликвидации граничных эффектов на концах батареи и равнодебитности скважин, так как все скважины оказываются в равных условиях притока к ним флюидов). Для получения формул дебита скважины бесконечной прямолинейной батареи воспользуемся формулой (7.20) дебита скважины кольцевой батареи. Положим, что rк = L + a; a = n /(2 ), (7.27) где L = const – разность между радиусом контура питания и радиусом кольцевой батареи а; = const – длина дуги окружности радиусом а между двумя соседними скважинами кольцевой батареи. Подставив значения rк, aв формулу (7.20), получим 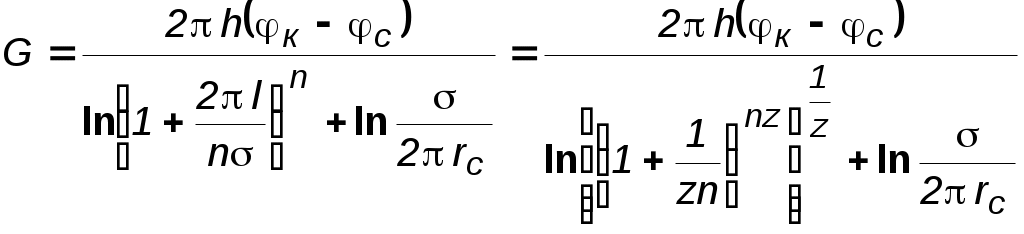 , (7.28) , (7.28)где z= / (2l). Переходя в данной формуле к пределу при n и учитывая, что 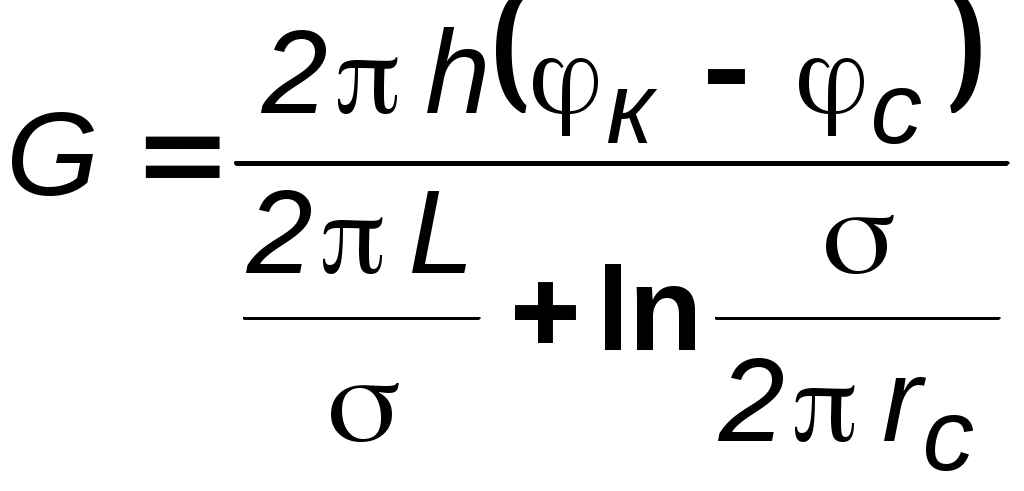 . (7.29) . (7.29)Здесь L – расстояние от контура питания до батареи; –- расстояние между скважинами батареи; h – толщина пласта. Суммарный дебит из n - скважин определится следующим выражением: 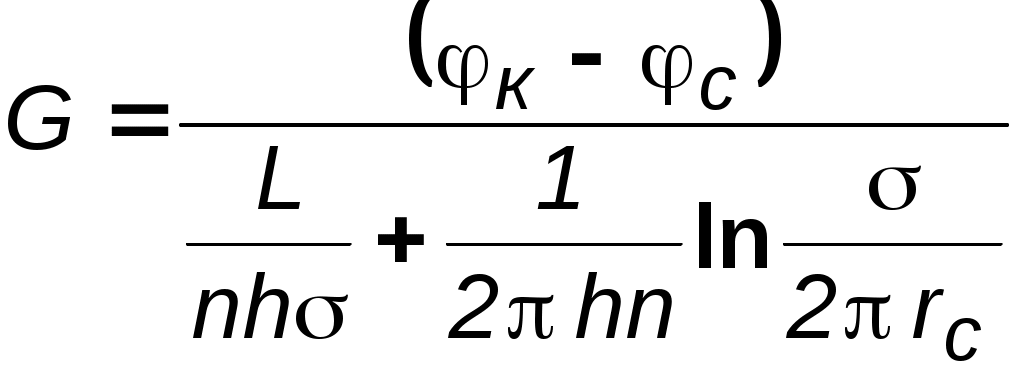 . (7.30) . (7.30)Для несжимаемой жидкости соотношение (7.35) можно переписать через давление и объёмный дебит 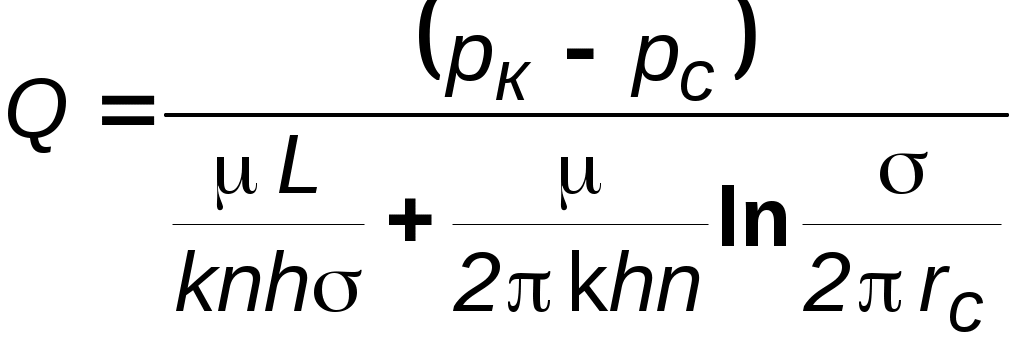 . (7.31) . (7.31)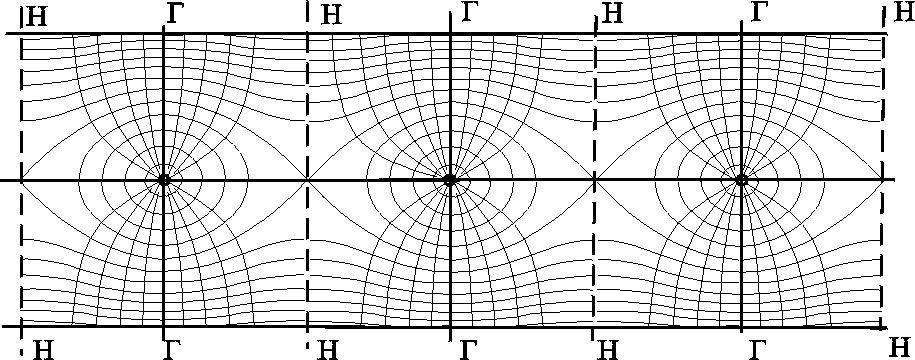 Рис.7.17. Фильтрационное поле для бесконечной батареи. Ортогональная сетка, изображающая фильтрационное поле бесконечной прямолинейной батареи, изображена на рис. 7.11 . Здесь, как и в кольцевой батарее, имеются главные и нейтральные линии тока перпендикулярные цепочке. Нейтральными линиями тока вся плоскость течения делится на бесконечное число полос, каждая из которых является полосой влияния одной из скважин, находящейся в середине расстояния между двумя соседними нейтральными линиями. Главные линии тока проходят через центры скважин параллельно нейтральным линиям. Изобара, бесчисленное множество раз пересекающая сама себя, отделяет изобары внешнего течения ко всей батареи, охватывающих всю цепочку скважин, от изобар притока к скважине, охватывающих только данную скважину. Точки пересечения граничной изобары являются точками равновесия и они делят интервал между двумя соседними скважинами пополам. 7.2. Метод эквивалентных фильтрационных сопротивлений (метод Борисова) Данный метод называется методом Борисова и позволяет сложный фильтрационный поток в пласте при совместной работе нескольких батарей эксплуатационных и нагнетательных скважин разложить на простейшие потоки – к одиночно работающей скважине и к одиночно работающей батареи. Реализация данного метода достигается введением понятий внутреннего и внешнего фильтрационных сопротивлений, которые придают простейший физический смысл членам уравнений, используемых для подсчетов дебитов и значений потенциальных функций. Для выяснения этих понятий сравним формулы (7.30) или (7.31) с законом Ома I=U / R, где I – ток, U– разность потенциалов и R – сопротивление. Из сравнения видно, что фильтрационное сопротивление определяется величиной знаменателя правой части (7.30), который состоит из двух слагаемых. Если в (7.30) оставить только первое слагаемое, то оно будет выражать дебит в прямолинейно-параллельном потоке через площадь величиной nh на длине L. Таким образом, первое слагаемое выражает фильтрационное сопротивление потоку от контура питания к участку прямолинейной бесконечной цепочки, занятому n скважинами, в предположении замены батареи галереей. Борисов назвал эту часть фильтрационного сопротивления – внешним фильтрационным сопротивлением: Оставим теперь в (7.30) только второе слагаемое. В этом случае получим аналог формулы Дюпюи для суммарного дебита n скважин при плоскорадиальном течении и в предположении, что каждая скважина окружена контуром питания длиной . Таким образом, второе слагаемое выражает местное фильтрационное сопротивление, возникающее при подходе жидкости к скважинам. Появление этого сопротивления объясняется искривлением линий тока у скважин и, по Борисову, оно получило название внутреннего На внешнее и внутреннее фильтрационные сопротивления разделяется также полное фильтрационное сопротивление кольцевой батареи: 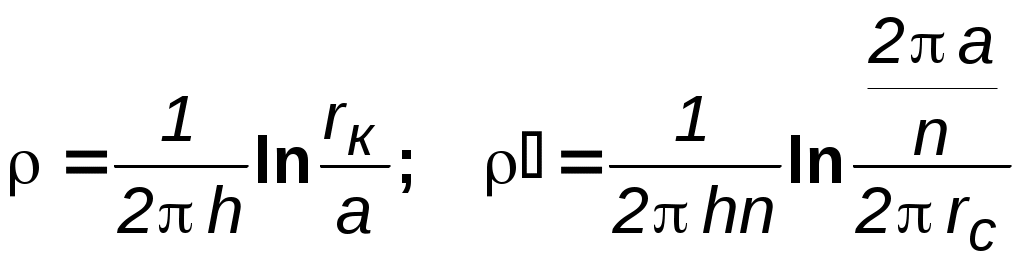 Здесь выражает фильтрационное сопротивление потоку от контура питания к кольцевой батареи радиуса а в предположении, что поток плоскорадиален и батарея заменена галереей. Внутреннее сопротивление / – это сопротивление плоскорадиального потока от воображаемого контура окружности длиной 2а/nк скважине. Величина 2а/n – длина дуги сектора радиуса а, который содержит одну из скважин батареи. 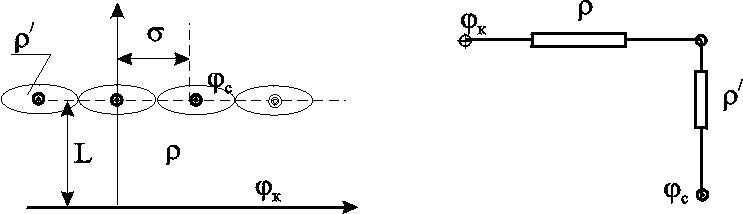 Рис. 7.12. Схема одной Рис. 7.13 Электрическая батареи схема одной батареи Электрическая схема в случае одной батареи (рис.7.12) имеет вид (рис.7.13). На рис.7.12 затемнены области внутреннего сопротивления. 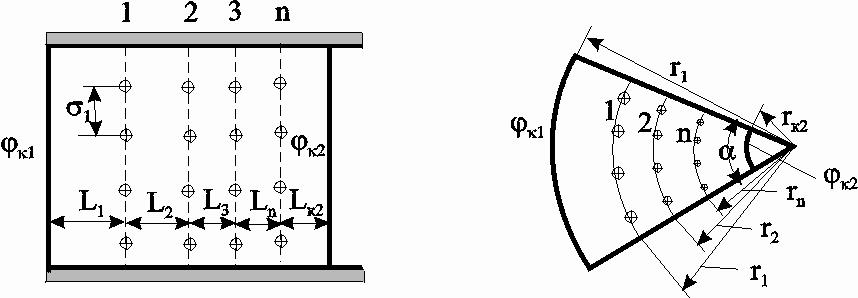 а b Рис.7.14. Схема n-батарей с двумя контурами питания: а) линейные батареи; b) кольцевые батареи Рассмотрим случай притока к n эксплуатационным и нагнетательным батареям скважин и составим схему сопротивлений. Предположим, что скважины i- й батареи имеют забойные потенциалы сi (i = 1,...,n), пласт имеет контурные потенциалы к1и к2 (рис. 7.14). Пусть к1 > к2. Очевидно, поток от контура питания к первому ряду скважин будет частично перехватываться первой батареей и частично двигаться ко второй. Поток ко второй батарее будет частично перехватываться второй батареей, частично двигаться к третьей и т.д. Этому движению отвечает разветвленная схема фильтрационных сопротивлений (рис. 7.15). 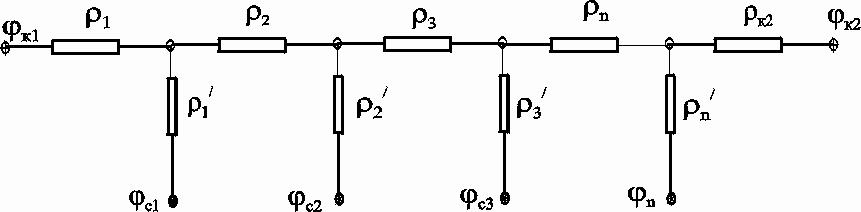 Рис. 7.15. Электрическая схема n-батарей с двумя контурами питания Расчет ведется от контура с большим потенциалом к контуру с меньшим потенциалом, а сопротивления рассчитываются по зависимостям: прямолинейная батарея круговая батарея где Li – расстояние между батареями (для i = 1 - L1 = Lк1 ); ri – радиусы батарей (для i = 1 - r0 = rк ); ki– число скважин в батарее. Дальнейший расчет ведется, как для электрических разветвленных цепей, согласно законам Ома и Кирхгоффа: Следует помнить, что для последовательных сопротивлений =i, а для параллельных - 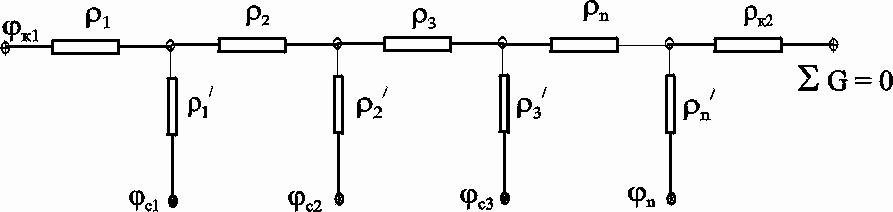 Рис.7.16. Электрическая схема n-батарей с двумя контурами питания (проницаемым и непроницаемым) Если одна из границ непроницаема, то расход через неё равен нулю, и в соответствующем узле схемы фильтрационных сопротивлений задаётся не потенциал, а расход. На рис. 7.16 показана схема в случае непроницаемости второго контура, где вместо потенциала к2 (рис.7.15) задано условие Gi = 0. Приведенные формулы тем точнее, чем больше расстояние между батареями по сравнению с половиной расстояния между скважинами. Если расстояние между скважинами много больше расстояния между батареями, то расчет надо вести по общим формулам интерференции скважин, или использовать другие виды схематизации течения, например, заменить две близко расположенные соседние батареи скважин с редкими расстояниями между скважинами (рис. 7.17,а) эквивалентной батареей – с суммарным числом скважин и расположенной посредине (рис.7.17,b). 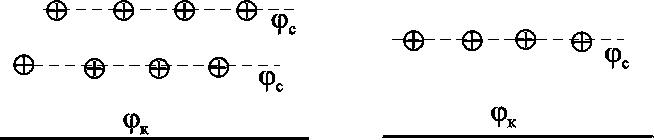 a b Рис. 7.17. Схема замены соседних батарей скважин одной батареей 7.3. Интерференция несовершенных скважин. В случае интерференции скважин несовершенных по степени вскрытия в условиях течения по закону Дарси вначале определяется дебит совершенных скважин с радиусами rс по формулам теории интерференции для притока к стокам и источникам на плоскости, а затем фильтрационное сопротивление каждой скважины увеличивается на величину коэффициентов несовершенства Сi (i = 1,...,4). При использовании метода эквивалентных фильтрационных сопротивлений двухчленный закон фильтрации надо представить в виде где Например, в схеме фильтрационных сопротивлений для условий линейного закона фильтрации, внутренние сопротивления следует заменить суммой 7.3.1. Взаимодействие скважин в анизотропном пласте 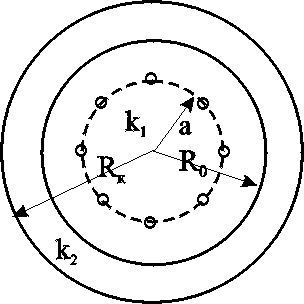 Рис. 7.18. Кольцевая батарея скважин при двухзональной неоднородности пласта При разработке часто возникают условия, при которых проницаемость в законтурной области меньше проницаемости внутри контура (рис.7.18). Пусть в круге радиуса R0 проницаемость k1, а в кольце Rкпроницаемость k2. При этом Rк >> a радиуса батареи. Поток к n эксплуатационным скважинам идёт от окружности радиуса R0 и дебит G1 каждой скважины определяется по (7.20), где вместо к следует поставить 0 – потенциал на границе двух сред, а вместо rк – R0. Во второй области поток плоскорадиален от контура Rк до укрупненной скважины радиуса R0 и дебит скважины Имея в виду, что в пределах каждой зоны k = const, распишем потенциал в виде = kФ+С, где 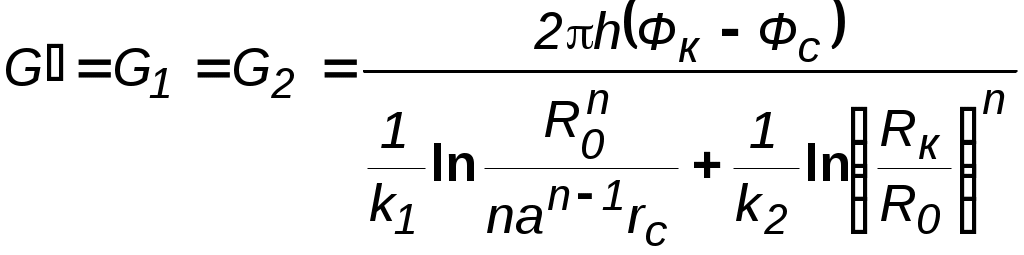 . (7.51) . (7.51)Для однородной несжимаемой жидкости Ф = р/, а вместо массового дебита G/ надо подставить объёмный дебит Q. Пользуясь (7.51), можно сравнить дебиты батареи при различных относительных размерах частей I и II пласта и при различных соотношениях между проницаемостями. Расчеты показывают, что при k1/k2 = < 1 величина коэффициента суммарного взаимодействия Рассмотрим случай, когда кольцевая батарея занимает область II, то есть область, примыкающую к контуру питания (а > R0). В этом случае 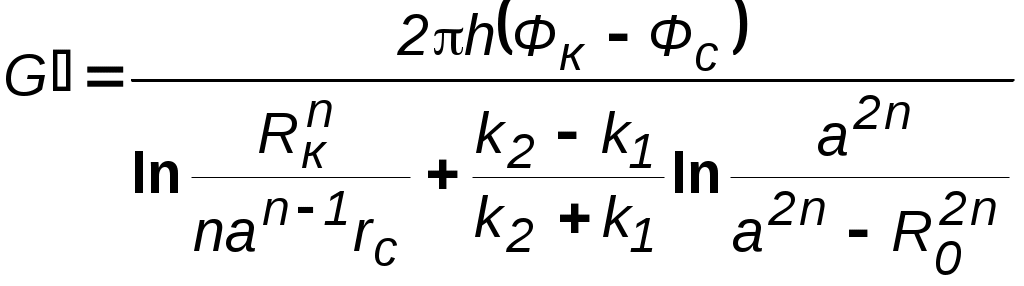 . (7.52) . (7.52)Для анизотропных пластов эффект взаимодействия будет значительно усиленным или ослабленным лишь при резком различии проницаемостей в двух определённых направлениях: в направлении линии расстановки скважин и в направлении, перпендикулярном к этой линии. Ослабление взаимодействия наблюдается в случае более низкой проницаемости в направлении линии расстановки скважин по сравнению с проницаемостью в перпендикулярном направлении. Усиление эффекта взаимодействия происходит в обратном случае. Таким образом, для уменьшения эффекта взаимодействия при закладывании новых скважин следует выбирать направление, в котором пласт наименее проницаем. Взаимодействие скважин. С целью выявления влияния радиуса скважин на дебит при взаимодействии скважин сравним дебиты скважин кольцевой батареи из n эксплуатационных скважин в двух случаях: 1)скважины имеют радиус rc и 2)скважины имеют радиус хrc. Из (7.20) следует 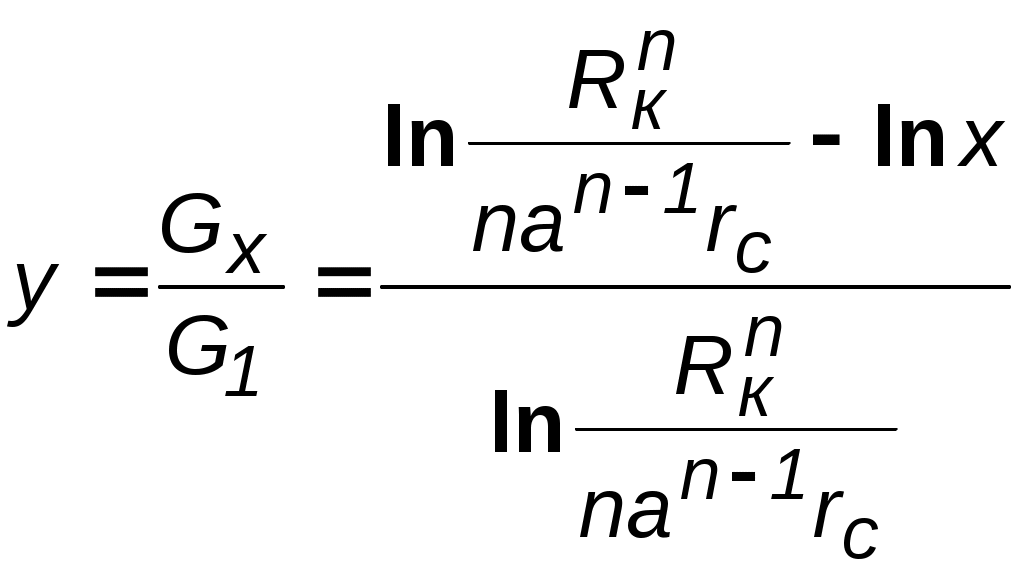 . (7.53) . (7.53)Кроме того, рассмотрим случай, если в центре батарей действует нагнетательная скважина с дебитом, равным дебиту батареи: 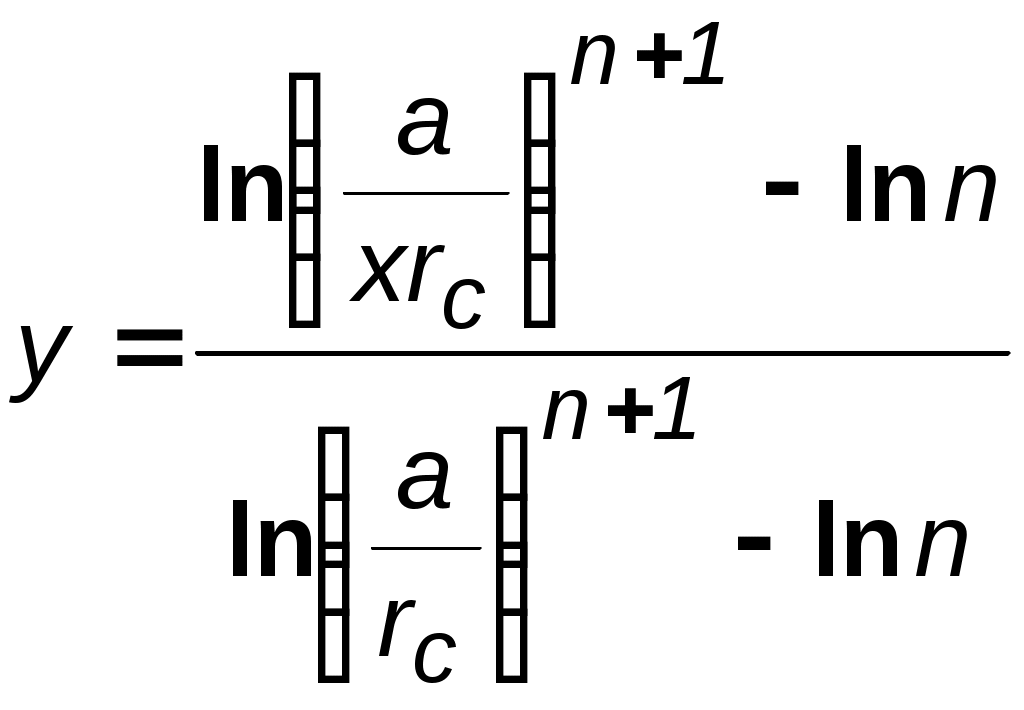 . (7.54) . (7.54)Из данных зависимостей следует, что с увеличением числа эксплуатационных скважин кольцевой батареи влияние их радиуса на дебит уменьшается, если отсутствует нагнетание жидкости в пласт. Если в центре батареи находится нагнетательная скважина, то влияние радиуса скважины на дебит будет больше, чем при отсутствии центрального нагнетания жидкости в пласт. При этом радиус скважины влияет на производительность больше, чем при одиночной эксплуатационной скважине. Число скважин при этом несущественно. Таким образом, взаимодействие эксплуатационных скважин с нагнетательными повышает влияние радиуса скважин на дебит. |
