Подземная гидромеханика

• Название: Подземная гидромеханика
• Дата: 30.11.2022
• Размер: 3.56 Mb.
• Имя файла: Posobie_PGM.doc
• Тип: Учебное пособие; #820975
• страница: 13 из 17

7. УСТАНОВИВШАЯСЯ ПОТЕНЦИАЛЬНАЯ ПЛОСКАЯ (ДВУХМЕРНАЯ) ФИЛЬТРАЦИЯ
Основная проблема разработки нефте-водо-газоносных пластов – расчет притока к одной или группе совершенных скважин. Точные решения, как правило, оказываются весьма сложными и громоздкими. При разработке проектов в настоящее время используют численные методы, связанные с довольно большими затратами как финансовыми, так и временными. Для оценочных целей и получения выражений для определения дебитов можно применять более простые приближенные, но вместе с тем достаточно точные методы расчета. Это методы, использующие аппарат функции комплексного переменного и свойства уравнения Лапласа.

При разработке нефтяных и газовых месторождений (НГМ) возникает два вида задач:

1. Задаётся дебит скважин и требуется определить необходимое для этого дебита забойное давление и, кроме того, давление в любой точке пласта. В данном случае величина дебита определяется значением предельной для имеющихся коллекторов депрессией, при которой ещё не наступает их разрушение, или прочностными характеристиками скважинного оборудования, или физическим смыслом. Это означает, например, невозможность установления нулевого или отрицательного забойного давления.





Рис. 7.1. Зависимость суммарного дебита от числа скважин
2. Задаётся забойное давление и требуется определить дебит. Последний вид условия встречается наиболее часто в практике разработки НГМ. Величина забойного давления определяется условиями эксплуатации. Например, давление должно быть больше давления насыщения для предотвращения дегазации нефти в пласте или выпадения конденсата при разработке газоконденсатных месторождений, что снижает продуктивные свойства скважин. Наконец, если возможен вынос песка из пласта на забой скважины, то скорость фильтрации на стенке скважины должна быть меньше некоторой предельной величины.

Следует отметить, что при эксплуатации группы скважин в одинаковых условиях, т.е. с одинаковым забойным давлением, дебит всего месторождения растёт медленнее увеличения числа новых скважин с теми же забойными условиями (рис.7.1). Увеличение дебита при этом требует понижения забойного давления.

Для решения поставленных задач необходимо решить задачу плоской интерференции (наложения) скважин.

Предположим, что пласт – неограниченный, горизонтальный, имеет постоянную мощность и непроницаемые подошву и кровлю. Пласт вскрыт множеством совершенных скважин и заполнен однородной жидкостью или газом. Движение жидкости – установившееся, подчиняется закону Дарси и является плоским. Плоское движение означает, что течение происходит в плоскостях, параллельных между собой, и картина движения во всех плоскостях идентична. В связи с этим разбирается течение в одной из этих плоскостей – в основной плоскости течения.
7.1. Метод суперпозиции (потенциалов)
Решение задач будем строить методом суперпозиции (наложения) потоков и методами теории функций комплексного переменного.

Метод суперпозиции заключается в следующем.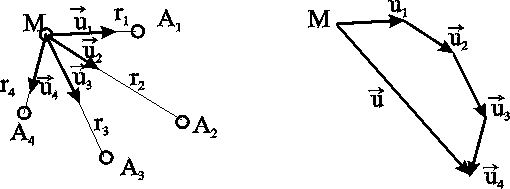




а б

Рис. 7.2. Схема векторного сложения скоростей фильтрации в произвольной точке М при работе нескольких источников и стоков
При совместном действии в пласте нескольких стоков (эксплуатационных скважин) или источников (нагнетательных скважин) потенциальная функция, определяемая каждым стоком (источником), вычисляется по формуле для единственного стока (источника). Потенциальная функция, обусловленная всеми стоками (источниками), вычисляется путём алгебраического сложения этих независимых друг от друга значений потенциальной функции. Суммарная скорость фильтрации определяется как векторная сумма скоростей фильтрации, вызванная работой каждой скважины (рис.7.2b).

Пусть в неограниченном пласте действует n стоков с положительным массовым дебитом Gи источников с отрицательным дебитом (рис. 7.2a).. Поток в окрестности каждой скважины в этом случае плоскорадиален и потенциал

, (7.1)

где i – номер скважины; r_i – расстояние между некоторой точкой пласта М и центром скважины под номером i.

Пользуясь методом суперпозиции, определяем потенциал сложного потока:

, (7.2)

где .

Зависимость (7.2) физически означает, что фильтрационные потоки от работы каждого источника-стока накладываются друг на друга. Так как. пласт предполагается неограниченным, то потенциал на бесконечности равен бесконечности. В центрах стоков-источников (r_i=0) потенциал также равен бесконечности.

Если жидкость несжимаема, то в зависимости (7.2), вместо массовых дебитов, можно использовать объёмные дебиты Q.

Для определения уравнений эквипотенциальных поверхностей (изобар) следует иметь в виду, что во всех точках этих кривых значение потенциала (давления) должно оставаться неизменным. Таким образом, приравнивая (7.2) к некоторой постоянной, получаем:

, (7.3)

где П – знак произведения; С₁ – постоянная.

Если дебиты всех скважин равны по величине, то

, (7.4)

где обозначение sign означает знак параметра G_i .

Линии тока образуют семейство кривых, ортогональных изобарам.

Метод суперпозиции можно использовать не только в бесконечных пластах, но и в пластах, имеющих контур питания или непроницаемую границу произвольной формы. В этом случае для выполнения тех или иных условий на границах вводятся фиктивные стоки или источники за пределами пласта. Фиктивные скважины, в совокупности с реальными, обеспечивают необходимые условия на границах, и задача сводится к рассмотрению одновременной работы реальных и фиктивных скважин в неограниченном пласте. Данный метод называется методом отображения источников и стоков.

Формула (7.2) – основная в решении задач интерференции скважин. Рассмотрим применение этой формулы в случаях: фильтрационного потока от нагнетательной скважины к эксплуатационной; пласта с произвольным контуром питания, но удалённым от скважин и пласта с прямолинейным контуром питания.
7.1.1. Фильтрационный поток от нагнетательной скважины к эксплуатационной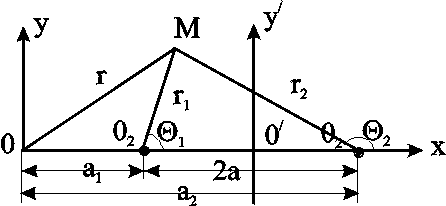



Рис. 7.3. Схема расположения источника 0₁ и стока 0₂
Пусть сток О₁ и источник О₂равнодебитны, т.е. имеют одинаковые по модулю массовые дебиты G. Расстояние между источником и стоком равно 2а. Исследуем поток от источника к стоку.

Проведём ось 0х через точки О₁ и О₂ таким образом, чтобы точка О₁ находилась от начала координат 0 на расстоянии а₁, а точка О₂ на расстоянии а₂ (рис. 7.3).

По формуле (7.2) определим потенциальную функцию потока. При этом учтем знаки дебитов: источник G₁= - G, а сток G₂= + G. После подстановки получим

, (7.5)

где r₁ и r₂ – расстояния любой точки пласта до стока и источника, соответственно.

Уравнение изобар (7.4) при этом будет иметь вид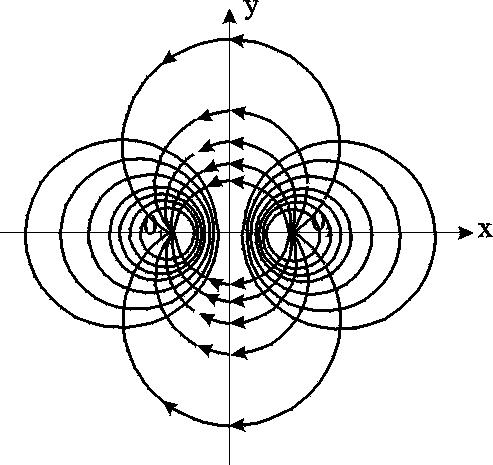

(7.6)




Рис. 7.4. Фильтрационное поле источника и стока
и соответствует окружностям, центры которых расположены на прямой, проходящей через центры скважин (рис.7.4). Среди окружностей есть одна, имеющая бесконечно большой радиус – прямая, которая делит расстояние между скважинами и всю плоскость течения пополам. Половина всех окружностей конечного радиуса расположена по одну сторону от этой прямой, остальные окружности - по другую.

Семейство линий тока ортогонально изобарам и, следовательно, в данном случае тоже окружности. Все линии тока проходят через сток и источник. Центры всех окружностей линий тока расположены на прямой, делящей расстояние между стоком и источником пополам (рис.7.4).

Массовый дебит эксплуатационной и нагнетательной скважин при их совместной деятельности определяется на основе соотношения (7.5), расписанного для каждой скважины при учете отношений радиусов (рис.7.3): на контуре эксплуатационной скважины – 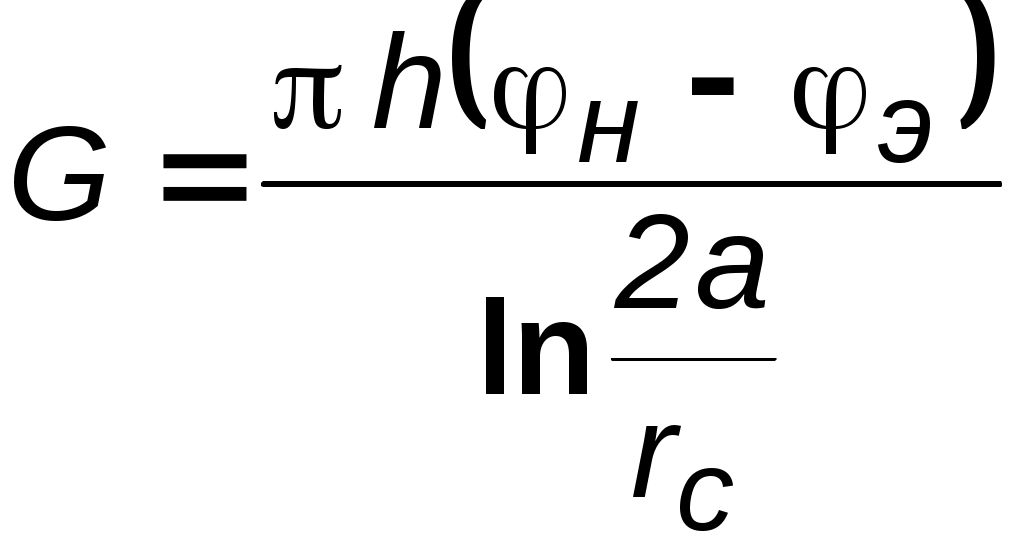; на контуре нагнетательной скважины – . Решая, полученную систему уравнений, имеем

. (7.7)

Массовая скорость фильтрации в любой точке пласта M (рис.7.2) находится по правилу суперпозиции сложения векторов скорости от действия источника и стока

Модуль массовой скорости i-ой скважины равен

, (7.8)

/ , /
Для поддержания пластового давления часто используется нагнетание воды в пласт. Определим для однородной несжимаемой жидкости время движения частицы по кратчайшему пути между нагнетательной и эксплуатационной скважинами, то есть по оси 0х. При жестководонапорном режиме решается при этом вопрос о времени, прошедшем от начала закачки воды в пласт до начала её прорыва в эксплуатационную скважину.

Чтобы решить указанную задачу, выразим скорость в (7.8) через производную расстояния по времени и, поместив начало координат в сток О₁, проинтегрируем полученное уравнение по х от х₀до х. Тогда время движения частицы от некоторой точки х₀до точки х определится зависимостью

. (7.9)

Время обводнения Т, т.е. время прохождения частицы расстояния О₁О₂= 2а определится из (7.9), если принять х=0; х₀=2а

, (7.10)

где Q - объёмный дебит.

Зная Т, можно найти площадь обводнения , приравнивая объёмы TQ и mh. Откуда . (7.11)

Анализ формул (7.9) и (7.10) показывает, что расстояние, пройденное частицей за время Т от нагнетательной скважины до эксплуатационной, вдвое больше расстояния пройденного другой частицей за это же время в положительном направлении оси х.
7.1.2. Приток к группе скважин с удаленным контуром питания
В большинстве практических случаев контур питания находится довольно далеко. Поэтому решения данной задачи позволяют провести предварительную оценку однородных участков месторождений.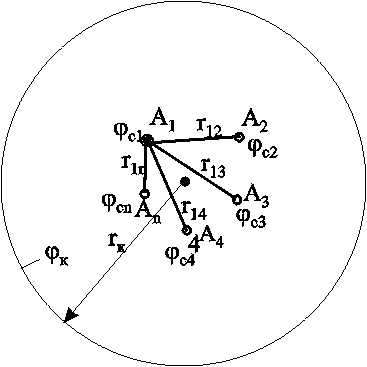




Рис. 7.5. Схема группы скважин в пласте с удаленным контуром питания
Пусть в пласте расположена группа из nскважин (рис. 7.5) с различными дебитами G_i, забойными потенциалами p_i и радиусами скважин r_i. Расположение скважин задано и на достаточно большом удалении находится контур питания, форма которого неизвестна, но известен порядок расстояния r_кот контура питания до группы скважин. При этом r_к намного больше расстояния между скважинами. Считаем, что потенциал контура _ки забойные потенциалыскважин _i. заданы.

Для определения дебитов используем формулу (7.2) при помещении точки М на забое каждой скважины, что позволяет записать n - уравнений вида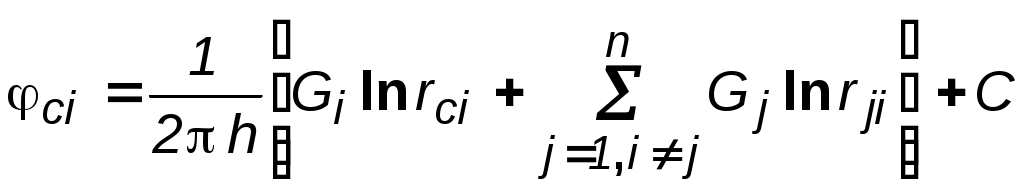

, (7.12)

где r_ci – радиус скважины, на которую помещена точка М; r_ji – расстояние между i - й и j - й скважинами; _ci – забойный потенциал i-й скважины.

Неизвестных же – n+1, так как константа С тоже неизвестна. Для нахождения С воспользуемся условием =_к на удалённом контуре питания:

. (7.13)

Приближение заключается в том, что для удаленных точек контура питания от скважин принимаем одно и то же расстояние r_к, что справедливо для достаточного удаления контура, учитывая, что оно находится под знаком логарифма. Уравнение (7.13) и будет (n+1) уравнением.

Таким образом, плоская задача интерференции при удалённом контуре питания сводится к решению алгебраической системы уравнений первой степени (7.12), (7.13).

При помощи данной системы можно находить или депрессию при заданном дебите, или получить значения дебитов при заданных депрессиях. При найденных дебитах можно определить пластовое давление в любой точке по (7.2), причем результат будет тем точнее, чем дальше эта точка отстоит от контура питания.
7.1.3. Приток к скважине в пласте с прямолинейным контуром питания
Пусть в полосообразном пласте пробурена одна скважина с центром в точке О₁ на расстоянии а от прямолинейного контура (ось у ) бесконечного протяжения, на котором поддерживается постоянный потенциал _к. На скважине радиуса r_cподдерживается постоянный потенциал _с.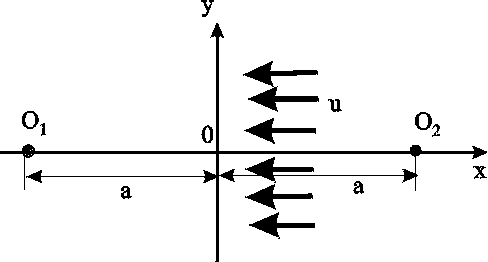




Рис. 7.6. Схема притока к скважине с прямолинейным контуром питания
Найдём дебит скважины Gи распределение функции . Так как контур питания пласта 0у является эквипотенциальной линией, то все линии тока, сходящиеся в центре скважины О₁, должны быть перпендикулярны к прямой 0у (рис.7.6). Для определения поля течения добьёмся выполнения граничных условий на контуре введением фиктивного источника О₂ с дебитом, равным дебиту стока О₁, путём зеркального отображения данного стока относительно прямой 0у.Таким образом, используем ранее упомянутый метод отображения и задачу о потоке в пласте с прямолинейным контуром питания и с одиночной эксплуатационной скважиной сведём к ранее рассмотренной в разделе 7.1.17. задаче о фильтрационном потоке от источника к стоку. Отличие данных задач только в постановке граничных условий: в задаче раздела 7.1.1. источник питания – нагнетательная скважина, а в данном случае – прямолинейный контур, а источник О₂ фиктивный.

Используем для определения дебита выражение (7.10), но со следующей заменой граничных условий:

 = _к при r₁ = r₂ ,т.е. при r₁/r₂ = 1;

 = _с при r₁ = r_с , r₂  2а, т.е. при r₁/r₂ r_с /2а.

Подставляя последовательно соответствующие граничные значения , r₁ и r₂ в равенство (7.10), получаем два уравнения, определяющих потенциалы на контуре и забое. Из этих уравнений легко находится массовый дебит одиночной скважины в пласте с прямолинейным контуром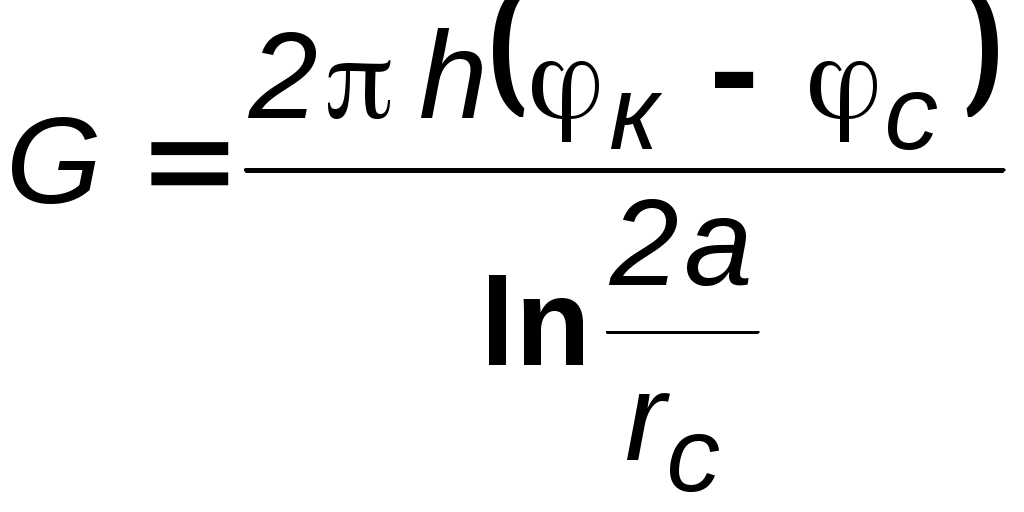

. (7.14)

Если бы в пласте была нагнетательная скважина, то в формуле (7.14) достаточно только изменить знак правой части.
7.1.4. Приток к скважине, расположенной вблизи непроницаемой прямолинейной границы
Данная задача может возникнуть при расположении добывающей скважины вблизи сброса или около границы выклинивания продуктивного пласта. В этом случае реальную скважину-сток зеркально отображают относительно непроницаемой границы, и дебиту скважины - отображения приписывают тот же знак, что и дебиту реальной скважины. При притоке к двум равнодебитным скважинам скорость фильтрации на непроницаемой границе будет направлена вдоль границы, т.е. граница является линией тока и фильтрация через неё отсутствует. Дебит скважины определяется из уравнений (7.12) и (7.13) для n=2 в пласте с удалённым контуром питания: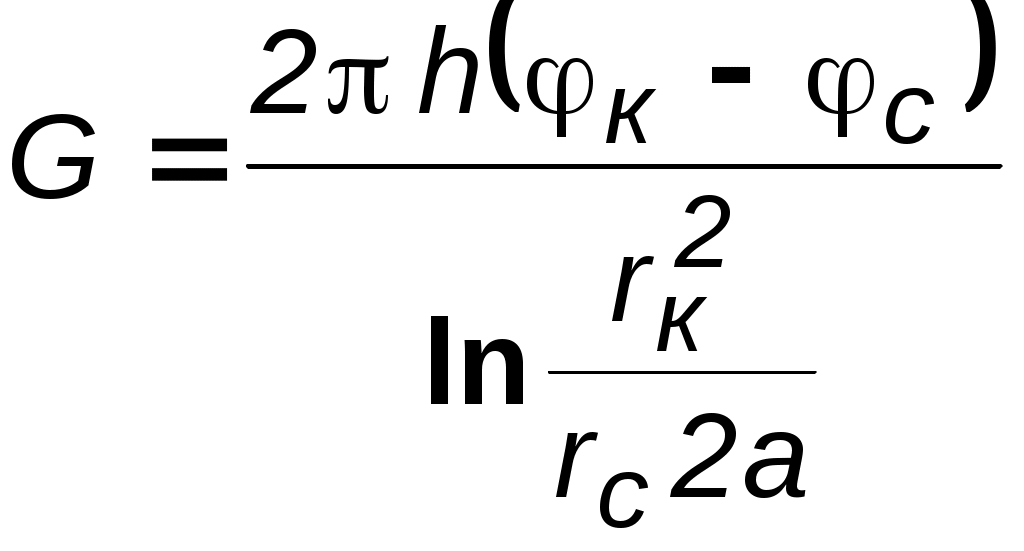

. (7.15)
7.1.5. Приток к скважине в пласте с произвольным контуром питания
В естественных условиях контур питания имеет произвольную форму и её не всегда удаётся определить. Кроме того, часто не удаётся определить достаточно точно и расстояние а от скважины О₁ до контура. Можно ли в этом случае пользоваться формулой предыдущего раздела? Любой произвольный контур В находится между прямолинейным В_пр и круговым В_кр (рис.7.7).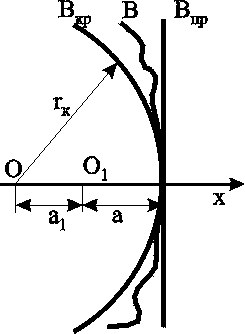



Рис.7.7. Схема видов

контуров питания
Расчеты дебитов, проведенные для этих двух крайних разновидностях контуров, показывают:

1. 
   При вычислении дебита скважины форма внешнего контура пласта не имеет сколько-нибудь существенного значения.
   
2. 
   Чем дальше от внешнего контура пласта находится скважина, тем меньший дебит она имеет. Однако так как величина расстояния входит под знаком логарифма, то даже значительное изменение этого расстояния мало влияет на величину дебита
   
3. 
   В случае расположения скважины эксцентрично относительно контура поток можно считать плоскорадиальным и дебит рассчитывать по формуле Дюпюи, если r_к.>10³r_cи эксцентриситет а₁< r_к /2.
   

Таким образом, для практических расчетов точное знание формы и расстояния до контура питания необязательно, но порядок расстояния до контура питания должен быть известен.