Подземная гидромеханика

• Название: Подземная гидромеханика
• Дата: 30.11.2022
• Размер: 3.56 Mb.
• Имя файла: Posobie_PGM.doc
• Тип: Учебное пособие; #820975
• страница: 16 из 17

II. b) Пусть характеристическая функция имеет вид:

, (8.22)

где а = а₁+ ia₂.

Это значит, что особая точка, в которой помещается точечный сток или точечный источник, сдвинута в направлении оси 0х на расстояние а_1., а в направлении оси 0yна расстояние a₂, и следовательно, центр поперечного сечения скважины находится не в начале координат, а в точке а = а₁+ ia₂.

Если представить комплексное переменное z-а в полярных координатах, то получим

, (8.23)

где r – расстояние любой точки плоскости потока не до начала координат, а до особой точки а = а₁+ ia₂, в которой помещается сток или источник; θ– полярный угол с вершиной в этой особой точке.

В соответствии с формулами (8.15) и (8.23)

(8.24)

Примечание. Потенциальная функция  и функция тока  определяются с точностью до произвольной постоянной. В формулах (8.24), выражающих  и , опущены произвольные постоянные, но их надо учитывать при определении дебита.
III. Пусть в основной плоскости течения имеется несколько точечных стоков и источников (несколько эксплуатационных и нагнетательных скважин).

Потенциальную функцию течения, поддерживаемого всеми стоками и источниками , можно определить по методу суперпозиции, описанному в параграфе 8.1, как алгебраическую сумму потенциальных функций течений, поддерживаемых отдельными стоками и источниками, если бы каждый из них был единственным в пласте.

На основании первого равенства (8.24) запишем

, (8.25)

где G_j– массовый дебит стока или источника за номером j; r_j – расстояние любой точки плоскости потока до этого стока или источника; n – число стоков и источников.

Метод суперпозиции основан на известных свойствах уравнения Лапласа, которому подчиняется потенциал , а именно, сумма частных решений уравнения Лапласа есть решение этого уравнения.

В то же время существование потенциальной функции _j означает существование наряду с ней функции тока _j,соответствующей каждому стоку и источнику. Функция _jудовлетворяет уравнению Лапласа; следовательно, по отношению к функции тока можно применять метод суперпозиции. Функция тока  для течения, поддерживаемого всеми стоками и источниками, определится аналогично потенциалу сложного потока:

. (8.26)

Характеристическая функция сложного потока, согласно формулам (8.1), (8.25, 8.26), определится уравнением:

(8.27)

где F_j(z) – характеристическая функция, соответствующая стоку или источнику за номером j, находящемуся в точке а_j-:

. (8.28)

8.4. Характеристическая функция течения при совместном действии источника и стока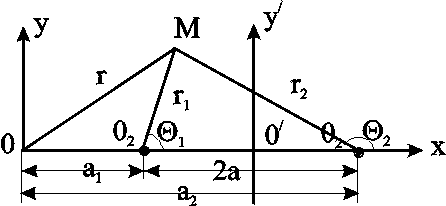


Рис. 8.5. Схема расположения источника 0₁ и стока 0₂
В разделе 7.1.6. подробно исследовалось семейство изобар в случае потока от нагнетательной скважины к эксплуатационной. О линиях тока было замечено, что они образуют семейство окружностей, ортогональных изобарам. Уточним вопрос об особенностях семейства линий тока на основе метода теории функций комплексного переменного.

Сохраняя прежние обозначения и придерживаясь рис. 8.5, получим на основании формул (8.27) и (8.28) характеристическую функцию течения от нагнетательной скважины к эксплуатационной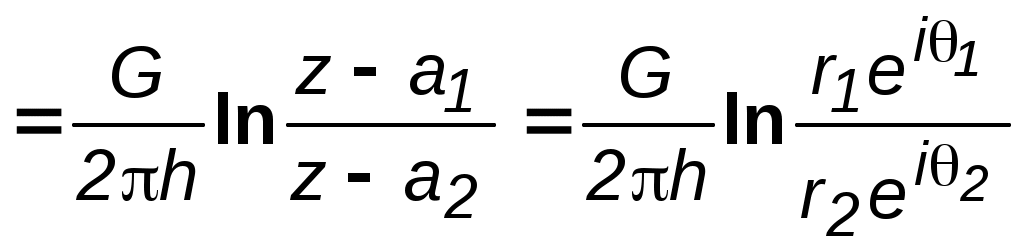

. (8.29)



где r₁и r₂– расстояния некоторой точки М до источника 0₁ и стока 0₂ , соответственно, θ₁ и θ₂ – соответствующие полярные углы; М – модуль массового дебита стока и источника.

Отделяя в (8.29) действительную часть от мнимой, получим

, (8.30)

Отсюда:

, (8.31)

Из (8.31) следует, что уравнение семейства изобар запишется в виде

,

где С – постоянное.

Уравнение линий тока получается из второй формулы (8.31):

θ₁-θ₂=С^*, (8.32)

где С^* – постоянное.

Рассмотрим уравнение (8.32). Выразим θ₁ и θ₂ через координаты точки М (х, у) в соответствии с рис. 8.23.

.

Подставив значения θ₁ и θ₂ в уравнение (8.32) и учитывая, что а₂-a₁=2a, будем иметь после несложных алгебраических преобразований:

(8.33)



где С^** - новая постоянная.

Из (8.33) видно, что центры окружностей имеют координаты 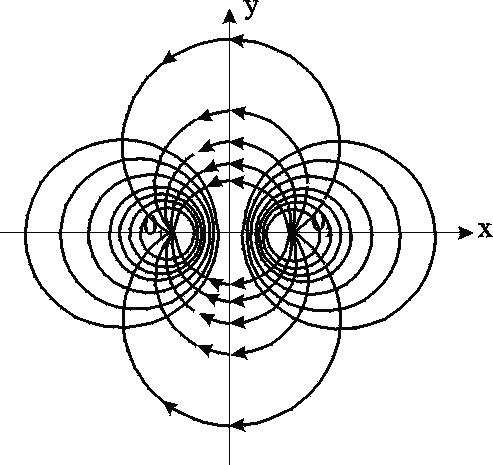. Так как абсцисса центров окружностей не зависит от С^**, то она одинакова для всех окружностей и, следовательно, все окружности расположены на прямой , То есть на прямой, параллельной оси 0у, делящей расстояние между стоком и источником пополам. Радиус окружностей .




Рис. 8.4. Фильтрационное поле источника и стока
Отсюда абсциссы точек пересечения



то есть линии тока проходят через сток и источник.

Таким образом, линии тока представляют собой окружности, проходящие через центры обеих скважин, и ортогональны окружностям - изобарам. Центры всех этих окружностей расположены на прямой (эквипотенциальной линии), делящей расстояние между скважинами пополам (рис. 8.6).


8.5. Характеристическая функция течения для кольцевой батареи скважин
Характеристическую функцию для пстоков представим в виде:

. (8.34)

Согласно формуле (8.28), можно записать

. (8.35)

Здесь а_j – комплексное число, определяющее положение стока за номером j.

В соответствии с формулой (8.14) комплексное число а_jможно представить в тригонометрической форме, заменив в (8.14) z на а_j, rна а (радиус батареи). Тогда формулу (8.35) можно переписать для кольцевой батареи из nскважин в следующем виде: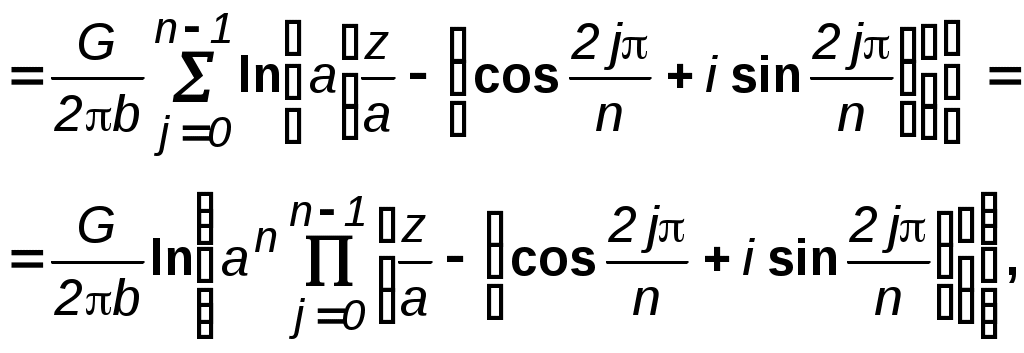

(8.36)



где .

Целая рациональная функция вида х^п- 1 может быть представлена в виде

. (8.37)

Выражение, сходное с правой частью формулы (8.37) имеется под знаком логарифма в (8.36). Таким образом, можно представить характеристическую функцию F (z) (8.36) в виде:

. (8.38)

Согласно формулам (8.9) и (8.38) находим модуль массовой скорости фильтрации :

, (8.39)

где z = re^i; r₁, r₂, ..., r_n – расстояния точки пласта от стоков O₁, О₂ , ...О_n– соответственно.

В центре кольцевой батареи r = 0. Из (8.39) следует, что скорость фильтрации uздесь равна нулю. Эти точки фильтрационного поля называются точками равновесия. При разработке залежей нефти в окрестностях таких точек образуются «застойные области» – «целики нефти».

Зная положения точек равновесия в пласте, можно находить рациональные приемы для своевременной ликвидации целиков нефти. Одним из таких приемов является изменение режима работы скважин, заставляющее нефть целика прийти в движение в нужном направлении.
ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. 
   Уравнения Коши-Римана.
   
2. 
   Потенциальная функция и функция тока.
   
3. 
   Характеристическая функция течения (комплексный потенциал).
   
4. 
   Связь проекций массовой скорости с потенциалом и функцией тока.
   
5. 
   Физический смысл функции тока.
   
6. 
   Характеристическая функция прямолинейно-параллельного потока.
   
7. 
   Характеристическая функция плоскорадиального потока.
   
8. 
   Характеристическая функция эксценnрично расположенной скважины.
   
9. 
   . Характеристическая функция группы скважин.
   
10. 
    . Характеристическая функция источника и стока.
    
11. 
    Характеристическая функция для кольцевой батареи скважин.
    

9. ОСНОВЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Теория разработки нефтегазовых месторождений располагает обширным арсеналом алгоритмов решения различных фильтрационных задач, которые призваны учитывать все основные особенности геологического строения месторождения и процессов, протекающих в пласте при добыче углеводородных флюидов. В большинстве случаев прикладные задачи разработки не имеют аналитического решения и требуют использования численных методов с применением ЭВМ.

В основе всех современных методов прогнозирования показателей разработки месторождений природных углеводородов лежат численные методы интегрирования соответствующих дифференциальных уравнений в частных производных, описывающих процессы двухмерной или трехмерной многофазной фильтрации. Численные методы, реализуемые на мощных ЭВМ, позволяют осуществлять широкомасштабные математические эксперименты и выполнять имитационное моделирование.

Математические эксперименты на ЭВМ используются в повседневной практике для исследования возможностей и эффективности новых технологий разработки, уточнения закономерностей тех или иных процессов. Воспроизведение на ЭВМ результатов лабораторных экспериментов позволяет затем на основе соответствующего алгоритма понять основные закономерности изучаемого процесса в макрообъеме, т. е. в масштабе всего месторождения. Такие обобщения нельзя получить на основе лабораторных экспериментов. Ожидание же завершения натурных экспериментов требует многих лет, а получаемые результаты, как правило, осложнены побочными, иногда необнаруженными факторами. Поэтому математические эксперименты на ЭВМ все в большем объеме используются для обоснования новых технологиче­ских решений, способствующих ускоренному внедрению достижений научно-технического прогресса.

Создание комплексных адаптирующихся геолого-математических моделей разработки конкретных месторождений представляет собой соединение возможностей теории с потребностями практики. Эти модели постоянно адаптируются на получаемую в процессе разработки фактическую информацию. Поэтому они позволяют уверенно осуществлять прогнозные расчеты. Вместе с тем они дают большие возможности для имитационного моделирования. Это означает, что на ЭВМ оценивается эффективность последствий от тех или иных шагов в тактике и стратегии разработки рассматриваемого месторождения природных углеводородов. Сегодня теория разработки месторождений природных углеводородов, базирующаяся на широком использовании ЭВМ, стала неотъемлемой частью любого проекта разработки месторождений углеводородов, а также мониторингового процесса.
8.1. Сущность математического моделирования
Сущность моделирования процессов фильтрации флюидов в пластах заключается в определении количественной связи между дебитами и давлениями на забоях скважин и определенных контурах, скоростей и сроков перемещения отдельных частиц пластовой жидкости в зависимости от формы залежи, параметров пласта, вязкости флюидов, числа и расположения скважин.

При решении фильтрационных задач можно выделить прямые и обратные задачи.

Прямые задачи – задачи, в которых свойства пласта и жидкостей, а также «начальные и граничные» условия считаются известными.

Прямые активные задачи – задачи определения полей давлений, нефтенасыщенности и водонасыщенности в нефтяном пласте – объекте разработки с системой скважин. Знание этих полей позволяет рассчитывать технологические показатели работы нефтяных и нагнетательных скважин.

Прямые пассивные задачи – определение конфигурации подвижной границы нефтяной зоны и скорости ее продвижения с целью установления сроков прорыва вытесняющего флюида в скважины и вычисления текущего коэффициента нефтеотдачи.

В одножидкостной модели определение подвижной границы сводится к прослеживанию линии отмеченных частиц в однородной жидкости. Для решения задачи оценки скорости продвижения контура нефтеносности используются поле пластовых давлений, поле проницаемости, текущее положение контура водо-нефтяного контакта. Скорость оценивается картой линий тока. Сгущение изолиний на картах равных значений пластового давления (карты изобар) может быть вызвано двумя причинами: ухудшением проницаемости и увеличением скорости отбора жидкости скважинами. Эти два фактора можно разделить, если учесть продуктивность скважины: высокая продуктивность связана с хорошей проницаемостью пласта. По наборам карт изобар могут быть определены параметры гидропроводности и проницаемости.
Наряду с прямыми задачами важное практическое значение имеют так называемые обратные задачи. Среди можно выделить «пассивные» и «активные» обратные задачи.

Решение «пассивных» обратных задач направлено на распознавание объектов разработки и позволяет уточнять представления о состоянии и свойствах пластовой системы.

«Активные» обратные задачи – задачи управления, регулирования процесса разработки пласта или месторождения.
Математическая модель является идеализированным представлением реального месторождения, так как затруднен учет объективно имеющихся несовершенств:

• 
  нехватки исходных данных для моделирования,
  
• 
  зональной и послойной неоднородности,
  
• 
  многофазности фильтрационных потоков,
  
• 
  нелинейности законов фильтрации,
  
• 
  нестационарности процессов,
  
• 
  различий свойств нефти и вытесняющего агента,
  
• 
  капиллярных и гравитационных сил,
  
• 
  частичной негерметичности скважин,
  
• 
  отклонения забоев скважин от проектных,
  
• 
  ограниченной долговечности скважин и случайного их выбытия,
  
• 
  неопределенности фактического пластового давления,
  
• 
  угрозы оттока нефти от эксплуатационных скважин и ее потерю,
  
• 
  ухудшения продуктивности нефтяных слоев при снижении забойного давления скважин ниже давления насыщения и других..
  

При математическом моделировании необходимо также учитывать порядок разбуривания, систему размещения и режимы работы скважин, их интерференцию, наличие водонасыщенных и газонасыщенных зон пласта и другие факторы.
Несмотря на имеющиеся сложности, математическое моделирование получило широкое распространение в практике построения постоянно действующих геолого-технологических моделей нефтяных резервуаров, разрабатываемых системами скважин. Известно достаточно много коммерческих систем и технологий такого назначения. Однако существуют глобальные общепризнанные проблемы, свойственные большинству исследовательских и коммерческих программных систем – «симуляторов» (от английского «simulation» – моделирование). Они будут рассмотрены ниже.

Движущиеся в пласте флюиды неоднородны. При моделировании процессов вытеснения нефти водой при давлениях, выше давления насыщения нефти газом, достаточно использовать двухфазную математическую модель. При моделировании разработки нефтегазовых залежей при существенном влиянии гравитационного разделения фаз на процесс разработки, при прогнозировании эффективности процесса закачки воды и газа необходима модель трехфазной фильтрации нефти, газа и воды. Для расчета процесса разработки газоконденсатных пластов, оценки эффективности отдельных методов увеличения нефтеотдачи пластов необходимо рассматривать нефть как смесь углеводородных компонентов, т.е. использовать композиционные модели.
Обязательным элементом технологии компьютерного моделирования нефтегазовых резервуаров является процедура адаптации математической модели к известной истории разработки месторождений и работы скважин. Она состоит в согласовании результатов расчетов технологических показателей предшествующего периода разработки с фактической динамикой разбуривания объектов, добычи нефти, закачки воды, пластовых и забойных давлений, обводненности продукции скважин и газовых факторов. В результате такого согласования математическая модель, используемая для прогноза коэффициента нефтеизвлечения и технологи­ческих показателей, идентифицируется с реальными параметрами пласта. Адаптация модели позволяет уточнить фильтрационные и емкостные параметры пласта, функции относительных фазовых проницаемостей для нефти, газа и воды, энергетические характеристики пласта – поля давлений, оценки выработки запасов нефти на отдельных участках пластов. В результате адаптации модели уточняются размеры законтурной области, начальные и остаточные геологические запасы нефти и газа, проницаемость и гидропроводность пласта, коэффициенты продуктивности и приемистости, функции модифицированных фазовых проницаемостей, функции адсорбции, десорбции.
Для построения геологических и фильтрационных моделей, адекватных реальным объектам, необходим большой объем достоверных исходных данных. Все известные зарубежные компьютерные системы моделирования исходят из наличия таких данных.

Так, для построения геологических моделей необходимы данные сейсморазведки и их интерпретации, результаты анализов и исследований кернов, результаты исследований промысловой геофизики, их интерпретации, данные инклинометрии скважин, сведения о составах и минерализации грунтовых вод и т.д.

Для построения фильтрационных моделей необходимы результаты интерпретации геофизических исследований скважин, помесячная история разработки месторождений, координаты скважин и режимы их работы, значения пластовых и забойных давлений в скважинах и другая информация.
Математическая модель состояний нефтяных резервуаров и процессов в них является основной компонентой так называемых постоянно действующих геолого-технологических моделей. По современным понятиям, такие постоянно действующие геолого-технологические модели должны объединять следующие подсистемы:

• 
  базу данных геолого–геофизической и промысловой информации;
  
• 
  программные средства геометризации залежей нефти и подсчета балансовых запасов нефти;
  
• 
  геолого–математическую модель месторождения (залежей);
  
• 
  математические модели процессов разработки;
  
• 
  программные средства адаптации математических моделей по из­вестной истории разработки;
  
• 
  программные средства оптимизации процесса и систем разработки по заданным технологическим и экономическим критериям;
  
• 
  базы знаний и экспертных систем для принятия решений по управ­лению процессом разработки;
  
• 
  программные системы формирования отчетов и визуализации инфор­мации в форме карт, графиков, диаграмм и результатов их интерпретации.
  

Недостаточный объем и низкое качество информации позволяют рассматривать модель процесса разработки лишь как наиболее правдоподобную при этой исходной информации. Если не планируются детальный сбор и анализ геолого-промысловой информации или ставится задача только краткосрочного прогноза технологических показателей, то применение «постоянно действующей модели» нецелесообразно и вполне оправдано использование более простых программных средств.

Основными тенденциями моделирования являются учет тонких эффектов различной природы, сопутствующих процессам фильтрации, путем построения разномасштабных моделей с рассмотрением внутренней структуры процессов; построение полномасштабных математических моделей функционирования пластов без их поблочного рассмотрения; исследования в области непознанных пока явлений.
9.2. Основные проблемы гидродинамического моделирования
Известно, что энергетическое состояние нефтяного или нефтегазового резервуара характеризуется полем давлений, а градиент давлений является основной движущей силой процессов фильтрации флюидов. Поэтому расчет и анализ полей давлений – обязательные атрибуты гидродинамического моделирования. Поля давлений, направления и скорости фильтрации флюидов необходимо также анализировать при выборе гидродинамических регулирующих воздействий и других методов повышения нефтеотдачи, включая гидроразрыв пласта, а также при проектировании и бурении вертикальных и наклонных, горизонтальных и многозабойных горизонтально - ветвящихся скважин.

Расчет полей давлений в резервуарах с произвольными системами гидродинамически взаимосвязанных скважин различных профилей представляет существенные трудности для большинства вычислительных методов и их программных реализаций. Эти трудности еще более возрастают при решении задач для резервуаров с тектоническими нарушениями.
При решении задач математического моделирования полей давлений в нефтяных резервуарах с системами скважин используются две технологии:

• 
  Инженерный подход к формированию и анализу карт изобар, который может быть реализован вручную или с привлечением компьютерных технологий. В условиях реального нефтедобывающего производства карты изобар являются регламентными и формируются с периодичностью 3–6 месяцев. По ним производится оперативный анализ падения и роста давлений в отдельных зонах пласта, оцениваются скорости и направления фильтрации флюидов с возможными перемещениями контуров нефтеносности, производится расчет средневзвешенных пластовых давлений по объемам или площадям зон отбора, нагнетания и всей залежи, а также для блоков блочных систем разработки. Процедуру формирования карт изобар можно условно отнести к графо -аналитическим методам моделирования полей давлений.
  

Одна из основных проблем использования такого метода исследования – низкая информативность используемых исходных данных. В самом деле, для расчетов и построений карт изобар в качестве исходных данных используются, в основном, результаты обработки гидродинамических исследований специально останавливаемых скважин. Однако, сознательно недобирая остановленными скважинами нефть, за период 3 – 6 месяцев удается оценить пластовые давления не более чем для 25 – 40% всего работающего фонда скважин. По этим накопившимся данным и формируется карта изобар в предположении, что все данные получены одновременно и адекватно характеризуют состояние резервуара на день её построения.

Другая группа проблем связана с применяемыми методами расчета. Формирование карт изобар обычно сводится к решению классической задачи вычислительной математики – интерполяции значений математической функции – пластовых давлений, заданных в нерегулярно расположенных точках – скважинах. Однако известные методы интерполяции сплайнами, полиномами и т.п. здесь не вполне годятся, так как получаемые результаты зачастую противоречат физическому смыслу решаемой задачи. Так, например, при использовании таких формальных методов можно получить локальные максимумы пластовых давлений между нагнетальными скважинами, а минимумы – между нефтяными скважинами, но не в них. Поэтому на практике обычно используются более простые и надежные, но менее совершенные методы, основанные на триангуляции расчетной области.

Такое графо-аналитическое моделирование затруднено для горизонтальных и горизонтально-ветвящихся скважин, для скважин с трещинами гидроразрыва пласта, для пластов с тектоническими нарушениями. Оно неадекватно отражает поле давлений в системе работающих скважин, где изменения пластовых давлений между нефтяными и нагнетательными скважинами, в соответствии с теорией фильтрации, изменяются по логарифмическому закону и существуют «воронки депрессии», «воронки регрессии». Заметим, что и проведение даже самого простого вычислительного эксперимента, например, какое будет поле давлений, если изменить режим работы одной или нескольких скважин, по этой технологии также невозможно.

• 
  Математическое моделирование процессов фильтрации в нефтяном резервуаре с системой нефтяных, нагнетательных, пьезометрических и других скважин. Такое моделирование имеет значительно более широкие возможности и состоит в постановке и решении систем дифференциальных уравнений, описывающих процессы многофазной фильтрации флюидов в пористой среде. Решение производится одним из численных методов – обычно методом конечных разностей или конечных элементов. Такое моделирование производится в условиях научных или проектных организаций с использованием исследовательских или коммерческих версий соответствующих программных систем. Они являются системообразующим элементом так называемых постоянно действующих геолого - технологических моделей месторождений и остаются уникальными научно - техническими разработками, а их эксплуатация по-прежнему остается более искусством, нежели ремеслом.
  

Для математического моделирования необходим большой объем достоверных данных о геологической модели залежи, ее фильтрационных свойствах, порядке разбуривания, системе размещения, истории и режимах работы скважин, их интерференции, наличии водонасыщенных и газонасыщенных зон пласта и других факторах. Одним из основных результатов такого моделирования является расчетное поле пластовых давлений. Заметим, что расчет именно этих полей отнимает значительную часть вычислительных ресурсов компьютера: оперативную память и время работы процессора.
Основные проблемы математического моделирования полей пластовых давлений в нефтяных резервуарах с произвольными системами гидродинамически взаимосвязанных скважин:

1. Привлечение математического моделирования для решения задач оптимизации систем разработки нефтегазовых месторождений требует использования гидродинамических моделей, уровень детализации которых позволяет рассматривать скважину в качестве объекта управляющих воздействий. При этом становится возможным имитировать на моделях резервуара различные гидродинамические управляющие воздействия, связанные с изменением схем закачки и отбора жидкости скважинами: перенос фронта нагнетания, изменение направлений фильтрационных потоков, использование очаговых заводнений, перераспределение отборов по рядам скважин и участкам пласта, добуривание нагнетательных и эксплуатационных скважин, переход к более интенсивным системам разработки и др.

Вместе с тем для адекватного описания процесса эксплуатации месторождений, находящихся в разработке длительное время, необходимо иметь полноразмерные модели, способные имитировать работу большого числа гидродинамически взаимосвязанных скважин. Современные программные системы позволяют моделировать до 1500 – 2000 скважин, что становится недостаточно, так как ряд месторождений, например, Повховское, Мамонтовское, Самотлорское и другие месторождения Тюменской области имеют более 3500, 5000, 15000 скважин.

2. Интенсификация разработки нефтяной залежи может достигаться не только за счет создания более высоких градиентов давлений в системах нагнетательных и эксплуатационных скважин, но также и снижением фильтрационных сопротивлений в их призабойных зонах. Для этих целей могут использоваться бурение и эксплуатация скважин с повышенной поверхностью вскрытия продуктивного пласта: горизонтальные, наклонные, горизонтально - ветвящиеся или многозабойные. Большое разнообразие геолого - технических условий, различное состояние разработки месторождений, условия и способы эксплуатации требуют различных профилей, числа и протяженности стволов многозабойных скважин.

Для обоснованного применения горизонтальных и горизонтально–ветвящихся скважин и технологий разработки месторождений с их использованием необходимо исследование взаимодействия многозабойно - горизонтальных скважин как между собой, так и в системе с традиционными вертикальными и наклонно - ориентированными скважинами. В этих случаях расчет технологических показателей процессов разработки и моделирование фильтрационных процессов не могут быть выполнены при помощи обычных формул и моделей, применяемых для расчета взаимодействия более привычных вертикальных скважин. Поэтому создание теоретических основ проектирования разработки месторождений скважинами сложного профиля актуально и сводится, по существу, к разработке методов расчета дебитов и перепадов давлений в работе групп этих скважин.

3. Одним из наиболее эффективных методов повышения продуктивности скважин любого профиля в низкопроницаемых коллекторах является гидроразрыв пласта. При гидроразрыве в призабойных зонах нефтяных и нагнетательных скважин образуется одна или несколько вертикальных трещин, способствующих существенному снижению фильтрационных сопротивлений и увеличению притока жидкости.

Оценка эффективности и влияния гидроразрыва пласта на динамику обводнения скважин связана с анализом сложных фильтрационных процессов в окрестности скважин и вблизи высокопроводящих трещин сложных конфигураций с ускоренным продвижением флюидов по ним.

4. Для большего соответствия реальности математическое моделирование надо проводить для пластов сложных конфигураций, с нетривиальными условиями на внутренних и внешних границах пласта – контурах питания, при наличии тектонических и других нарушений в строении пластов.

5. Попытки учета вышеназванных факторов при математическом моделировании нефтегазовых резервуаров сталкиваются с общими проблемами используемых вычислительных методов.

Прежде всего, эти проблемы связаны с наличием у искомых решений соответствующих математических задач особых точек (в случае вертикальных и наклонно–ориентированных скважин), линий и кривых (для горизонтальных и горизонтально–ветвящихся скважин) или особых поверхностей (для фронтов вытеснения, различных геологических нарушений строения пласта, трещин гидроразрыва, образований макроцеликов).

Так, например, для сеточных методов расчета эти особенности побуждают сгущать расчетные сетки и требуют решения проблем пересечения особых линий и поверхностей нескольких ячеек разностной сетки под произвольными углами. Это затрудняет автоматизацию постановок и решений задач моделирования, приводит к увеличению времени счета и требуемого объема оперативной памяти компьютера, ограничивает сложность решаемых задач вплоть до принципиальной невозможности их решения данным методом.

Поэтому скважины сложного профиля, трещины гидроразрыва – объекты повышенной сложности для численного моделирования. Они требуют отказа от регулярных сеток и перехода к методам конечных элементов, граничных элементов, граничных интегральных уравнений и им подобным.

6. Математическое моделирование предполагает проведение вычислительных экспериментов. Они необходимы для многовариантных расчетов при адаптации (настройке) моделей по известной истории разработки месторождений и при решении оптимизационных задач. Поэтому методы расчета, алгоритмы и их программные реализации должны быть предельно быстрыми, а результаты математического моделирования должны быть надежными и физически содержательными. Это позволит математические модели использовать не только в исследовательских центрах, но и в условиях нефтедобывающего предприятия при формировании, например, карт изобар по ограниченному набору технологических параметров скважин – дебитов, приемистостей и давлений.

Сформулированные выше проблемы не могут быть решены инженерными методиками и трудноразрешимы в рамках привычных математических моделей, включая известные коммерческие программные системы типа ECLIPSE, MORE, VIP и др. Их решение возможно на пути разумных упрощений постановок задач, развития известных численных и численно - аналитических методов и разработки новых подходов.


ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. 
   Сущность моделирования процессов фильтрации флюидов в пластах.
   
2. 
   Прямые задачи.
   
3. 
   Обратные задачи.
   
4. 
   Прямые активные задачи.
   
5. 
   Прямые пассивные задачи.
   
6. 
   Обратные активные задачи.
   
7. 
   Обратные пассивные задачи.
   
8. 
   Причины необходимости идеализации математической модели.
   
9. 
   Область использования двухфазной математической модели.
   
10. 
    Область использования трехфазной математической модели.
    
11. 
    Область использования композиционной математической модели.
    
12. 
    Сущность адаптации математической модели к известной истории разработки месторождений и работы скважин.
    
13. 
    Что позволяет уточнить процесс адаптации?
    
14. 
    Какие данные требуются для построения геологических моделей.
    
15. 
    Какие данные требуются для построения фильтрационных моделей?
    
16. 
    Для чего нужен анализ полей давления и скоростей фильтрации?
    
17. 
    Инженерный подход моделирования полей давления.
    
18. 
    Определение поле давления путем математического моделирования процессов фильтрации.
    
19. 
    Основные проблемы математического моделирования полей пластовых давлений.
    

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Глава 1
Коллектора –это горные породы, которые могут служить хранилищами нефти, газа, воды и отдавать их при разработке.

Флюид – жидкость, газ, смесь жидкости и газа, то есть всякая текучая среда.

Теория фильтрации – наука, описывающая движение флюида с позиций механики сплошной среды, то есть гипотезы сплошности (неразрывности) течения.

Многофазные системы – два или больше флюида, занимают отдельные четко различимые объёмы (пузырьки газа в жидкости, капли или плёнки в газе) и взаимодействуют на поверхностях раздела.

Однофазные или гомогенные системы – многокомпонентные смеси (природный газ, нефть), в которых взаимодействие происходит на молекулярном уровне и поверхности раздела выделить нельзя.

Напряжение – нагрузка (трение соседних объёмов, внешние силы), отнесённая к единице площади.

Реологическое соотношение (закон) –- соотношение, связывающее деформацию или скорость изменения деформации с напряжением или его градиентом.

Закон Ньютона – , гдеu_x – скорость в направлении х; у – направление, перпендикулярное х; μ – коэффициент динамической вязкости.

Фиктивный грунт – среда, состоящая из шариков одного размера, уложенных во всем объёме пористой среды одинаковым образом по элементам из восьми шаров в углах ромбоэдра.

Идеальный грунт – среда, состоящая из трубочек одного размера, уложенных одинаковым образом по элементам из четырех трубочек в углах ромба.

Недеформируемая среда– объём пустот не изменяется или изменяется так, что его изменением можно пренебречь.

Упругая ( кулоновская) среда – деформируется с линейным изменением объёма от напряжения.

Пластичная (глины), текучая (несцементируемые пески) или разрушаемаясреда–деформируется с остаточным изменением объёма, т.е. линия нагружения не совпадает с линией разгружения.

Изотропия – независимость изменения физических параметров от направления.

Анизотропия – различные изменения по отдельным направлениям.

Полная пористость – отношение объема пор к общему объему элемента.

Просветность – отношение площади просветовко всей площади сечения образца.

Открытая пористость – отношение объема открытых пор к общему объему элемента.

Динамическая (эффективная) пористость – отношение объема, занятого подвижной жидкостью, к общему объему элемента.

Эффективный диаметр частиц – диаметр шаров, образующих эквивалентный фиктивный грунт, при котором гидравлические сопротивление, оказываемое фильтрующейся жидкости в реальном и эквивалентном грунте, равны.

Удельная поверхность – суммарная площадь поверхности частиц, содержащихся в единице объёма.

Насыщенность – отношение объёма данного флюида, содержащегося в порах, к объёму пор.

Связанность– отношение объёма, связанного с породой флюида, к объёму пор.

Проницаемость – параметр породы, характеризующий её способность пропускать к забою скважины флюиды.

Абсолютная проницаемость – свойство породы и не зависит от свойств фильтрующегося флюида и перепада давления, если нет взаимодействия флюидов с породой, характеризует площадь сечения каналов пористой среды, по которым происходит фильтрация.

Фазовая проницаемость – проницаемость пород для данного флюида при наличии в порах многофазных систем.

Относительная проницаемость – отношение фазовой проницаемости к абсолютной.

Трещиноватость – отношение объёма трещин ко всему объёму трещинной среды.

Густота трещин – отношение полной длинывсех трещин, находящихся в данном сечении трещинной породы к удвоенной площади сечения.

Раскрытость трещины – ширина трещины.

Скорость фильтрации – среднерасходная скорость, то есть скорость осреднённая по площади сечения породы.

Закон Дарси – линейный закон фильтрации, устанавливающий линейную связь между перепадом напора на единицу длины и объёмным расходом жидкости в грунте или горной породе.

Коэффициент фильтрации – коэффициент закона Дарси, характеризующий среду и жидкость одновременно, т.е. зависящий от размера частиц, от их формы и степени шероховатости, пористости среды, вязкости жидкости.

Критическая скорость фильтрации – скорость фильтрации, при которой нарушается закон Дарси.