Подземная гидромеханика

• Название: Подземная гидромеханика
• Дата: 30.11.2022
• Размер: 3.56 Mb.
• Имя файла: Posobie_PGM.doc
• Тип: Учебное пособие; #820975
• страница: 9 из 17

Анализ основной формулы теории упругого режима. Основная формула (4.19) или (4.23) строго говоря справедлива лишь для точечного стока, т.е. при r_с=0. Практические расчеты показывают, что ей можно пользоваться даже для укрупнённых скважин (r_с1км) и нельзя использовать только в первые доли секунды после пуска скважины. Если скважина укрупнённая, то формула (4.23) может дать большую погрешность лишь вблизи от её стенки (контура). Чем дальше отстоит от этого контура точка, в которой определяется давление, и чем больше времени прошло с момента пуска укрупнённой скважины, тем меньше погрешность.

Анализ формулы (4.23) показывает, что вскоре после пуска скважины вокруг неё начинает непрерывно увеличиваться область пласта (рис.4.2), в которой для каждого момента времени давление распределяется так, как и при установившемся движении, т.е. давление оказывается квазиустановившимся и пьезометрические кривые будут кривыми логарифмического типа.

Из (4.23) следует, что градиент давления, расход жидкости через любую цилиндрическую поверхность радиусом r и скорость фильтрации определяются соотношениями: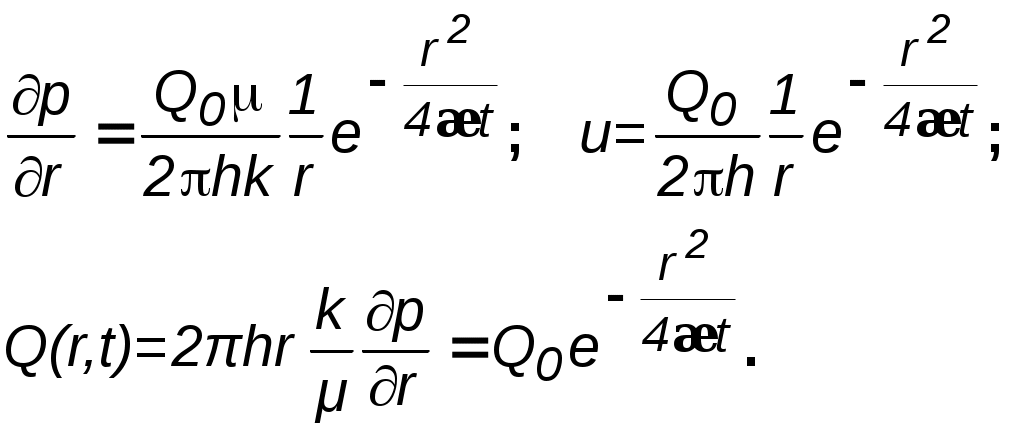

(4.24)

Из данных соотношений следует, что стационарная скорость достигается очень быстро на небольших расстояниях от скважины, так как значение коэффициента пьезопроводности велико.

4.1.5. Приток к скважине в пласте конечных размеров в условиях упруговодонапорного и замкнутоупругого режимов
Круглый горизонтальный пласт с открытой внешней границей
Постоянный дебит. Пусть пласт имеет внешнюю границу радиусом r_к, через которую может поступать вода при истощении упругого запаса. В центре пласта имеется скважина радиусом r_с, которая мгновенно запускается в эксплуатацию с постоянным дебитом Q₀. Перед пуском скважины давление в пласте было р_к.

Для определения давления используем полученную ранее зависимость для неограниченного пласта

, (4.19)

и формулу Дюпюи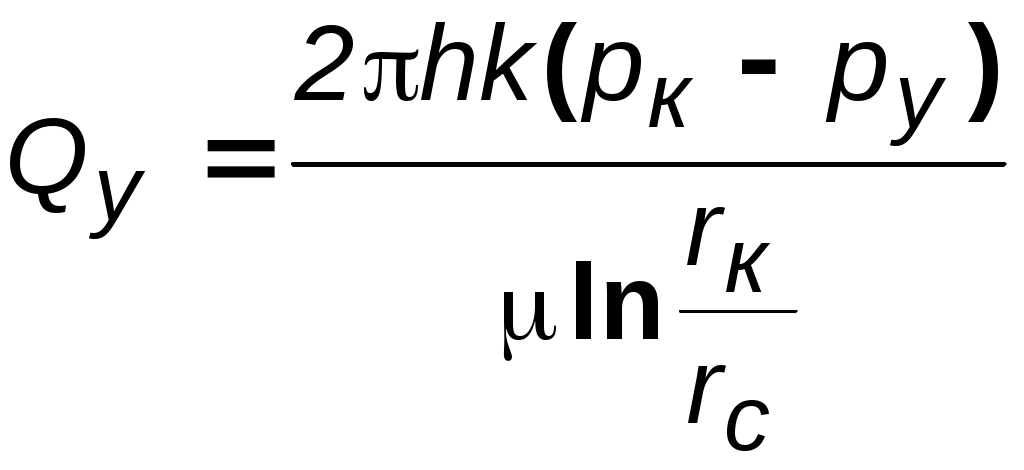

(4.25)

для установившегося плоскорадиального потока. В результате совместного решения данных зависимостей получим следующую приближённую формулу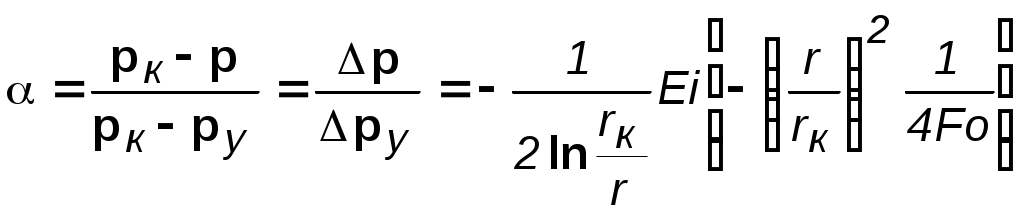

, (4.26)

где р_у – установившееся давление в любой точке пласта или в реагирующей бездействующей скважине (давление р_у соответствует времени t =  или Fo = ).

Изменение пьезометрической кривой в различные моменты времени после пуска скважины с постоянным дебитом в пласте с круговым контуром питания показано на рис.4.3а.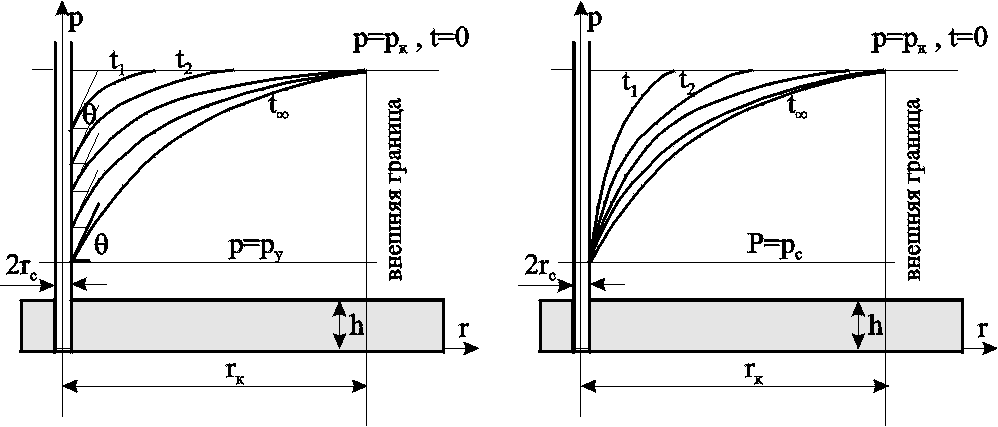



a b

Рис. 4.3. Пьезометрические кривые при пуске скважины в конечном пласте с открытой внешней границей:

а – с постоянным дебитом;

b – с постоянным забойным давлением р_с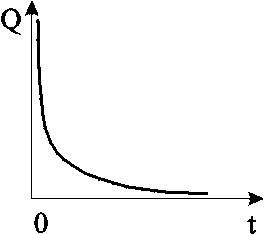




Рис. 4.4. Изменение дебита скважины с течением времени при постоянном забойном давлении р_с
Постоянное забойное давление. На рис 4.3b изображена в различные моменты времени пьезометрическая кривая после пуска возмущающей скважины с постоянным забойным давлением, на рис.4.4 – изменение дебита скважины с течением времени.

Круглый горизонтальный пласт с закрытой внешней границей
Постоянный дебит. Будем считать дебит скважины постоянным. Пьезометрические кривые падения давления для разных моментов времени показаны на рис. 4.5. С некоторого момента смещение во времени пьезометрической кривой для закрытого пласта происходит так, что все точки её опускаются на одно и тоже расстояние , т.е. во всех точках пласта давление падает с одной скоростью.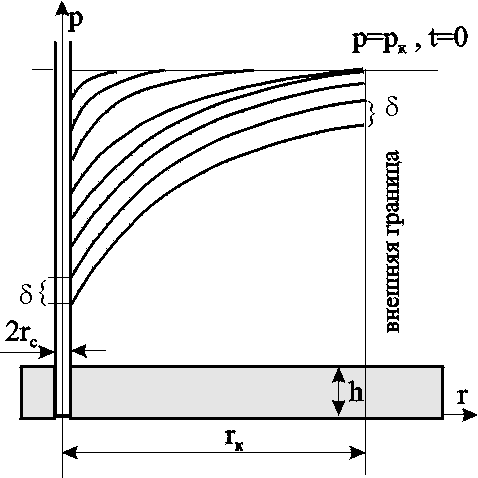



Рис. 4.5. Пьезометрические кривые при пуске скважины в конечном пласте с закрытой внешней границей при постоянном дебите
Из рассмотрения рис. 4.3, 4.5. видно, что в условиях упругого режима процесс перераспределения давления, а значит, и процесс взаимодействия скважин развивается постепенно, если же и наблюдается аномально быстрое взаимодействие скважин, то это можно объяснить неоднородностью пластов и их анизотропией.

Кроме того, при пуске или остановке скважины давление вначале меняется быстро, а затем темп изменения давления замедляется.

Если скважина действовала с постоянным дебитом при установившимся потоке и в некоторый момент времени она останавливается, то начинается процесс восстановления давления. Уровень жидкости в скважине начинает подниматься.

Для расчета используются полученные выше формулы для возмущающей скважины, но вместо данных понижения давления в пласте надо подставить данные повышения давления после остановки скважины.
Постоянное забойное давление. Объемный дебит возмущающей скважины определяется по формуле

(4.27)

а объем жидкости V_f, добытой из скважины (в пластовых условиях) за время t с момента пуска скважины равен .

При больших параметрах Фурье fo объем V_f оказывается равным упругому запасу жидкости в закрытом пласте

V_f  ^*(р_к - р_с). (4.28)

На рис. 4.6 показана пьезометрическая кривая для нескольких моментов времени в закрытом пласте, а на рис. 4.7 изображены две кривые: одна из них характеризует падение дебита скважины с постоянным забойным давлением (кр. 1); другая – рост суммарной добычи жидкости V_f (кр.2).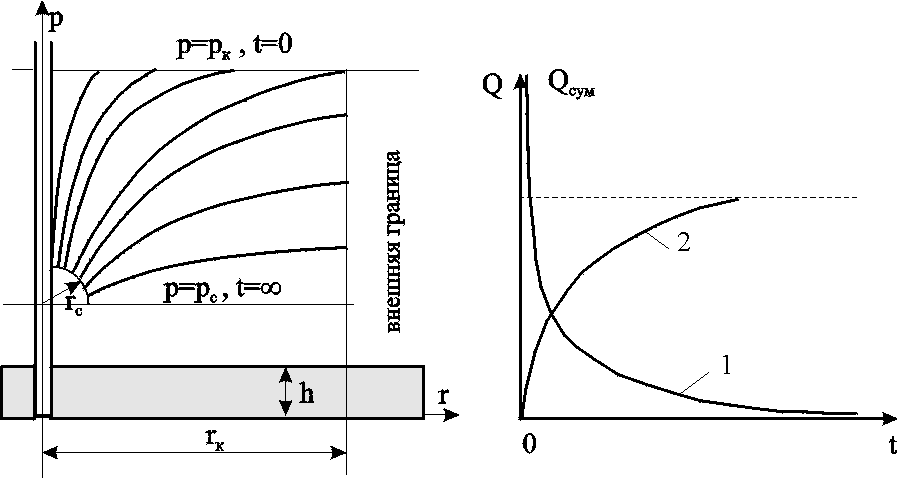





Рис. 4.6. Пьезометрические кривые при пуске скважины в конечном пласте с закрытой внешней границей при постоянном забойном давлении

Рис. 4.7. Изменение дебита Q (кр.1) скважины и суммарной добычи Q_cp (кр.2) с течением времениt


4.1.6. Периодически работающая скважина
В неограниченном пласте останавливается скважина, эксплуатирующаяся с постоянным дебитом Q в течении времени Т, сравнимого со временем проведения исследований. Понижение давления р в момент времени Т можно найти по формуле

(4.23).

С момента остановки давление в ней и окружающей области пласта повышается, т.е. с данного момента в одном и том же месте пласта как бы действуют совместно и непрерывно эксплуатационная (сток) и нагнетательная (источник) скважины. При этом источник имеет тот же дебит Q. Обозначим повышение давления за счет работы источника через р^//.. Таким образом, начиная с момента времени Т, на основании формулы (4.23) имеем:

, (4.29)

.

Результирующее понижение давления р в любой точке пласта находится по методу суперпозиции

. (4.30)

Обозначая через р_с давление на забое скважины после её остановки, получаем

. (4.31)

Зависимость (4.31) используется при гидродинамических исследованиях скважин, работающих не продолжительное время, методом построения кривой восстановления давления.
4.1.7. Определение коллекторских свойств пласта по данным исследования скважин нестационарными методами
Различают две группы гидродинамических методов: при установившихся и неустановившихся режимах. Первые связаны с теорией одномерного потенциального течения, а вторые – с теорией упругого режима. После пуска или остановки скважины происходит перераспределение давления, которое можно снять и получить кривую восстановления (КВД) или стабилизации (КСД) давления. На форму данных кривых влияют коллекторские свойства, что дает возможность определения таких параметров как проницаемость и пьезопроводность.

Наиболее распространен метод определения коллекторских свойств по данным о восстановлении забойного давления (КВД) в остановленных скважинах в полулогарифмических координатах (р, lnt) на основе зависимости (4.23), записанной относительно забоя скважины в виде

(4.32)

где

Уравнение (4.32) можно рассматривать как уравнение изменения забойного давления после остановки скважины, работающей до этого с постоянным дебитом Q.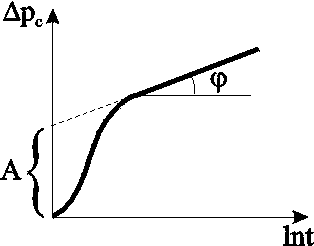




Рис. 4.8. Кривая КВД
Уравнение (4.32) представляет собой прямую (рис. 4.8) в координатах р_с–lnt, а коэффициент iопределяется как тангенс угла её наклона  к оси времени и коэффициент А – как отрезок оси давления, отсекаемый продолжением прямой.

По известным коэффициентам можно определить коллекторские свойства пласта:

• 
  по коэффициенту i определяют гидропроводность пласта
  

. (4.33)

• 
  Если известна вязкость жидкости в пластовых условиях  и толщина пласта h, то из последней формулы находится коэффициент проницаемости пласта:
  

. (4.34)

• 
  По известному угловому коэффициенту i = tg и радиусу r_c скважины из коэффициента А можно определить коэффициент пьезопроводности пласта æ.
  

Область применения указанных приемов интерпретации результатов исследования нефтяных скважин ограничивается условиями, при которых справедлива формула (4.32), а именно: скважина рассматривается как сток постоянной интенсивности в бесконечном, однородном пласте , и возможна мгновенная остановка притока флюида в скважину.

В случае ограниченного пласта, когда изменение давления, вызванное закрытием скважины, доходит до его границы, КВД начинает искажаться, а через достаточно большое время выходит на горизонтальную асимптоту, соответствующую стационарному распределению давления. Поэтому длина прямолинейного участка на кривой КВД ограничена.

Кроме того, в реальных условиях скважину нельзя остановить мгновенно. После её закрытия на устье приток флюида из пласта продолжается ещё некоторое время из-за упругости жидкостей и газов, заполняющих скважину. Время выхода на асимптоту должно, очевидно, превышать время дополнительного притока. Поэтому возможны условия, при которых прямолинейный участок на КВД появляется через значительный промежуток времени, либо даже вообще отсутствует.

На форму КВД сказывается также несовершенство скважины и возможное нарушение закона Дарси у стенок скважины.
4.2. Неустановившаяся фильтрация газа в пористой среде
4.2.1. Уравнение Лейбензона
Лейбензон Л.С. получил дифференциальное уравнение для определения давления в пласте при неустановившемся движении в нем идеального газа.

Для получения требуемого уравнения используем изотермическое приближение и, следовательно, используем уравнение состояния в виде

. (4.35)

Потенциальная функция, как уже отмечалось ранее, имеет вид

. (4.36)

Обозначив р²=Р и проделав преобразования общего уравнения нестационарной фильтрации, получим уравнение Лейбензона:

. (4.37)

По внешнему виду уравнение (4.37) не отличается от уравнения пьезопроводности (4.11), но множитель перед лапласианом переменен. В связи с этим уравнение (4.37) нелинейно в отличие от линейного уравнения пьезопроводности упругой жидкости и аналитически решается приближенно.

Для получения приближенного решения используется метод линеаризации, а именно, переменное давление р заменяется на некоторое постоянное : Лейбензон предложил замену на р_к (начальное давление в пласте); Чарный – на р_ср=р_min+0,7(p_max-p_min), где p_max и p_min – максимальное и минимальное давление в пласте за расчетный период.

При указанных допущениях решение будет иметь такой же вид, что и в случае упругой жидкости, но при этом в данных решениях давлению р будет соответствовать Р=р², æ – æ^/= , – .

Таким образом, изменение давления при нестационарной фильтрации газа описывается соотношением

. (4.38)

При малых значениях r²/(4æ^/t) можно заменить интегрально-показательную функцию логарифмической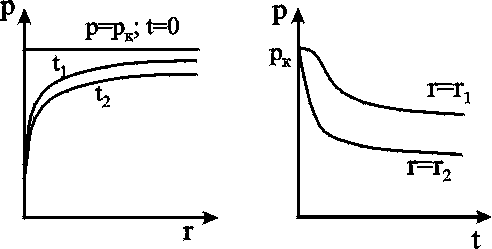

. (4.39)




a b

Рис. 4.9. Пьезометрические кривые при неустановившемся притоке газа к скважине в разные моменты времени (а) и изменение давления с течением времени в фиксированных точках пласта (b)
Формулы (4.38),(4.39) определяют при фиксированных значениях времени распределение давления вокруг газовой скважины, работающей с постоянным дебитом с момента t=0. Депрессионные кривые идентичны кривым при установившейся фильтрации – имеют максимальную кривизну вблизи скважины (рис.4.9а). Если задать значение r, то можно найти изменение давления в данной точке с течением времени (рис.4.9b). В частности, можно найти давление на забое (при r=r_c) после начала работы скважины.

Уравнение (4.39) используется для расчета коллекторских параметров газовых пластов методом обработки кривой восстановления давления. Принцип расчета такой же, что и в случае нефтяных скважин, но для получения линейной зависимости по оси ординат надо откладывать не депрессию, а разность квадратов пластового и забойного давлений.