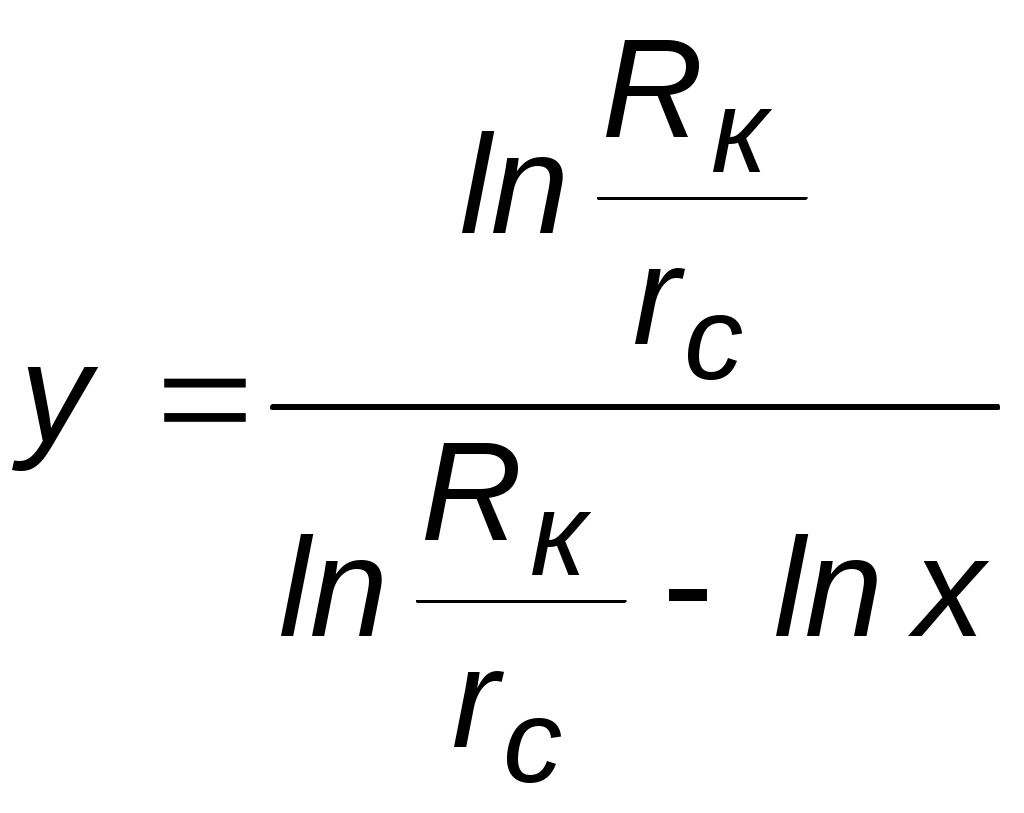Подземная гидромеханика
 Скачать 3.56 Mb. Скачать 3.56 Mb.
|
|
Идеальный газ в деформируемом (трещиноватом) пласте. Из (3.37) при подстановке выражений для плотности, проницаемости и приведённого к стандартным условиям объёмного дебита можно получить следующее выражение: 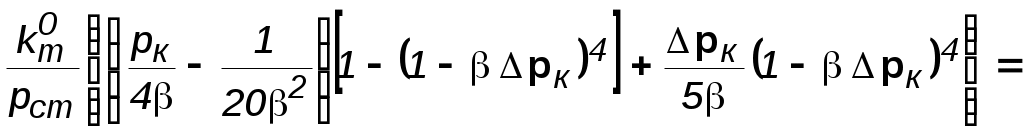 (3.38) (3.38)Зависимость величины проницаемости от метода обработки индикаторной диаграммы. В практике гидродинамических исследований скважин большое значение имеет этап идентификации индикаторных кривых, т.е. определение типов флюида и коллектора, а также закона притока флюида в скважину. Для примера рассмотрим, как изменение аппроксимации одних и тех же экспериментальных данных разными уравнениями притока приводит к значительному различию в значениях определяемой проницаемости (рис. 3.12).  а 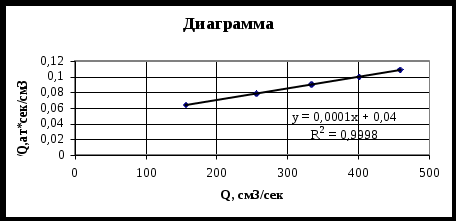 б Рис. 3.12. Аппроксимация индикаторной диаграммы различными уравнениями притока: .  Q=0,0972∆p – линейный закон фильтрации, без скин-эффекта; Q=0,0972∆p – линейный закон фильтрации, без скин-эффекта;. Q=0,132∆p -12,432 – линейный закон фильтрации, со скин-эффектом; . ∆p=0,0001Q2+0,04 Q – нелинейный закон фильтрации Из приведенных рисунков видно, что все аппроксимации находятся в области точности, удовлетворяющей точности, принятой при обработке гидродинамических исследований. В то же время, в первом случае мы имеем расчетную проницаемость k= 0,25 дарси, во втором – 0,19 дарси, а в третьем – 0,61 дарси. Таким образом, получаем, что по одним и тем же промысловым данным мы, если не сделать предварительно анализ вида течения, получим проницаемости пласта отличающие в несколько раз. Следовательно, и в прогнозируемой продуктивности пласта мы ошибемся в несколько раз. Если же, в результате мероприятий по интенсификации притока изменится тип коллектора, то, считая его неизменным, можно получить результаты ещё более отличающие. Отсюда следует, что применение даже очень совершенных расчетных методик может привести к неправильным результатам без предварительной оценки вида течения и коллектора, так как любая программа подбирает необходимое уравнение притока по заданной точности, а часто отличия могут крыться в области, принятой за достаточно точную. 3.3. Фильтрация в неоднородных средах В продуктивных пластах в различных точках проницаемость неодинакова. При мелкомасштабном хаотичном изменении фильтрационных характеристик по пласту пласт считается в среднем однородно–проницаемым. Пласт называется макронеоднородным, если его фильтрационные характеристики (проницаемость, пористость) значительно, скачкообразно отличаются в разных областях. Различают следующие виды макронеоднородности: а) Слоистая неоднородность (многослойный пласт), т.е. неоднородность по толщине пласта. Предполагается, что пропластки разделены непроницаемыми границами – гидравлически изолированы либо учитываются перетоки между слоями различной проницаемости – гидравлически сообщающиеся; поток в каждом пропластке – прямолинейно-параллельный или плоскорадиальный; в пределах каждого пропластка фильтрационные параметры постоянны, а на границе соседних они претерпевают скачок. Если течение потенциально, то полный дебит пласта определяется как сумма дебитов всех пропластков. При практических расчетах указанный многослойный пласт можно заменить квазиоднородным с эффективной проницаемостью где ki , hi – проницаемость и эффективная толщина i- го пропластка, h– эффективная толщина всего пласта. В случае слоистой неоднородности распределения давления по пропласткам идентично, а дебиты отличаются – наименьший дебит имеет пропласток минимальной проницаемости. б) Зональная неоднородность – пласт по площади состоит из нескольких зон различных фильтрационных параметров, на границах которых данные параметры меняются скачкообразно. Согласно уравнению неразрывности, массовый дебит постоянен и равен: при прямолинейно-параллельном потоке 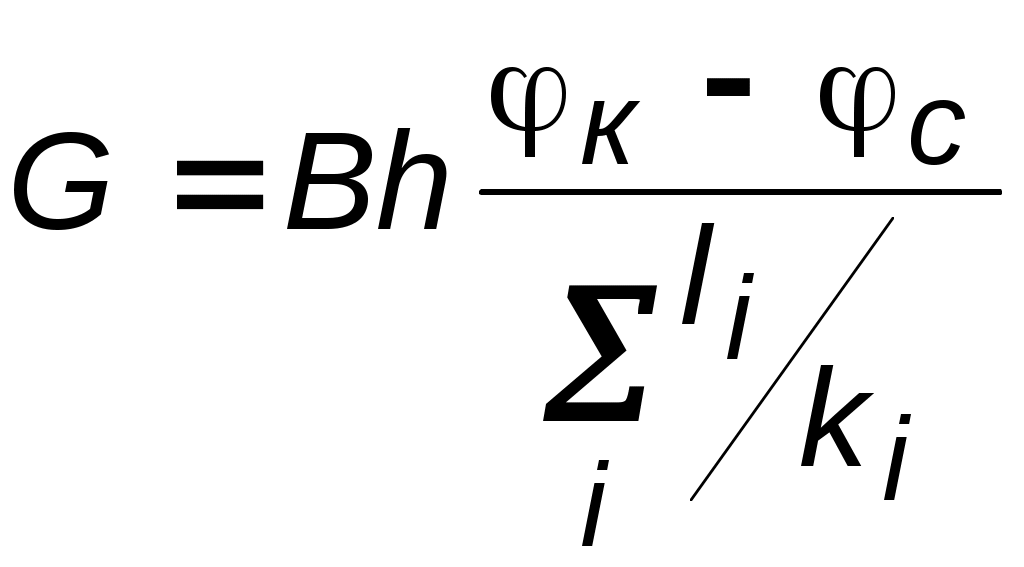 ; (3.40) ; (3.40)при плоскорадиальном потоке 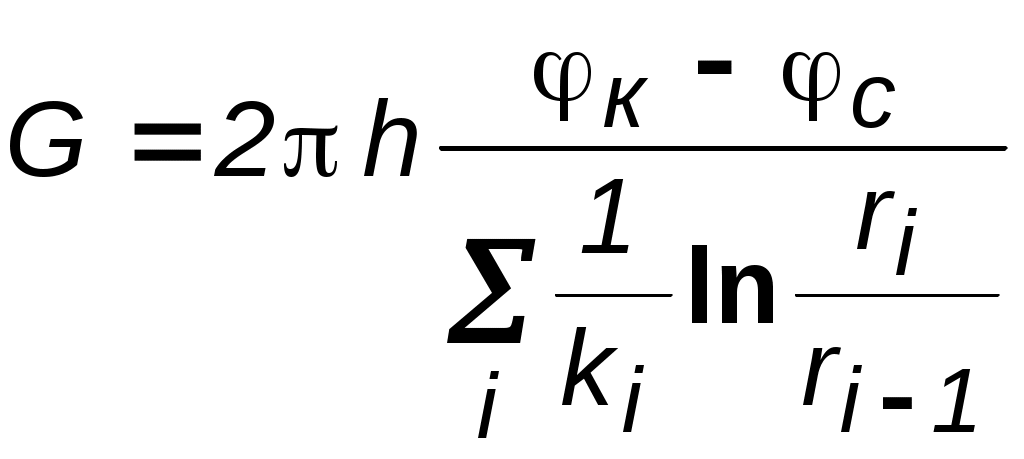 , (3.41) , (3.41)где li , ri – протяженность i - й зоны или её внешний радиус (r0=rc); В тоже время распределение давления представляет ломаную кривую с углом наклона обратно-пропорциональным проницаемости. При замене зонально-неоднородного пласта – квазиоднородным пластом следует использовать эффективные средние проницаемости: при прямолинейно–параллельном потоке 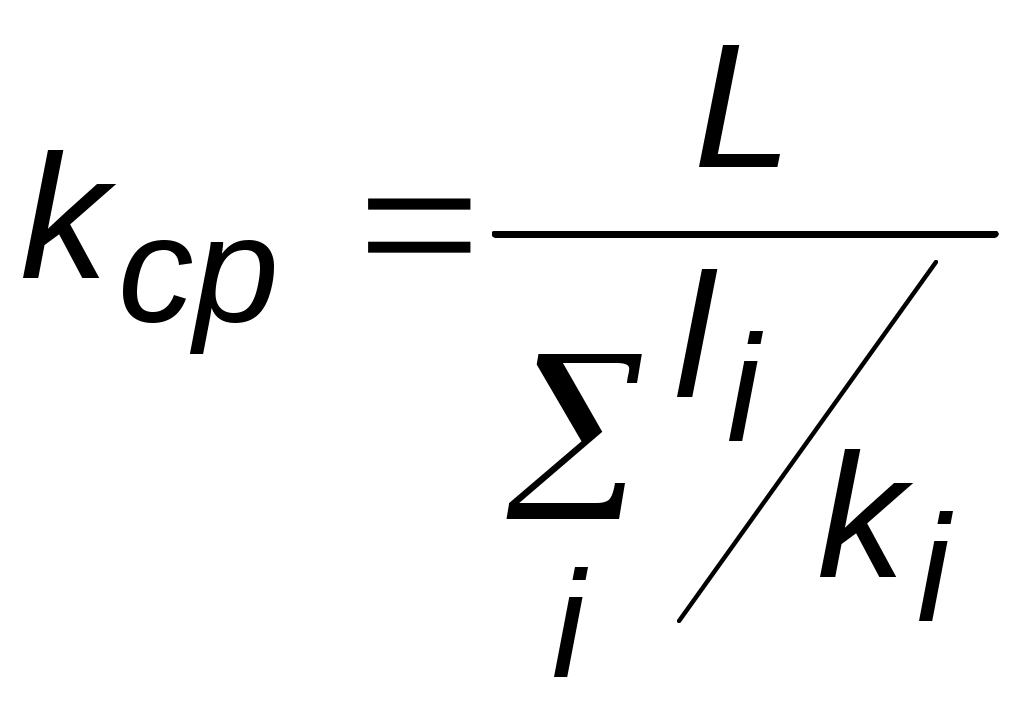 ; (3.42) ; (3.42)при плоскорадиальном потоке 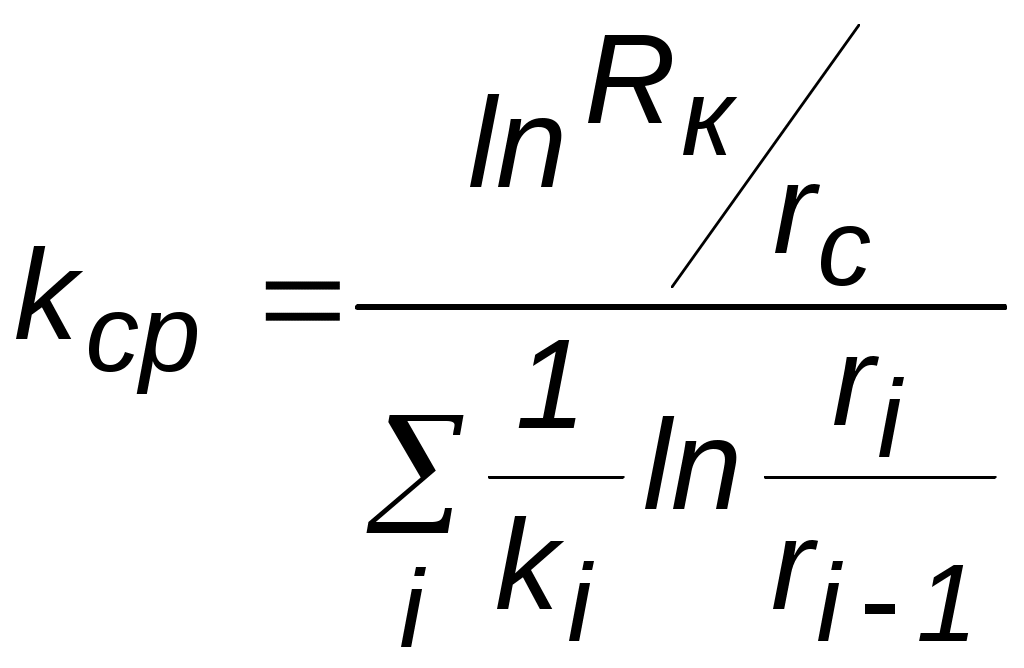 , (3.43) , (3.43)где L – расстояние от галереи до контура. В практике важен случай притока к скважине при наличии вокруг забоя кольцевой зоны с проницаемостью, отличной от проницаемости пласта (торпедирование или кислотная обработка, установка гравийного фильтра, глинизация или парафинизация призабойной зоны и т.д.). При данной задаче надо установить влияние различия проницаемостей кольцевой призабойной зоны и остальной части пласта на продуктивность скважины. С этой целью сравним дебит скважины в неоднородном пласте с двумя областями (n = 2 в формуле 3.41) проницаемости с дебитом скважины в однородном пласте (n = 1). Расчеты показывают: Недопустимость постановки прогноза на будущий дебит исходя только из данных о проницаемости призабойной зоны пласта, а следует использовать квазиоднородное приближение (формула 3.43). Ухудшение проницаемости призабойной зоны сильнее влияет на дебит, чем увеличение проницаемости в этой зоне. Если произойдёт заметное ухудшение проницаемости даже в небольшой области пласта, примыкающей к скважине, то дебит скважины резко снизится. В случае фильтрации по закону Дарси увеличивать проницаемость призабойной зоны более чем в 20 раз не имеет смысла, т.к. дальнейшее увеличение проницаемости практически не ведёт к росту дебита (при условии сохранения типа коллектора, например, в случае проведения кислотной обработки известняков образуются глубокие каналы растворения). Нарушение в пластовых условиях закона Дарси усиливает положительное влияние увеличенной проницаемости призабойной зоны на производительность скважины. 3.4. Приток к несовершенным скважинам 3.4.1. Виды и параметры несовершенств скважин Гидродинамическое несовершенство скважины проявляется в том, что в призабойной зоне пласта с конечной мощностью отсутствует радиальность потока по причине, обусловленной конструкцией забоя или фильтра. 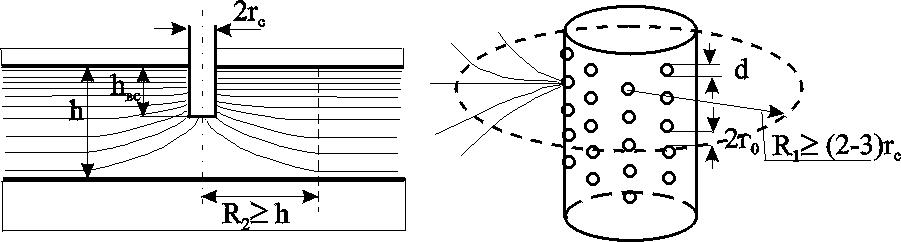 а b Рис. 3.12. Схема притока к несовершенной скважине: а – по степени вскрытия; b – по характеру вскрытия Различают два вида несовершенства скважин – несовершенство по степени вскрытия и несовершенство по характеру вскрытия. Несовершенная скважина по степени вскрытия – это скважина с открытым забоем, вскрывшая пласт не на всю мощность, а частично (рис.3.12,а). Скважина, хотя и доведённая до подошвы пласта, но сообщающаяся с пластом только через отверстия в колонне труб, в цементном кольце или в специальном фильтре, называется несовершенной по характеру вскрытия пласта (рис. 3.12,b). На практике чаще всего встречаются скважины несовершенные как по степени, так и по характеру вскрытия пласта. Дебит G несовершенной скважины обычно меньше дебита Gс совершенной, действующей в тех же условиях, что и данная несовершенная скважина. В некоторых случаях (при торпедной или кумулятивной перфорации, когда глубина прострела достаточно велика) может наблюдаться обратная картина. Отношение данных дебитов характеризует степень несовершенства скважины и называется параметром несовершенства Параметр несовершенства зависит от: относительного вскрытия пласта где hвс – глубина погружения скважины в пласт , h – толщина пласта; плотности перфорации (числа отверстий, приходящихся на 1м фильтра), размеров и формы отверстий; глубины прострела. При расчете несовершенных скважин нередко используют понятие приведенного радиуса несовершенной скважины где rC – радиус совершенной скважины, С – коэффициент несовершенства. Приведенный радиус – это радиус такой совершенной скважины, дебит которой равняется дебиту данной несовершенной скважины при тех же условиях эксплуатации. Таким образом, вначале находятся приведённые радиусы rпр и дальнейший расчет несовершенных скважин ведется как для совершенных скважин радиуса rпр. Таким образом, дебит несовершенной скважины можно определить, если известен параметр несовершенства или приведённый радиус rпр , а также известна соответствующая формула дебита совершенной скважины. Влияние несовершенства скважины на приток при существовании закона фильтрации Дарси можно учесть величиной коэффициента С, основываясь на электрической аналогии. Согласно данной аналогии различие в дебитах совершенной Gc и несовершенной G скважин объясняется наличием добавочного фильтрационного сопротивления несовершенной скважины величиной С/2h, т.е. дебит несовершенной скважины можно представить в виде: 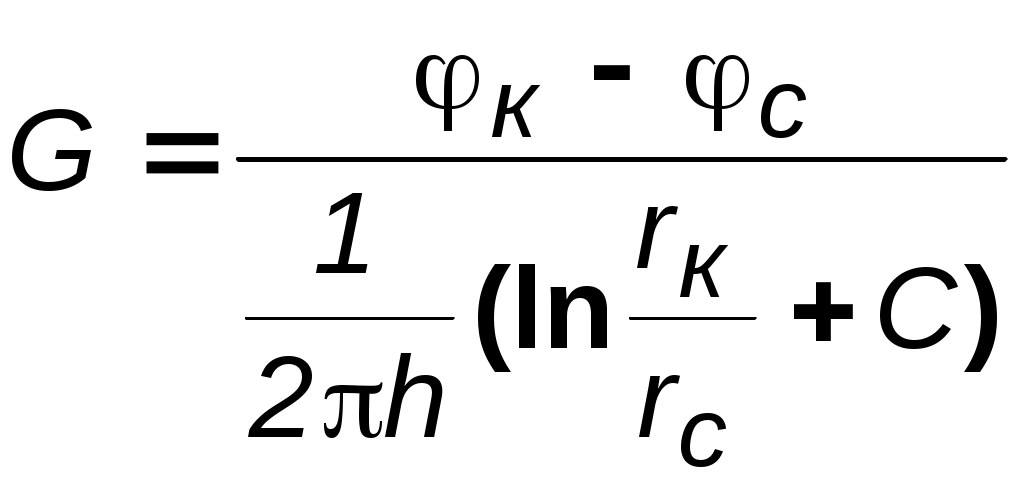 . (3.47) . (3.47)Учитывая (3.44), получаем зависимость между коэффициентом и и величиной С: 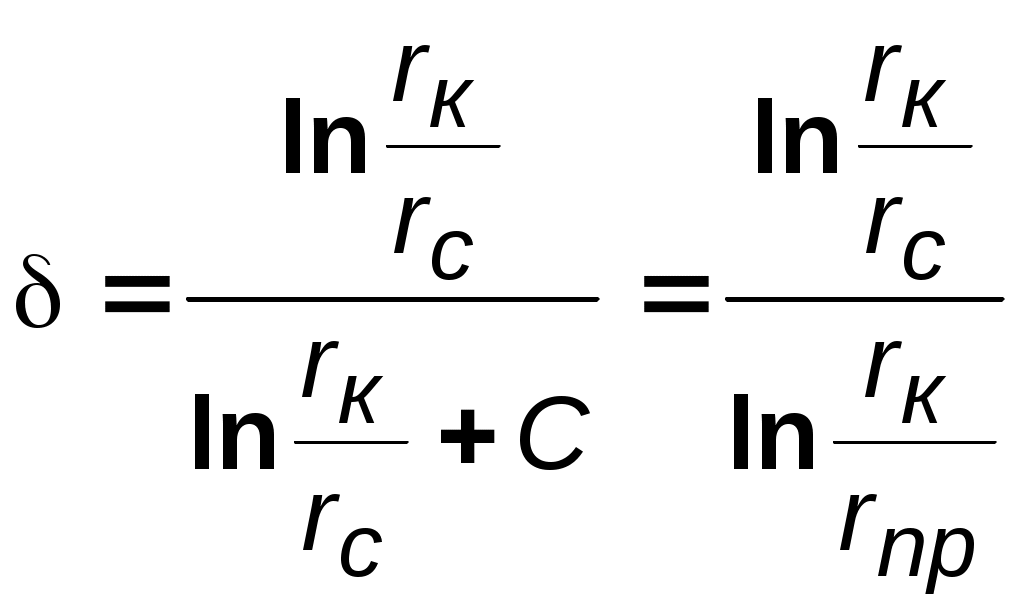 . (3.48) . (3.48)3.4.2. Исследования притока жидкости к несовершенной скважине Течение по закону Дарси. Несовершенная скважина по степени вскрытия изучалась В.И. Щуровым путём электролитического моделирования, который построил опытные диаграммы зависимости С от параметра a=h/D (h – мощность пласта, D – диаметр скважины) и относительного вскрытия пласта h=hвс/h. Таким же методом исследовалась несовершенная по характеру вскрытия скважина Щуровым и независимо от него И.М. Доуэллом и Маскетом, а также Р.А. Ховардом и М.С. Ватсоном. В результате получены зависимости коэффициента несовершенства от плотности перфорации (числа отверстий на 1 метр) и глубины прострела, которые показали значительную зависимость дебита от плотности перфорации только до значений 16–20 отверстий на 1 метр. Для случая фильтрации газа Е.М. Минским и П.П. Марковым доказана сильная нелинейная зависимость коэффициентов фильтрации от относительного вскрытия пласта. Для несовершенной по степени вскрытия на основе метода суперпозиции и отображения стоков Маскетом получена зависимость для дебита 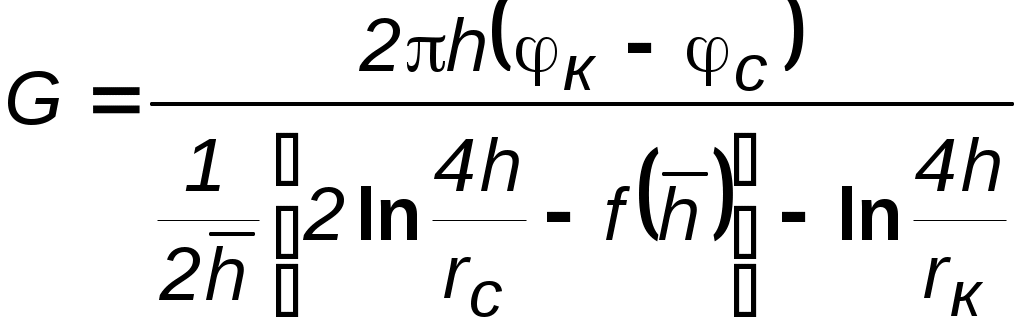 , (3.49) , (3.49)где f – функция относительного вскрытия (рис.3.12). 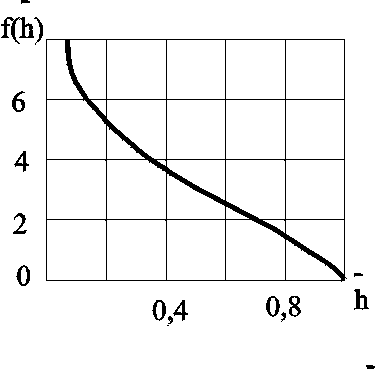 Рис. 3.12. График функции относительного вскрытия Если глубина вскрытия не слишком мала, то формула Маскета даёт хорошие результаты, а так как она проще остальных формул, то ею обычно и пользуются для скважин, несовершенных по степени вскрытия, но совершенных по характеру вскрытия. Если толщина пласта много больше радиуса скважины, то для расчета дебитов несовершенной по степени вскрытия скважины можно пользоваться более простой формулой Н.К.Гиринского: 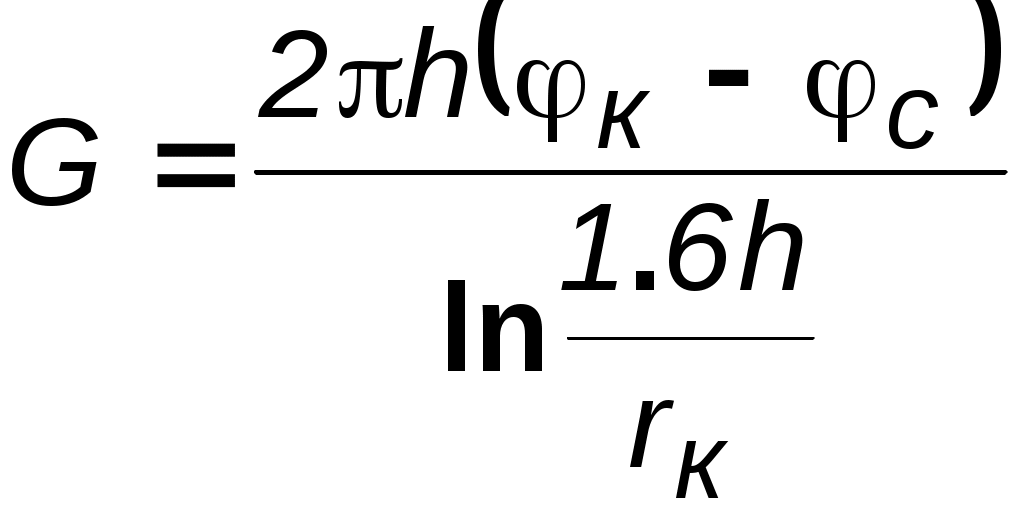 . (3.50) . (3.50)Из зависимости (3.49) видно, что коэффициент несовершенства по степени вскрытия С можно выразить соотношением: и он добавляется к фильтрационному сопротивлению совершенной скважины. Если скважины ещё и несовершенны по характеру вскрытия, то коэффициент С увеличивается на величину сопротивления фильтра где D – диаметр фильтрового отверстия в см; n – число отверстий на 1м перфорированной части. Течение реального газа по двухчленному закону. В большинстве случаев дебит газовых скважин не следует закону Дарси так же, как в некоторых случаях для нефтяных и водяных скважин. Вблизи фильтрационных отверстий при приближении к стенке скважины скорость фильтрации становится настолько большой, что число Рейнольдса превосходит критическое. Квадраты скоростей становятся настолько большими, что ими пренебрегать уже нельзя. Уравнение притока реального газа по двухчленному закону фильтрации к совершенной скважине записывается в виде, аналогично идеальному но здесь А и В являются функциями р и Т 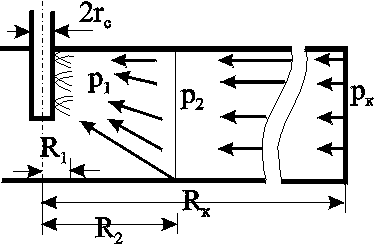 Рис.3.13. Схема притока к скважине несовершенной по степени и характеру вскрытия Приток к несовершенной скважине учитывается так же как и при фильтрации по закону Дарси, т.е. введением приведённого радиуса скважины При нарушении закона Дарси для скважины несовершенной по степени и характеру вскрытия для расчета притока проще всего использовать следующую схему. Круговой пласт делится на три области (рис. 3.13). Первая имеет радиус R1 (2–3) rc. Здесь из-за больших скоростей вблизи перфорации происходит нарушение закона Дарси и проявляется в основном несовершенство по характеру вскрытия. Вторая область – кольцевая с R1< r< R2 и R2h. Здесь линии тока искривляются из-за несовершенства по степени вскрытия, и фильтрация происходит тоже по двухчленному закону. В третьей области (R2< r< Rк) действует закон Дарси и течение плоскорадиально. Для третьей области Во второй области толщина пласта переменна и изменяется по линейному закону от hвс при r = R1 до h при r = R2 (hвс – глубина вскрытия), т.е. h(r) = r, где и определяются из условий h(r) = hвс при r = R1; h(r) = h при r = R2. Чтобы получить закон движения в этой области, надо проинтегрировать уравнение (3.31), предварительно подставив вместо постоянной толщины h переменную h(r) и учтя реальные свойства газа: где В первой области фильтрация происходит по двухчленному закону и плоскорадиальное течение нарушается из-за перфорационных отверстий. Уравнение притока имеет вид (3.56), но несовершенство учитывается коэффициентами С3 и С4, а R2 заменяется на R1 и R1 на rc. Коэффициент С3 определяется по графикам Щурова, а для определения С4 используется приближенная формула: где N – суммарное число отверстий; R0– глубина проникновения перфорационной пули в пласт. Складывая почленно (3.55), (3.56) и уравнение притока для первой области, получим уравнение притока для несовершенной скважины: где 3.5. Влияние радиуса скважины на её производительность Определим дебит в двух крайних случаях: по закону Дарси – первое слагаемое в формуле (3.33) и по закону Краснопольского развитого нелинейного течения – второе слагаемое. То же самое сделаем и в случае радиально–сферического течения. Если примем радиус одной скважины rс, а другой – rc/ = x.rc и, соответственно, дебиты G и G/, а их отношение обозначим через у = G/G/, то получим следующие формулы для вычисления предельных значений у. Из таблицы видно, что при сохранении закона Дарси в плоскорадиальном потоке влияние радиуса скважины на дебит невелико (необходимо увеличение радиуса в 10 раз, чтобы дебит вырос на 20%). Если же фильтрация нелинейна, то влияние rc на G усиливается. Для радиально-сферического потока дебит скважины зависит от радиуса в большей степени, особенно при нелинейном законе фильтрации. При торпедировании забоя, гидравлическом разрыве пласта и других способах воздействия на призабойную зону, образуются и расширяются трещины, что способствует нарушению закона Дарси и, следовательно, усилению влияния радиуса скважины на приток к ней жидкости.
| ||||||||||||