Подземная гидромеханика
 Скачать 3.56 Mb. Скачать 3.56 Mb.
|
3.1.1. Прямолинейно-параллельный поток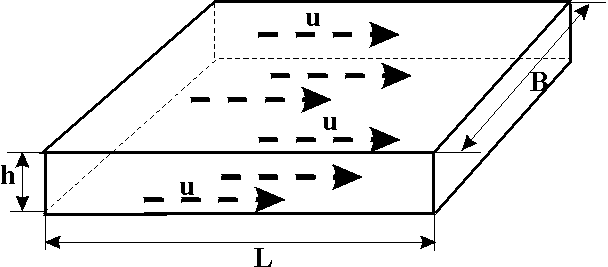 Рис. 3.1. Схема прямолинейно-параллельного течения Траектории всех частиц жидкости – параллельные прямые, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока равны между собой, поверхности равных потенциалов (эквипотенциальные поверхности) и поверхности равных скоростей (изотахи) являются плоскими поверхностями, перпендикулярными траекториям. Законы движения вдоль всех траекторий такого фильтрационного потока идентичны, а потому достаточно изучить движение вдоль одной из траекторий, которую можно принять за ось координат – ось х. Примеры а) Пласт (рис.3.1) имеет в плане полосообразную форму шириной B и длиной L, толщина пласта h постоянна, граничный контур непроницаем и непроницаемы кровля и подошва пласта. Батарея эксплуатационных скважин расположена параллельно начальному контуру нефтеносности. Приближение тем лучше, чем меньше расстояние между скважинами и если заменить батарею сплошной прямолинейной выработкой – галереей, то движение жидкости к галерее будет строго прямолинейно–параллельным. б) Поток между круговыми батареями нагнетательных и эксплуатационных скважин в случае больших радиусов батарей (угол схождения векторов скорости бесконечно мал). При этом толщина пласта постоянна, а его кровля и подошва непроницаемы. в) В лабораторных условиях при течении через цилиндрический керн или прямую трубу постоянного сечения, заполненную пористой или трещинной средой. 3.1.2. Плоскорадиальный поток 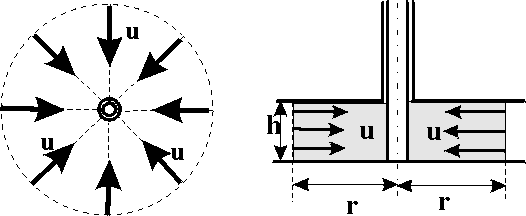 a b Рис. 3.2. Схема плоскорадиального течения: a – горизонтальное сечение; b –вертикальное сечение Траектории всех частиц жидкости – прямолинейные горизонтальные прямые, радиально сходящиеся к центру скважины, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока параллельны и равны между собой; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют цилиндрические окружности с осью, совпадающей с осью скважины. Схемы линий тока в любой горизонтальной плоскости потока будут идентичными и для характеристики потока достаточно рассмотреть движение жидкости в одной горизонтальной плоскости. Примеры а) Горизонтальный пласт постоянной толщины h и неограниченной протяженности, подошва и кровля пласта непроницаемы. Пласт вскрыт единственной гидродинамически совершенной скважиной (рис.3.2), то есть. вскрыт на всю толщину, и забой полностью открыт. Для эксплуатационной скважины поток – радиально-сходящийся, а для нагнетательной – радиально-расходящийся. Плоскорадиальным потоком будет занята вся зона от стенки скважины до контура питания. б) Гидродинамически несовершенная скважина (скважина с перфорированным забоем – несовершенство по характеру вскрытия или не полностью вскрывшая пласт – несовершенство по степени вскрытия). Вблизи скважины линии тока искривляются, и поток можно считать плоскорадиальным только при некотором удалении от скважины. в) Круговая батарея эксплуатационных скважин – поток плоскорадиален на некотором удалении, т.к. жидкость движется как бы к укрупнённой скважине радиуса, равного радиусу окружности батареи. 3.1.3. Радиально-сферический поток Траектории всех частиц жидкости – прямолинейные горизонтальные прямые, радиально сходящиеся к центру полусферического забоя; эквипотенциальные поверхности перпендикулярны траекториям и образуют сферические поверхности. Скорость фильтрации в любой точке потока является функцией только расстояния этой точки от центра забоя. Следовательно, этот вид фильтрационного потока также является одномерным. 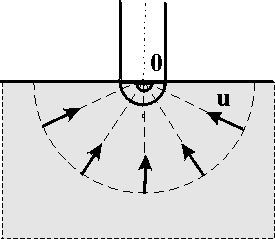 Рис. 3.3. Схема радиально-сферического течения Такой поток может реализовываться, когда скважина вскрывает только плоскую горизонтальную, непроницаемую кровлю пласта (рис.3.3). Пласт при этом должен быть неограниченной толщины, а забой иметь полусферическую форму. Приближение к данному виду потока тем лучше, чем глубина вскрытия меньше толщины пласта. Описанные три вида одномерного потока играют большую роль при решении многих задач нефтегазопромысловой практики. Естественно, моделируя реальное течение одним из трёх указанных видов, мы прибегаем к некоторой схематизации реальных пластов и течений жидкости. Тем не менее, рассмотренные схемы не только воспроизводят, хотя и приближенно простейшие случаи течения жидкости в реальном пласте, но и помогают изучать более сложные виды потоков пластовой жидкости в тех случаях, в которых сложный фильтрационный поток удобно представить себе состоящим из простейших видов потока. 3.2. Исследование одномерных течений 3.2.1. Задача исследования Задача исследования установившегося фильтрационного потока заключается в определении дебита (расхода), давления, градиента давления и скорости фильтрации в любой точке потока, а также в установлении закона движения частиц жидкости (или газа) вдоль их траекторий и в определении средневзвешенного по объёму порового пространства пластового давления. 3.2.2. Общее дифференциальное уравнение При условии вытеснения флюида из пласта или его нагнетания в пласт через галерею или скважину условимся принимать за координату произвольной точки пласта расстояние r до этой точки: от галереи (для прямолинейно- параллельного потока); от центра контура скважины в основной плоскости (плоскости подошвы пласта) фильтрации (для плоскорадиального потока); от центра полусферического забоя скважины (для сферически-радиального потока). В случае одномерного потока пласт представляется укрупнённой трубкой тока. Из условия неразрывности потока (уравнение 2.3) следует, что при установившейся одномерной фильтрации массовый расход G через все изобарические (эквипотенциальные) поверхности, определяемые уравнением r=const, в трубке тока будет один и тот же. Таким образом u= G /F( r ), (3.2) где F=F(r) – площадь эквипотенциальной поверхности в функции координаты r. Отметим, в данном случае средняя скорость фильтрации на некоторой эквипотенциальной поверхности совпадает со скоростью фильтрации в любой точке этой поверхности. Определим величину площади F для различных видов одномерных потоков: прямолинейно-параллельный поток – F( r ) =Bh; плоскорадиальный поток – F( r ) =2 h r; радиально-сферический поток – F( r ) = 2 r2. Обратившись к уравнению (2.7) следует отметить, что положительный массовый дебит будет в тех случаях, когда r отсчитывается от стока, то есть галерея или скважина – эксплуатационная. Приравнивая правые части (2.7) и (3.2), получаем общее дифференциальное уравнение трех простейших видов потенциального одномерного потока: где А и j имеют следующие значения: прямолинейно-параллельный поток – A = Bh, j = 0; плоскорадиальный поток – A = 2 h, j = 1; радиально-сферический поток – A = 2, j = 2. Параметр j получил название показателя формы потока, так как характеризует вид одномерного течения. Разделив в (3.3) переменные и проинтегрировав, получим: где С – произвольная постоянная, определяемая из граничных условий. Из формулы (3.4) следует, что она верна при значениях j=0;2. При j=1 (плоскорадиальный поток) интегрирование (3.3) даёт Найдем единственное решение, соответствующее заданным граничным условиям, т.е. определим постоянную С. Наиболее часто представляются следующие два варианта задачи: Известны постоянный массовый дебит G и значение потенциала на одной из граничных поверхностей рассматриваемой области пласта, например, на питающем контуре (пластовое значение потенциала) эксплуатационной галереи или скважины (G=G0 = const, = k при r=rk). Подставляя данные значения в (3.4), получаем: Для замыкания данного уравнения необходимо соотношение для массового дебита G = G0 = const. 2. Известны: значения потенциалов на двух граничных поверхностях пласта, например, на забое скважины и на границе пласта с областью питания (на контуре питания). Таким образом, = с при r = rc ; = k при r = rk . Подставляя в равенство (3.4) один раз значения rk и k, а другой раз значения с и rc, и исключая из двух полученных уравнений постоянную С, найдём массовый дебит G : 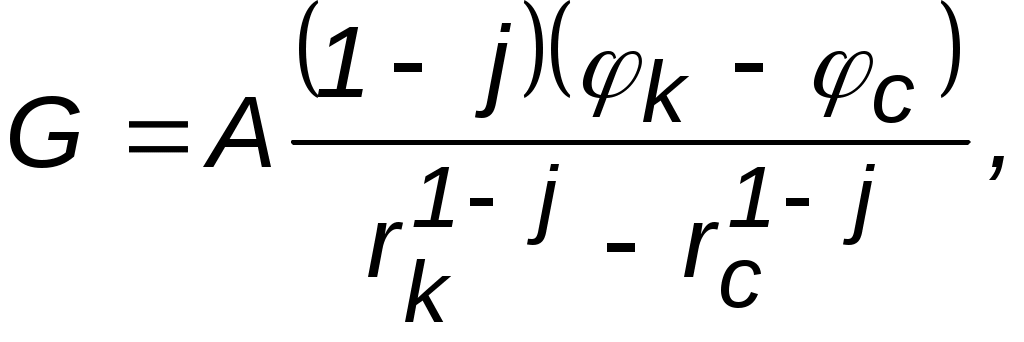 (3.7) (3.7)где значения А и j приведены выше. Исключая из (3.6) величину G/A, при помощи формулы (3.7) получаем: где По (3.8) можно определить значение потенциала для любой точки пласта с координатой r, если дебит неизвестен. В случае плоскорадиального потока (j = 1) соответственно рассмотренным выше двум вариантам задачи и поставленным граничным условиям получим равенства: 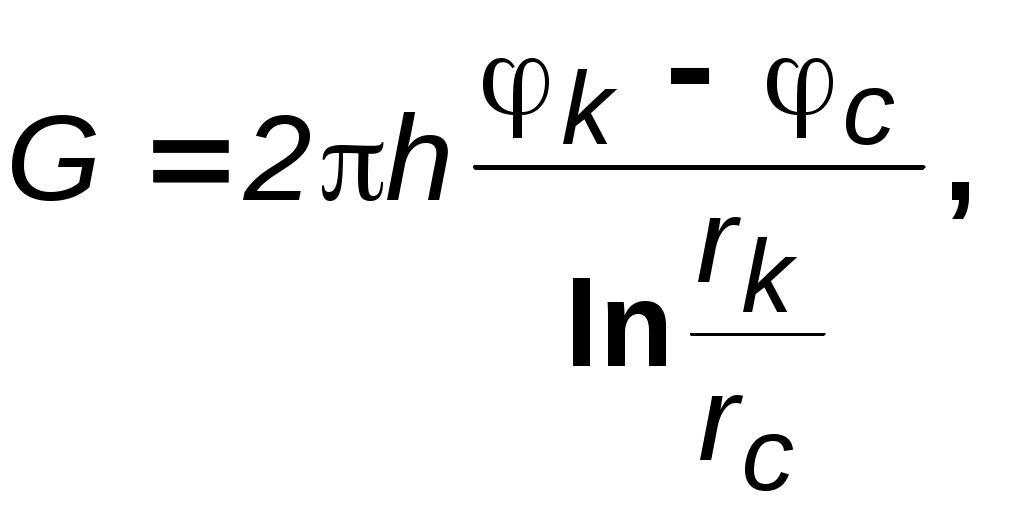 (3.9) (3.9)Таким образом, формулы (3.9), (3.10) действительны только для плоскорадиального потенциального потока любой жидкости. Для других видов одномерного движения имеем формулы (3.7), (3.8). Распределение градиента потенциала описывается зависимостью (3.3). 3.2.3. Потенциальные функции В предыдущем разделе были получены соотношения, определяющие распределения потенциала (3.8, 3.10) и градиента потенциала (3.3). В то же время потенциал величина абстрактная и не имеет физического смысла, а для практических задач исследования необходимо определение физических величин, таких как давление и скорость фильтрации. В связи с этим, определим выражения потенциальной функции (табл. 3.2) для случаев флюидов (табл.3.1) различной физической природы (жидкость или газ), а также различных типов коллекторов (пористые или трещинные). Таблица 3.1
|
