Подземная гидромеханика

• Название: Подземная гидромеханика
• Дата: 30.11.2022
• Размер: 3.56 Mb.
• Имя файла: Posobie_PGM.doc
• Тип: Учебное пособие; #820975
• страница: 8 из 17

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. 
   Какие потоки называются одномерными?
   
2. 
   Прямолинейно-параллельный поток. Примеры.
   
3. 
   Плоскорадиальный поток. Примеры.
   
4. 
   Радиально-сферический поток. Примеры.
   
5. 
   Что входит в исследование фильтрационного течения.
   
6. 
   Общее дифференциальное уравнение потенциального одномерного потока.
   
7. 
   Показатель формы потока.
   
8. 
   Получение выражения для потенциала и дебита плоскорадиального течения.
   
9. 
   Получение выражения для потенциала и дебита прямолинейно-параллельного и радиально-сферического течений.
   
10. 
    Потенциал несжимаемой жидкости в недеформируемом (пористом) пласте.
    
11. 
    Потенциал несжимаемой жидкости в деформируемом (трещинном) пласте.
    
12. 
    Потенциал упругой жидкости в недеформируемом пласте.
    
13. 
    Потенциал сжимаемой жидкости (газа) в недеформируемом (пористом) пласте.
    
14. 
    Уравнение Дюпюи.
    
15. 
    Коэффициент продуктивности. Размерность.
    
16. 
    Депрессия и воронка депрессии.
    
17. 
    Методика получения закона движения частиц жидкости.
    
18. 
    Методика вывода средневзвешенного давления.
    
19. 
    Индикаторная зависимость и индикаторная диаграмма.
    
20. 
    Нарисовать и объяснить графики давления, скорости фильтрации для несжимаемой жидкости в пористом и трещинном пластах.
    
21. 
    Нарисовать и объяснить графики давления, скорости фильтрации для несжимаемой жидкости и газа в пористом пласте.
    
22. 
    Нарисовать и объяснить индикаторные диаграммы для несжимаемой жидкости в пористом и трещинном пластах. В каких координатах надо строить диаграммы, чтобы получить прямолинейные зависимости.
    
23. 
    Нарисовать и объяснить индикаторные диаграммы для несжимаемой жидкости и газа в пористом пласте. В каких координатах надо строить диаграммы, чтобы получить прямолинейные зависимости.
    
24. 
    Соотношение дебитов реального и совершенного газов при одинаковых условиях.
    
25. 
    Принципиальное отличие зависимости для дебита упругой жидкости от несжимаемой.
    
26. 
    Отличие уравнений притока и дебита для несжимаемой жидкости, текущей по закону Дарси и по двухчленному закону.
    
27. 
    Зависимость величины проницаемости от метода обработки индикаторной диаграммы.
    
28. 
    Слоистая неоднородность. Зональная неоднородность.
    
29. 
    Эффективная проницаемость квазиоднородного пласта при слоистой неоднородности.
    
30. 
    Эффективная проницаемость прямолинейно-параллельного течения квазиоднородного пласта при зональной неоднородности.
    
31. 
    Эффективная проницаемость плоскорадиального течения квазиоднородного пласта при зональной неоднородности.
    
32. 
    Характер изменения дебита и давления в случаях слоистой и зональной неоднородностях.
    
33. 
    Характер влияния изменения проницаемости призабойной зоны на дебит в случае течения по закону Дарси и нелинейной фильтрации.
    
34. 
    Виды несовершенств скважины. Совершенная скважина.
    
35. 
    Приведенный радиус. Относительное вскрытие.
    
36. 
    Радиус зоны влияния несовершенств по степени и характеру вскрытия.
    
37. 
    Влияние радиуса скважины на её производительность при линейной и нелинейной фильтрации и различных типов одномерного течения.
    

4. НЕСТАЦИОНАРНАЯ ФИЛЬТРАЦИЯ УПРУГОЙ ЖИДКОСТИ И ГАЗА
4.1. Упругая жидкость
4.1.1. Понятия об упругом режиме пласта
При разработке нефтегазовых месторождений часто возникают неустановившиеся процессы, связанные с пуском или остановкой скважин, с изменением темпов отбора флюидов из скважин. Характер этих процессов проявляется в перераспределении пластового давления, в изменениях во времени скоростей фильтрации, дебитов скважин и т.д. Особенности данных процессов зависят от упругих свойств пластов и жидкостей, т.е. основная форма пластовой энергии данных упругих режимов – энергия упругой деформации жидкостей и материала пласта.

При упругом режиме движение возникает в призабойной зоне в начале эксплуатации скважины за счет использования потенциальной энергии упругой деформации пласта и жидкости и только через некоторое время оно распространяется на более отдалённые области.
При снижении пластового давления объём сжатой жидкости увеличивается, а объём порового пространства сокращается за счет расширения материала пласта. Всё это способствует вытеснению жидкости из пласта в скважину.

В ряде случаев приток жидкости поддерживается не только за счет упругих свойств пласта и жидкости, но и за счет напора воды, поступающей извне. Такой режим называется упруговодонапорным.

Если залежи нефти ограничены либо зонами выклинивания, либо экранами, то режим называется замкнутоупругим. Если вытеснение жидкости из пласта происходит не под действием преобладающего влияния упругости пласта и жидкости, то упруговодонапорный режим переходит в жестководонапорный режим. При этом режиме влияние упругости пласта и жидкости на фильтрационный поток хотя и не прекращается, но заметно не проявляется.

Неустановившиеся процессы протекают тем быстрее, чем больше коэффициент проницаемости пласта k, и тем медленнее, чем больше вязкость жидкости  и коэффициенты объёмной упругости жидкости и пласта.

4.1.2. Основные параметры теории упругого режима
Важнейшими параметрами теории упругого режима являются коэффициенты объёмной упругости жидкости и пласта.

Коэффициент объёмной упругости жидкости _f характеризует податливость жидкости изменению её объёма и показывает, на какую часть первоначального объёма изменяется объём жидкости при изменении давления на единицу

, (4.1)

где V_f – объём жидкости; знак минус указывает на то, что объём V_f увеличивается с уменьшением давления; _f нефти находится в пределах (7–30)10^-10м²/н; _f воды находится в пределах (2,7–5)10^-10 м²/н.

Коэффициент объёмной упругости пласта определяется по формуле

, (4.2)

где V_п – объём пласта; _С для слабо и сильно сцементированных горных пород находится в пределах (0,3–2)10^-10 м²/н.

Большое значение в практике добычи нефти и подсчета её запасов имеет величина упругого запаса выделенной области пласта, соответствующая заданному падению давления. По Щелкачеву упругий запас – это количество жидкости, высвобождающейся в процессе отбора из некоторой области пласта при снижении пластового давления до заданной величины, если высвобождение происходит за счет объёмного расширения жидкости и уменьшения порового пространства пласта.

Обозначая упругий запас через _{з ,} получаем по определению

_з = _fV_0fр + _с V_п р, (4.3)

где V_0f – объём жидкости, насыщающей элемент объёма пласта V_п при начальном давлении р₀; р – изменение давления.

Так как V_0f = m₀ V_п, то

_з=^* V_п р. (4.4)

Здесь ^* = m₀_ж +_с – коэффициент упругоёмкости пласта, показывающий долю объема жидкости от выделенного элемента объема пласта, высвобождающейся из элемента пласта при снижении давления на единицу.

Вскрытие пласта и изменение режима работы скважины вызывает возмущение в пласте. От источника возмущения оно передаётся во все стороны пласта с какой - то скоростью. Скорость распространения изменения пластового давления характеризуется коэффициентом пьезопроводности пласта

. (4.5)

Здесь L, T –размерности длины и времени.

В коллекторах – 1000см²/с  æ 50000см²/c или 0.1м²/с  æ 5м²/c.

Степень нестационарности процессов определяется безразмерными параметрами Фурье:

• 
  для призабойной зоны  (4.6)
  
• 
  для всего пласта – (4.7)
  

4.1.3. Уравнение пьезопроводности
Считаем, что течение происходит по закону Дарси. Для вывода уравнения пьезопроводности используем линеаризованное уравнение состояния упругой жидкости

, (4.8)

и соотношение, описывающее изменение пористости в зависимости от давления,

. (4.9)

Из (4.8) и (4.9), при пренебрежении членом, содержащим произведение _ж_с,имеем следующее дифференциальное уравнение

. (4.10)

В то же время из общего уравнения фильтрации (2.8) .

Подставляя в выражение для потенциала соотношение для плотности (4.8) и считая μ=const, k=const, после интегрирования данного выражения при пренебрежении членом, содержащим (р-р₀)², получим с учетом (2.8)
. (4.11)

Уравнение вида (4.11) известно под названием уравнения теплопроводности, а в теории фильтрации называется уравнением пьезопроводности. По аналогии с уравнением теплопроводности коэффициент æ характеризует быстроту изменения давления в пласте и называется коэффициентом пьезопроводности. Само уравнение (4.11) позволяет определить поле давления при нестационарных процессах в пласте с упругим режимом.
4.1.4. Приток к скважине в пласте неограниченных размеров
Вывод основного уравнения упругого режима. Считаем пласт упругим, горизонтальным и большой протяженности и в нём имеется одна скважина, тогда движение жидкости в пласте можно считать плоскорадиальным к точечному стоку (эксплуатационная скважина) или от точечного источника (нагнетательная скважина).

Рассмотрим процесс перераспределения давления при неустановившемся, плоском радиальном движении жидкости. Для этого запишем уравнение пьезопроводности в цилиндрической системе координат

. (4.12)

Предположим, что возмущение вызвано мгновенным стоком, существовавшим в момент t = t^/ . Для этого случая решение уравнения (4.12) имеет вид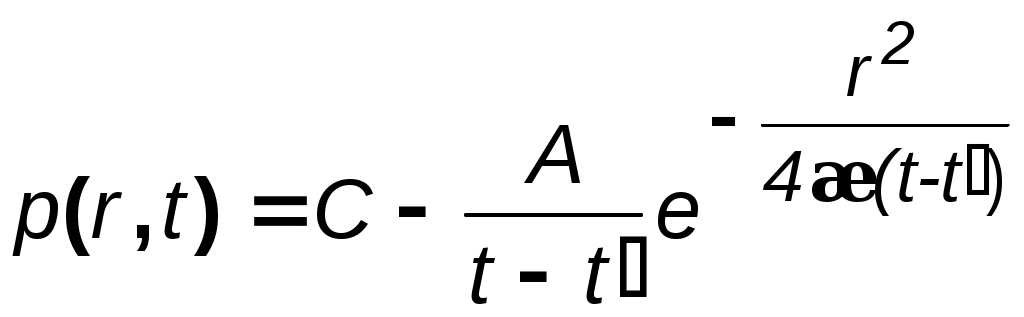

, (4.13)

где А и С – некоторые постоянные.

Найдём значения постоянных. Для этого будем считать, что в момент времени t = t^/ давление в пласте было р = р_к = const. Тогда при r> 0 и при t = t^/ второй член правой части обращается в неопределённость типа 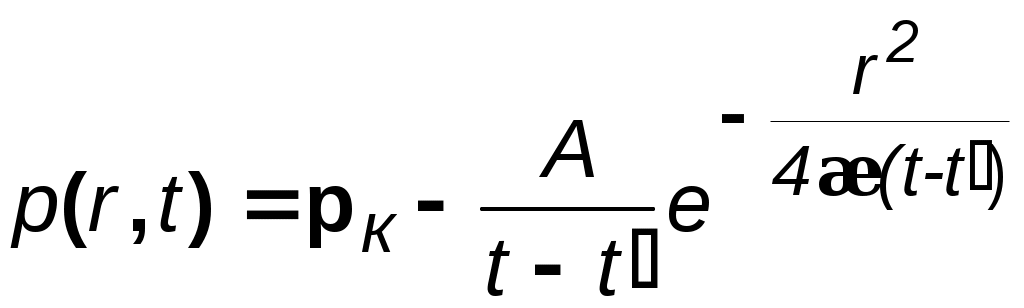/ и определяется по правилу Лопиталя, что даёт С = р_к. Таким образом,

. (4.14)

Для определения коэффициента А воспользуемся соотношением (4.4) для случая кольцевого элемента пласта с внутренним радиусом r, толщиной h и шириной dr, а также учтем падение давления р = p₀ - p по (4.14):

d_з = ^*рd V_п = 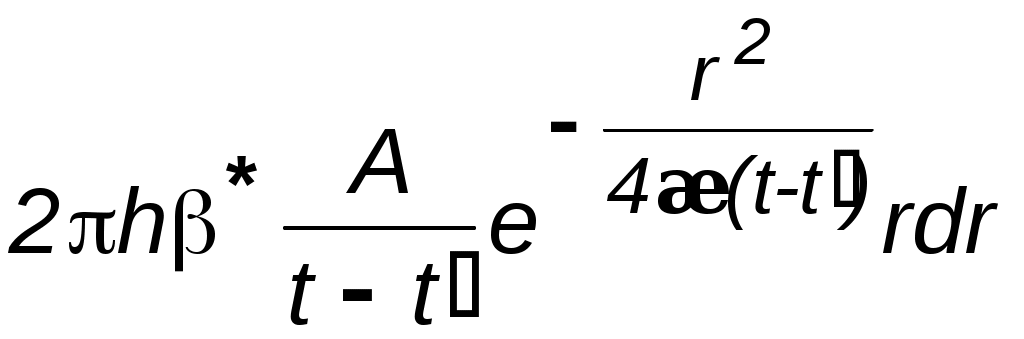. (4.15)

После интегрирования (4.15) в пределах от 0 до  получим объём жидкости ₃ , выделившейся из всего пласта и, учитывая выражение для , определим коэффициент А:

. (4.16)

Таким образом в случае скважины, введенной в неограниченный пласт в некоторый (начальный) момент времени и действующей мгновенно, изменение давления во времени определяется соотношением: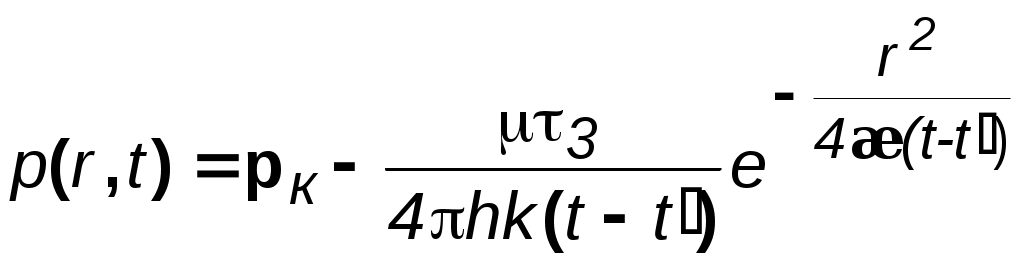

. (4.17)

Если скважина была введена в некоторый момент времени и действовала непрерывно с постоянным дебитом Q = Q₀ в течение времени dt^/, то за этот промежуток времени через сток выделяется из пласта объём d_з = Qdt и, следовательно, из (4.17) следует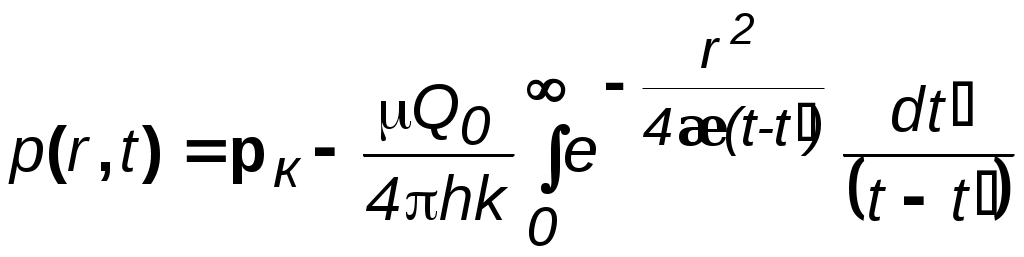

. (4.18)

Интеграл правой части носит название интегрально-показательной функции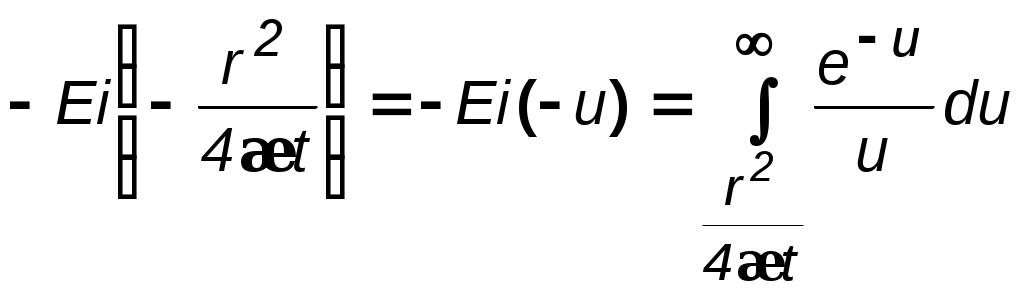



и с учетом данного обозначения решение для изменения давления запишется в виде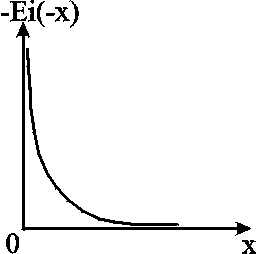

. (4.19)





Рис. 4.1. График интегрально-показательной функции
Формула (4.19) является основной формулой теории упругого режима пласта.
Интегрально-показательная функция имеет вид (рис.4.1) и обладает следующими свойствами:

• 
  -Ei(-u) изменяется от 0 до  при изменении аргумента от 0 до ;
  
• 
  функция -Ei(-u) представляется в виде сходящегося ряда
  

(4.20)

Для малых значений u<1 можно принять

(4.21)

с погрешностью, не превышающей 0,25% при u<0,01; 5,7% – при u<0,1

. (4.22)

С учетом соотношения (4.21) основное уравнение (4.19) перепишется в виде, которое более известно под названием уравнение кривой восстановления давления (КВД)

. (4.23)

Полученную зависимость можно использовать при числе Фурье 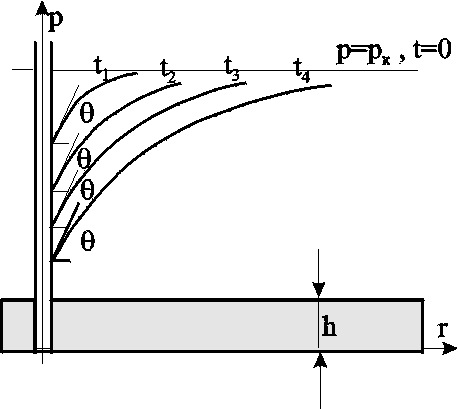с погрешностью, не превышающей 0,6%. Практически это означает, что уже через 1 с после пуска скважины расчеты забойного давления, выполненные по формуле (4.23), будут иметь погрешность не превышающую 0,6%. Формулу (4.23) можно использовать и для расчета падения давления в конечном пласте, а именно, погрешность расчета давления при этом не превышает 1%, если r_к > 1000rc и fo < 3,4.105 или Fo < 0,34.



Рис. 4.2. Пьезометрические кривые при пуске скважины в бесконечном пласте с постоянным дебитом

Рассмотрим пьезометрические кривые для бесконечного пласта, который эксплуатируется скважиной радиуса r_c c постоянным дебитом Q₀(рис. 4.2). Для точек вблизи забоя можно пользоваться формулой (4.23), а дифференцируя её по координате r, найдём градиент давления

.

Из этой формулы следует, что градиент давления для значений r, удовлетворяющих неравенству r²<<0,03.4 æ t, практически не зависит от времени и определяется по той же формуле, что для установившейся плоскорадиальной фильтрации несжимаемой жидкости. Для указанных значений r пьезометрические кривые представляют собой логарифмические линии (рис.4.2). Углы наклона касательных на забое скважины одинаковы для всех кривых.