Подземная гидромеханика
 Скачать 3.56 Mb. Скачать 3.56 Mb.
|
|
\Уравнения неразрывности. первой фазы второй фазы Если вытесняемая и вытесняющая фазы – слабосжимаемые упругие жидкости, то влиянием сжимаемости на распределение насыщенности можно пренебречь, так как время перераспределения давления за счет сжимаемости жидкостей, по крайней мере, на два порядка меньше, чем время вытеснения. Отсюда следует, что нестационарные процессы упругого перераспределения давления заканчиваются в начале процесса вытеснения. В некоторых случаях можно считать несжимаемым и газ в пластовых условиях. Если жидкости и пористую среду можно предполагать несжимаемыми, то уравнения (5.7) и (5.8) упрощаются Уравнения движения для многофазной фильтрации. При записи закона фильтрации предполагаем, что в любой точке каждая из фаз находится в термодинамическо - равновесном состоянии. Тогда для течения двухфазной смеси можно ввести в рассмотрение относительные проницаемости ki() и капиллярное давление рк (), зависящее только от насыщенности. Кроме этого, рассматриваем только однонаправленные процессы фильтрации, не учитывая гистерезисных явлений. Тогда выполняется закон фильтрации (5.4): а связь между давлениями в фазах определяется равенствами (5.5) и (5.6): Для замыкания полученной системы уравнений необходимо задать дополнительные соотношения, рассмотренные в разделе 1 и связывающие параметры фаз и пористой среды с давлением. Постановка и решение задач на основе полной системы уравнений фильтрации неоднородных жидкостей затруднительны ввиду сложности самих уравнений, а также формулировки краевых условий, в частности, разрыва капиллярных сил на границах пористой среды (так называемых концевых эффектов), роль которых недостаточно изучена. Анализ одномерных двухфазных потоков позволяет выявить основные эффекты и характерные особенности совместной фильтрации жидкостей. 5.4. Потенциальное движение газированной жидкости Газированная жидкость представляет собой смесь жидкой и газовой фаз. Газ находится не только в свободном состоянии; часть его растворена в жидком компоненте смеси. В пластовой нефти обычно содержится природный газ. Если давление в пласте выше давления насыщения нефти газом, то весь газ растворяется в нефти, а нефть называется недонасыщенной. Задача об одномерном потоке такой нефти относится к ранее описанным гомогенным задачам. Если же пластовое давление ниже давления насыщения, то в процессе движения нефти в пласте из нее выделяется газ и образуется движущаяся смесь нефти и свободного газа – газированная нефть. По мере продвижения смеси в направлении снижения давления из капельно - жидкого раствора (жидкого компонента смеси) выделяется все новая масса газа. Выделяющийся из раствора газ присоединяется к движущемуся свободному газу, вследствие чего увеличивается часть порового пространства, занимаемого газом. Свободный газ становится все более подвижным и фазовая проницаемость породы для газа растет, а фазовая проницаемость для жидкой фазы уменьшается. Вследствие этого расчеты параметров такого газо-жидкостного потока проводят на основе многофазной модели течения. Так общее дифференциальное уравнение одномерных потоков (3.3) можно применительно к капельно-жидкой фазе газированной жидкости записать следующим образом где Массовый дебит газового компонента смеси Gг находится как сумма массового дебита газа, движущегося в свободном состоянии Gгс, и массового дебита газа, движущегося в растворенном состоянии Gгр. Используя формулу (3.3) для свободного газа смеси, получим: где Для газа, находящегося в растворе, найдем где σм(р) = Gгр/Gf – массовая растворимость газа в жидкости, т. е. количество массы газа, растворенное в единице массы жидкости при давлении р. Суммируя почленно равенства (5.13) и (5.14), получим: Для газированной жидкости пользуются при расчетах величиной объемного газового фактора Г, который представляет собой отношение объемного газового дебита Qг, приведенного к стандартным условиям, к объемному дебиту жидкого компонента Qж, приведенному к тем же условиям. Поскольку массовый дебит на всех изобарических поверхностях в данном одномерном установившемся потоке один и тот же, сохраняется постоянным вдоль всего потока и газовый фактор Г. Учитывая, что где объемная растворимость газа в жидкости Если газ однороден, то в широких пределах (примерно от 1 до 100 ат) объемная растворимость пропорциональна давлению, т. е. σ(р) =р, (5.17) где – объемный козффиииент растворимости, постоянный для данных жидкости и газа. Формула (5.17) выражает закон Генри растворимости газа в жидкости. В соотношении для газового фактора (5.16) определим функции г(р) и f(р) в соответствии с формулой В практических расчетах по технологии нефтедобычи учитывается величина объемного коэффициента нефти, зависящего от давления р. Объемный коэффициент нефти (р) характеризует изменение объема нефти вследствие изменений давления и количества растворенного газа. Величина (р) есть отношение удельных объемов нефти в пластовых и атмосферных условиях. Согласно данному определению Заменяя в формуле (5.18) отношение 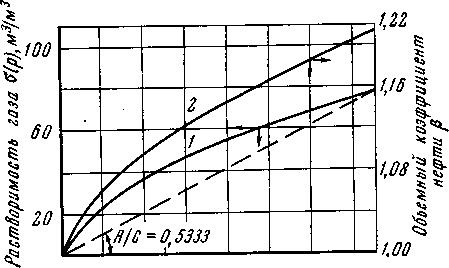 Рис. 5.4 Кривые зависимости коэффициента растворимости газа в нефти и объёмного коэффициента нефти от давления При постоянном газовом факторе Гуравнение (5.19), выражая зависимость между давлением р и насыщенностью s, служит уравнением состояния газированной жидкости. Функции μf(р), μг(p), (р) и σ(р)определяются по экспериментальным данным. На рис. 5.4 представлены зависимости растворимости σ(р) и объемного коэффициента нефти (р) от давления р. Потенциальная функция для газированной жидкости имеет вид где i=f, г; k*i(s) = ki/k, смотря по тому, движение какой фазы изучается – жидкой или газовой. Потенциальную функцию (р) можно определить путем численного интегрирования. Расчетные формулы для дебита по закону Дарси имеют наиболее простой вид, когда жидкость однородна и несжимаема. Такова, например, формула Дюпюи для объемного дебита Q. Придадим формуле для объемного дебита жидкой фазы газированной смеси в плоскорадиальном потоке вид формулы Дюпюи, сохранив в ней неизменным множитель рк - рс. Пусть k, f и μf – постоянны. Тогда из (5.20): где Ф (рк) и Ф (pc) – граничные значения интеграла вида Вычитая почленно равенства (5.21) и применяя известную теорему о среднем в интегральном исчислении, получим: 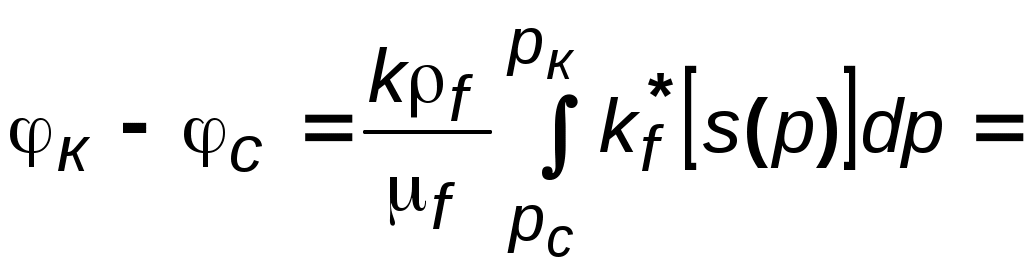 , (5.22) , (5.22)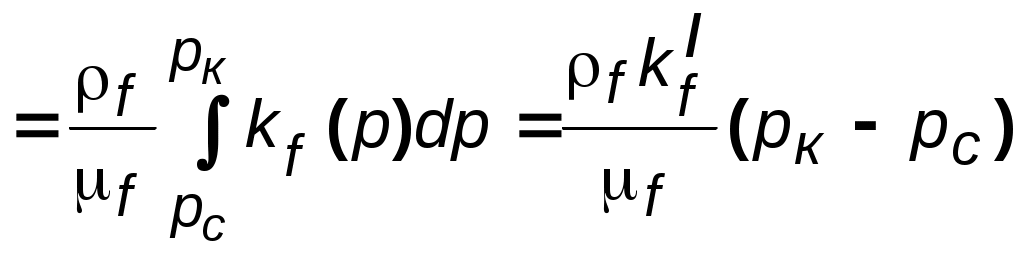 где k'f – некоторое среднее значение функции kf(р) в интервале изменения р от рс до рк. 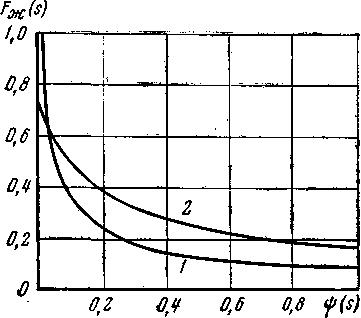 Подставляя полученное значение к-с в формулу (3.9) и разделяя на постоянное f, найдем, что: Подставляя полученное значение к-с в формулу (3.9) и разделяя на постоянное f, найдем, что: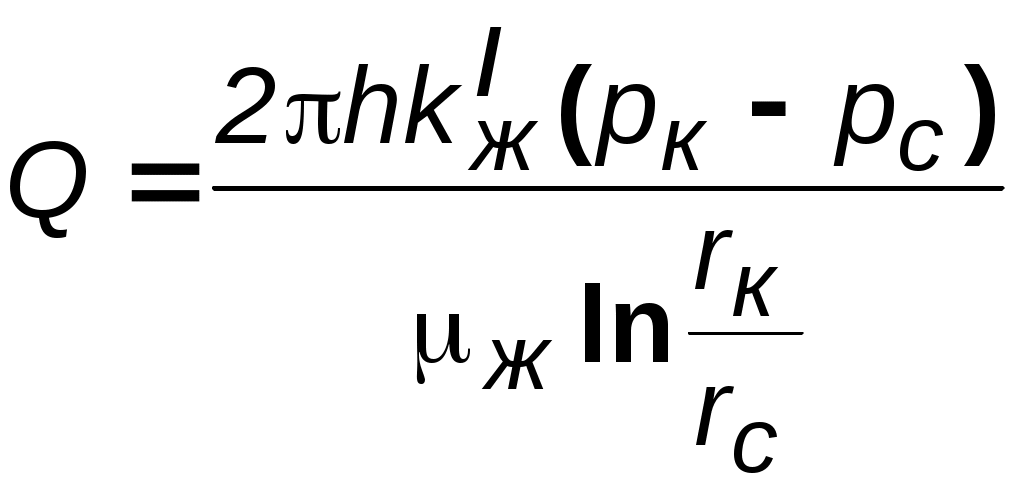 . (5.23) . (5.23)Имеем явное сходство с формулой Дюпюи.  Рис.5.5. Зависимость между относительной проницаемостью для жидкости и функцией (s) 1– сцементированные пески; 2 – несцементированные пески Таким образом, при расчете дебита жидкого компонента газированной жидкости можно использовать формулы для определения Gили Qдля однородной несжимаемой жидкости, если заменить в них проницаемость пласта kнекоторым средним значением фазовой проницаемости kf. Другими словами – определить дебит газированной жидкости можно, заменив газированную жидкость воображаемой однородной несжимаемой жидкостью, движущейся в пласте с коэффициентом проницаемости k'f, меньшим k. Среднее значение проницаемости k'f определяется с помощью формулы (5.19), по которой вычисляется (s), соответствующее некоторому среднему давлению рср. Это давление можно принять равным среднему арифметическому от рк и рс при небольшом изменении по пласту насыщенности s. Взяв вычисленное (s), находим k'f по графику на рис. 5.5. Хотя формулы Дюпюи и (5.23) сходны между собой, это сходство чисто внешнее и они отличаются по физическому содержанию. В действительности при движении однородной несжимаемой жидкости в пласте с проницаемостью k мы на основании формулы Дюпюи можем утверждать, что дебит пропорционален депрессии рс = рк - рс, независимо от величины давления рк или рс. Для газированной жидкости дебит зависит не только от депрессии рс, но и от величины давления рк или рс. В этом легко убедиться, если вспомнить, что средняя фазовая проницаемость k'f обусловлена значениями граничных давлений рк и рс. Следует отметить, что в действительности величина средней фазовой проницаемости зависит от целого ряда параметров для жидкости, газа и пласта. Некоторые выводы 1. Дебит газированной жидкости при прочих равных условиях всегда меньше дебита однородной несжимаемой жидкости. С повышением газового фактора при неизменяющейся депрессии рс дебит жидкой фазы уменьшается, а дебит газа увеличивается; при этом показатель ε растет, хотя и непропорционально G. 2. При данной депрессии рс и газовом факторе Г более высокий дебит будет при более высоком пластовом давлении. Это объясняется тем, что при более высоких давлениях меньшее количество пластового газа находится в свободном состоянии, чем при более низких давлениях. Следовательно, повышается фазовая проницаемость жидкости. Так как для обеспечения притока нефти к забою скважин необходимо создание депрессии р = рк - рс, причем с ростом депрессии дебит скважин увеличивается, то для повышения добычи более эффективным средством является увеличение депрессии за счет повышения пластового (контурного) давления рк, но не путем снижения забойного давления рс. Отмеченный факт подчеркивает большое значение своевременно принятых мер по поддержанию или повышению пластового давления в первых же стадиях разработки нефтяных месторождений. 3. Зависимость дебита жидкости и газа от депрессии, в отличие от однородной жидкости, не является линейной, хотя фильтрация каждой из фаз газированной жидкости принимается следующей линейному закону фильтрации. Таким образом, искривление индикаторной линии при фильтрации газированной жидкости еще не означает наличия отклонений от линейного закона фильтрации. Индикаторная кривая для реальной газированной нефти имеет меньший наклон, чем кривая для идеальной газированной жидкости. Это указывает на то, что для реальной жидкости существуют добавочные сопротивления при фильтрации, не учтенные в идеальной жидкости. 4. Рассмотрение нестационарной фильтрации газированной жидкости показывает, что начальный период (первые месяцы) неустановившейся радиальной фильтрации газированной жидкости в условиях режима растворенного газа характеризуется высокими дебитами жидкости и газа. Величина дебита жидкости быстро уменьшается с течением времени. Темп падения дебита газа меньше, чем темп падения дебита жидкости. В дальнейшем темп падения дебита жидкости резко уменьшается и наступает период относительно стабильной добычи, но абсолютная величина дебита жидкости невелика (уменьшается на порядок). Темп падения дебита газа в этот период времени уменьшается гораздо медленнее, чем темп падения дебита жидкости. Газовый фактор сначала резко возрастает, достигая в скором времени максимума, затем постепенно уменьшается. 5.5. Фильтрация водонефтяной смеси и многофазной жидкости Искусственное заводнение нефтеносных пластов, осуществляемое нагнетанием воды в пласт, приводит к необходимости изучать движение смеси воды и нефти в пласте. Движения водонефтяной смеси в пласте наблюдается также при наличии в пласте природной воды. Сюда относится связанная (реликтовая) вода; подошвенная вода, занимающая нижнюю часть пласта; краевая или контурная вода, первоначально располагающаяся за контуром нефтеносности и в последующем вытесняющая нефть к скважинам. Породы, из которых сложены продуктивные пласты, могут быть нефтесмачиваемыми (гидрофобными) и водосмачиваемыми (гидрофильными). Наиболее распространены водосмачиваемые породы; в них реликтовая вода как бы прилипает к стенкам поровых каналов. Высокая насыщенность реликтовой водой и служит вероятным признаком водосмачиваемости пород, тогда как нефтесмачиваемость проявляется в низкой насыщенности реликтовой водой. Отделение той или иной жидкости (нефти, воды) в сетке поровых каналов обусловлено насыщенностью и характеристикой смачиваемости. 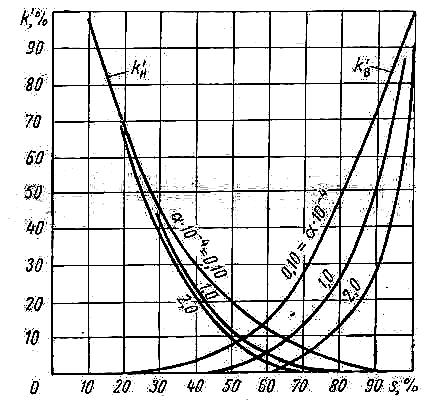 Рис. 5.6. Зависимость относительных фазовых проницаемостей для нефти и воды от водонасыщенности s при разных значениях параметра (по Леверетту) Результатом опытов Леверетта явились кривые, представленные на рис. 5.6. По оси абсцисс отложены значения водонасыщенности sв процентах, по оси ординат – относительная фазовая проницаемость для воды и нефти в процентах. Каждая кривая отвечает определенному значению параметра = ΔL/dΔp, где – давление вытеснения в см рт. ст., ΔL – длина колонки песка в см, d – средний диаметр поровых каналов в см и Δp –перепад давления в см рт. ст. Параметр пропорционален капиллярным силам, противодействующим прохождению отдельных капель нефти через поры песка. Для одномерного потенциального движения несжимаемой водонефтяной массы без учета массовых сил и фазовых превращений справедливо равенство Здесь kв и kн – фазовые проницаемости воды и нефти, соответственно; μв и μн – коэффициенты вязкости воды и нефти. Расчеты, относящиеся к одномерному потоку смеси воды и нефти, выполняются по ранее рассмотренным формулам однородной жидкости. При движении газированной жидкости в пластах содержатся обычно три фазы компонента смеси: нефть, газ и вода. В таком случае имеем поток многофазной жидкости. На основании экспериментов можно считать, что относительная фазовая проницаемость в многофазном потоке почти не зависит от вязкости жидкости, ее плотности, внутрижидкостного натяжения, градиента давления и пористости среды. В то время как вязкость существенно не влияет на относительную проницаемость, отношение величин вязкости жидких фаз, присутствующих одновременно в потоке, значительно влияет на состав текущей смеси. 5.6. Одномерные модели вытеснения несмешивающихся жидкостей Наиболее разработана в настоящее время теория одномерного движения двухфазной жидкости в пористой среде. Основные допущения этой теории состоят в следующем: жидкости предполагаются несмешивающимися (взаимно нерастворимыми); жидкости считаются несжимаемыми, а пористая среда – недеформируемой; фазовые переходы отсутствуют; коэффициенты вязкости фаз постоянны; относительные фазовые проницаемости и капиллярное давление являются известными однозначными функциями насыщенности; гистерезисные явления не учитываются (рассматриваются только однонаправленные процессы). 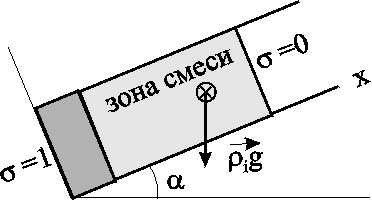 Рис. 5.7. Схема одномерной двухфазной фильтрации с учетом силы тяжести Полная система уравнений. Основываясь на этих допущениях, выведем полную систему уравнений двухфазной фильтрации в однородной пористой среде с учетом капиллярных и гравитационных сил. В случае прямолинейно-параллельного течения вдоль оси х (рис.5.7) уравнения неразрывности (5.9) для фаз принимают вид Обобщенный закон Дарси (5.10) сводится к уравнениям Здесь – угол наклона оси х к горизонту (рис. 5.8); 1 и 2 – плотности фаз. Неизвестные характеристики течения , u1, u2, p1 и p2 зависят от координаты х и времени t. Уравнения (5.25), (5.26) с учетом дополнительных соотношений образуют замкнутую систему для случаев линейного течения, являющуюся основой для решения задач вытеснения одной жидкости другой. Характерной особенностью данной системы является то, что её можно свести к одному уравнению для насыщенности. Знание распределения насыщенности в пласте позволяет проанализировать эффективность вытеснения нефти или газа несмешивающейся с ними жидкостью. где u=u1+u2; =2-1; функция Баклея–Леверетта или функция распределения потоков фаз Уравнение (5.27) представляет собой сложное нелинейное уравнение параболического типа второго порядка и точное решение получено лишь для некоторых сравнительно простых частных случаев. Начальные и граничные условия. При решении конкретных задач для уравнения изменения насыщенности должны быть сформулированы соответствующие граничные и начальные условия. В качестве начального условия задаются значения неизвестной функции в зависимости от пространственных координат при t = 0. Можно считать, что при t = 0 насыщенность всюду постоянна (например, = *). В случае вытеснения нефти водой естественно задать на входе в пласт (нагнетательная скважина или галерея) расход закачиваемой воды и равенство нулю скорости фильтрации нефти; из последнего условия вытекает, что k2 = 0, следовательно, на этой поверхности = *. На выходе из пласта возможно два варианта граничных условий. 1. Можно пренебречь градиентом капиллярного давления по сравнению с градиентом давления в фазах, т. е. считать, что 2. Экспериментально установлено, что вода не вытекает из гидрофильного пласта, а накапливается в выходном сечении, пока её насыщенность не достигнет значения *. В момент достижения значения * вода прорывается из пласта с сохранением на выходе этого значения насыщенности. Это явление получило название концевого эффекта. Математически оно приводится к сложному нелинейному граничному условию на выходе. Дифференциальное уравнение второго порядка для насыщенности (5.27) можно упростить путем учета только одного вида сил (гравитационных или капиллярных) и получить, соответственно, две различные модели: Модель Рапопорта Лиса. Для прямолинейно-параллельного вытеснения уравнение для насыщенности без учета силы тяжести было впервые получено в 1953 г. американскими исследователями Л. Рапопортом и В. Лисом. Поэтому модели двухфазной фильтрации с учетом капиллярных эффектов называют обычно моделями Рапопорта–Лиса. Дифференциальное уравнение для насыщенности в данной модели – параболического типа. |
