Подземная гидромеханика
 Скачать 3.56 Mb.
|
|
Модель Баклея Леверетта. Без учета капиллярных сил двухфазная фильтрация для случая прямолинейно-параллельного вытеснения рассматривалась С. Баклеем и М. Левереттом в 1942 г., а позже независимо от них А. М. Пирвердяном, исследовавшим также случай более общего закона фильтрации при двухфазном течении. Задачи двухфазной фильтрации без учета капиллярных сил известны как задачи (модель) Баклея – Леверетта. Задачи вытеснения такого типа в одномерной постановке изучены достаточно полно. Уравнение насыщенности задач данного типа принадлежит к классу квазилинейных гиперболических уравнений первого порядка. 5.6.1. Задача Баклея Леверетта и ее обобщения В случае одномерного течения несжимаемых несмешивающихся жидкостей в условиях, когда можно пренебречь капиллярным давлением процесс вытеснения допускает простое математическое описание. Для обоих случаев одномерного потока (прямолинейно-параллельного и плоскорадиального) это приводит к классической в теории вытеснения модели Баклея Леверетта. 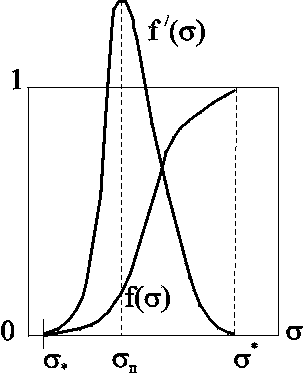 Рис. 5.8. Вид функции Баклея–Леверетта и её производной В рассматриваемом случае важное значение имеет так называемая функция Баклея Леверетта или функция распределения потоков фаз f(), которая имеет простой физический смысл. Действительно, данная функция представляет собой отношение скорости фильтрации вытесняющей фазы к суммарной скорости, и равна объемной доле потока вытесняющей жидкости (воды) в суммарном потоке двух фаз. Таким образом, функция Баклея – Лаверетта определяет полноту вытеснения и характер распределения нефтегазоконденсатонасыщенности по пласту. Задачи повышения нефте- и газоконденсатоотдачи в значительной степени сводятся к применению таких воздействий на пласт, которые в конечном счете изменяют вид функции f() в направлении увеличения полноты вытеснения. 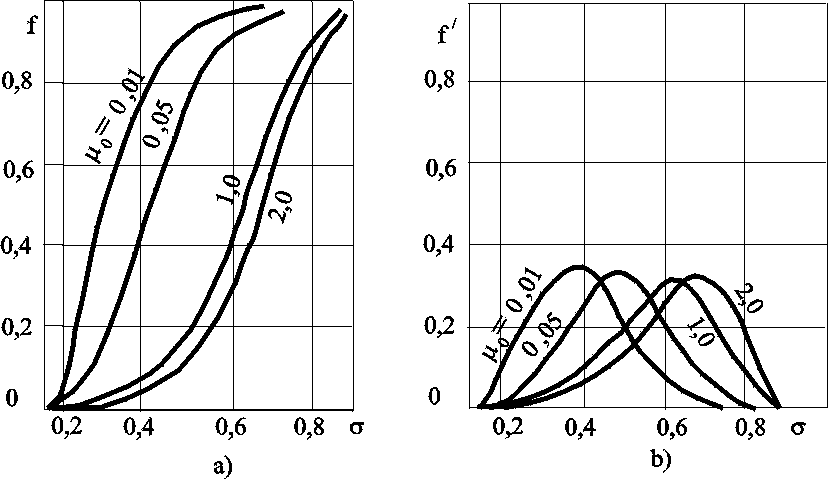 Рис. 5.9. Графики функции Баклея–Леверетта (а) и её производной (b) для различных отношений вязкости 0 Вид кривых функции f() и ее производной f/() показан на рис.5.8. С ростом насыщенности f() монотонно возрастает от 0 до 1. Характерной особенностью графика f() является наличие точки перегиба п , участков вогнутости и выпуклости, где вторая производная f//(), соответственно, больше и меньше нуля. Эта особенность в большой степени определяет специфику фильтрационных задач вытеснения в рамках модели Баклея – Леверетта. Зависимость функций f() и f/() от отношения вязкостей фаз 0=1/ 2 показана рис. 5.9. Из данного рисунка следует, что с ростом отношения вязкостей кривая f() сдвигается вправо и эффективность вытеснения возрастает. Например, применение пен и загустителей, повышающих вязкость нагнетаемой воды, может значительно увеличить нефтеотдачу. 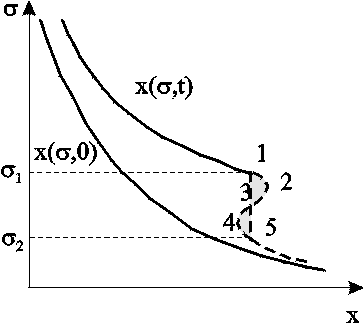 Рис. 5.10. Устранение многозначности распределения насыщенности введением скачка Физической особенностью модели двухфазного вытеснения Баклея – Леверетта является зависимость скорости распространения насыщенности от её величины. Это явление называется дисперсией волн. При 0 п большие насыщенности распространяются с большими скоростями, а при п 1 скорость распространения постоянного значения насыщенности начинает уменьшаться. Последнее приводит к тому, что, начиная с некоторого момента времени, распределение насыщенности оказывается многозначным (рис.5.10, кривая 1–2–3–4–5). В области данного участка одному и тому же значению х соответствуют три значения насыщенности : 1, 2 и 3, что физически невозможно, так как в каждом сечении пласта в любой момент времени может существовать только одна насыщенность. Данная неоднозначность устраняется введением скачка насыщенности (рис.5.11, отрезок 1–3–5). Скорость распространения скачка при этом равна скорости распространения насыщенности. Необходимо отметить, что в действительности математический скачок насыщенности не имеет места. Он появляется в решении вследствие пренебрежения капиллярными силами, за счет которых появляется некоторая “переходная зона” вблизи фронта вытеснения, в которой насыщенность изменяется непрерывно. В общем случае неодномерного вытеснения, а также при учете сжимаемости одной из фаз рассмотренная задача уже не сводится к одному уравнению для насыщенности. Необходимо совместно определять давление и насыщенность. Численные решения таких задач могут быть получены лишь на ЭВМ. 5.6.2. Задача Рапопорта – Лиса Учет капиллярного скачка давления рк, который задается в виде известной эмпирической функции насыщенностей, приводит к теории следующего приближения – модели Рапопорта – Лиса. При этом пренебрегаем силой тяжести. Действие капиллярных сил проявляется в основном вблизи фронта вытеснения, где градиенты насыщенности велики. Эти силы приводят к “размазыванию” фронта, поэтому при учете капиллярных сил скачок насыщенности отсутствует и насыщенность изменяется непрерывно. 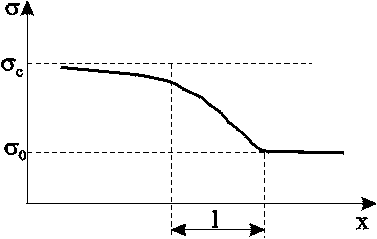 Рис. 5.11. Распределение насыщенности в стабилизированной зоне Тем не менее, экспериментально было обнаружено существование так называемой стабилизированной зоны насыщенности, которая перемещается, не изменяя своей формы, и распределение насыщенности в ней при постоянной скорости вытеснения – стационарно. В теории Баклея – Лаверетта (при пренебрежении капиллярными силами) стабилизированная зона моделируется скачком. Модель Рапопорта – Лиса позволяет определить ширину данной зоны l (рис. 5.11) и распределение насыщенностей по ней. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ Гомо- и гетерогенные системы. Насыщенность порового пространства i –й фазой. Скорость фильтрации i –й фазы. Закон Дарси для i –й фазы. Зависимость относительных проницаемостей от насыщенности. От каких параметров зависит относительная проницаемость? Что такое капиллярное давление и от каких параметров оно зависит? Почему сумма относительных проницаемостей меньше 1? Нарисуйте диаграмму для определения границ преобладания потоков различных фаз при трехфазном течении. Как зависит функция Леверетта от насыщенности в случае насыщения и пропитки? Уравнения неразрывности для двухфазного потока в случае сжимаемых и несжимаемых сред. От каких параметров зависит капиллярное давление? Что такое недонасыщенная нефть? Условия существования газированной нефти. Общее дифференциальное уравнение одномернного потока капельно-жидкой фазы, растворенного и свободного газа газированной жидкости. Массовая растворимость газа в жидкости. Объемный газовый фактор. Объемная растворимость газа в жидкости. Закон Генри растворимости газа в жидкости. Чему равно значение равномерной насыщенности? Объемный коэффициент нефти. Как зависит растворимость от давления? Определить дебит газированной жидкости по формулам гомогенной. Отличие формулы для определения дебита газированной жидкости от формулы Дюпюи по физическому содержанию. Взаимосвзь дебитов газированной и гомогенной жидкостей. Зависимость дебита газированной жидкости от величины пластового давления. Физическое объяснение. Отличие идикаторной диаграммы газированной жидкости от гомогенной. Особенности поведения дебитов и газового фактора для газированной жидкости во время пуска скважины. Классы пород по степени смачиваемости. Допущения теории одномерного движения двухфазной жидкости в пористой среде. Функция Баклея – Леверетта или функция распределения потоков фаз. Граничные условия для уравнения изменения насыщенности. Сущность концевого эффекта. Модель Рапопорта – Лиса. Модель Баклея – Леверетта. Вид функции Баклея –Леверетта и её производной. Физический смысл функции Баклея –Леверетта. Характер изменения функции Баклея –Леверетта в зависмости от изменения относительной вязкости. Дисперсия волн. Физическая природа скачка насыщенности. Стабилизированная зона насыщенности. 6.ОСНОВЫ ФИЛЬТРАЦИИ НЕНЬЮТОНОВСКИХ ЖИДКОСТЕЙ При очень малых перепадах течение жидкостей в пластах, как отмечалось ранее, не подчиняется закону Дарси и поведение жидкости аномально. Данная аномальность связана с физико–химическим взаимодействием фильтрующихся жидкостей с материалом пористой среды, а сами жидкости при этом получили название неньютоновские. Кроме этого, наличие нелинейной связи тензора скоростей деформации с тензором напряжения может проявляться и в ряде других случаев. Так повышенное содержание в нефтях высокомолекулярных компонентов (смол, асфальтенов, парафина) приводит к проявлению неньютоновских свойств флюидов при их фильтрации. Развитие методов воздействия на природные залежи с целью увеличения нефте- и газоконденсатоотдачи приводит к значительному расширению ассортимента веществ, закачиваемых в продуктивные пласты. Многие из этих веществ (высокомолекулярные соединения, полимеры) не обладают свойствами ньютоновских жидкостей. Поэтому рассмотрение особенностей фильтрации неньютоновских систем приобретает самостоятельное значение. Для простоты будем рассматривать нелинейные законы фильтрации, описывающие только безинерционные движения при условии, что фильтрующиеся жидкости обладают неньютоновскими свойствами. 6.1. Реологические модели фильтрующихся жидкостей и нелинейные законы фильтрации Течение ньютоновской жидкости описывается законом Ньютона:  , (6.1)где du/dy – градиент скорости в направлении перпендикулярном направлению течения х. Зависимость между и du/dy является в этом случае прямой линией, проходящей через начало координат (рис. 6.1, кривая 2). Жидкости, не подчиняющиеся закону трения (6.1), называются аномальными или неньютоновскими. Неньютоновские жидкости можно разбить на три класса: 1. Стационарно реологические жидкости – касательное напряжение зависит только от градиента скорости:  . (6.2)2. Нестационарно реологические жидкости – связь между и du/dy зависит от времени действия напряжений  . (6.3)3. Вязкоупругие жидкости – среды, обладающие свойствами как твердого тела, так и жидкости, а также способные к частичному восстановлению формы после снятия напряжений. Для таких сред зависимость между касательными напряжениями и градиентом скорости более сложная; она включает производные по времени как напряжений, так и градиента скорости Среди неньютоновских жидкостей первого класса, описываемых уравнением (6.2), можно выделить три типа: Вязкопластичные жидкости, для которых уравнение (6.2) имеет вид 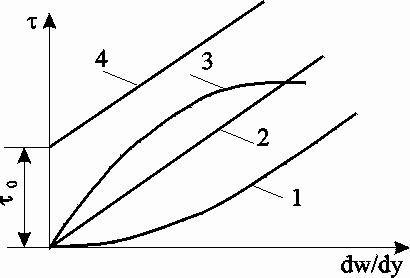 при >0 , (6.4) при 0 . Рис. 6.1. Зависимость касательного напряжения от градиента скорости: жидкость: 1 – дилатантная; 2 – ньютоновская; 3 – псевдопластичная; 4 – вязкопластичная Графическое представление этой зависимости, называемое реологической кривой, приведено на рис. 6.1 (кривая 4). В равенство (6.3), кроме коэффициента вязкости , входит также постоянная 0, называемая начальным (или предельным) напряжением сдвига. Считается, что при 0 жидкость ведет себя как твердое тело и течение отсутствует. Это объясняется наличием у покоящейся вязкопластичной жидкости пространственной жесткой структуры, сопротивляющейся любому напряжению , меньшему 0. Когда становится больше 0, структура разрушается. 2. Псевдопластичные жидкости. Эксперименты показали, что для ряда сред связь между напряжением сдвига и градиентом скорости в логарифмических координатах оказывается на некотором участке линейной с угловым коэффициентом от 0 до 1. Поэтому для описания таких сред используется степенная зависимость  , (n < 1), (6.5)где k и n постоянны для данной жидкости; коэффициент k – мера консистенции жидкости; отличие показателя n от единицы характеризует степень отклонения данной жидкости от ньютоновской. Типичная реологическая кривая (6.4) псевдопластичной жидкости приведена на рис. 6.1 (кривая 3). Модель псевдопластичной жидкости применяется, в частности, для описания движения растворов и расплавов полимеров. Указанные реологические соотношения можно привести к ньютоновскому виду путем введения понятия кажущейся вязкости *, как отношения касательного напряжения к градиенту скорости: 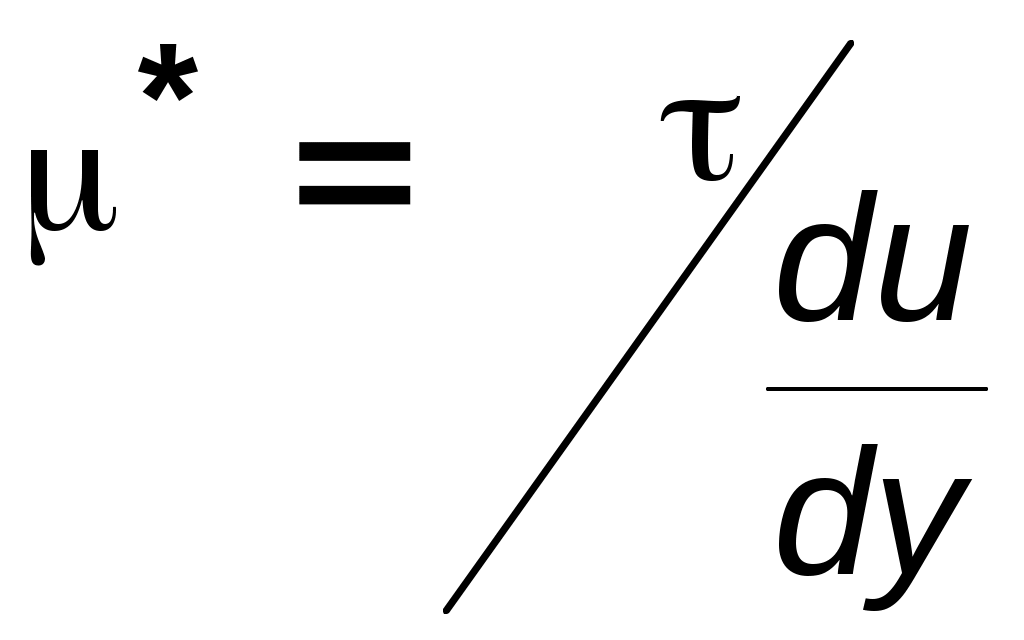 .Для псевдопластичной жидкости, как следует из (6.4), эта величина  и так как n<:1, то * убывает с возрастанием градиента скорости.3. Дилатантные жидкости описываются степенным уравнением (6.4), но при n>1. Кривая течения представлена на рис. 6.1 (кривая 1). У этих жидкостей кажущаяся вязкость * увеличивается с возрастанием градиента скорости. Модель дилатантной жидкости хорошо описывает свойства суспензий с большим содержанием твердой фазы. В зависимости от вида неньютоновской жидкости по-разному записывается и закон фильтрации. Так закон фильтрации вязкопластичной жидкости (6.3) в пористой среде записывается в виде:  u>0; (6.6) , u=0, где  – – предельный (начальный) градиент.В соответствии с (6.5) скорость фильтрации u отлична от нуля только в тех областях, где gradp> (рис. 6.2, кривая 1). Модель фильтрации с предельным градиентом следует рассматривать как некоторую идеализацию реальных течений аномальных нефтей в пластовых условиях, для которых реологическая кривая имеет вид кривой 2 на рис. 6.2. Для сравнения на рис. 6.2 показана диаграмма ньютоновской жидкости по закону Дарси (кривая 3). 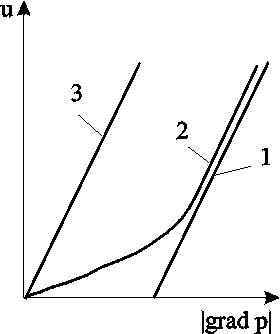 Рис. 6.2. Индикаторные линии: 1 – линейная аппроксимация неньютоновской жидкости; 2 – реальная неньютоновская жидкость; 3 – ньютоновская по закону Дарси В основе проявления неньютоновских свойств пластовых систем лежат различные физические механизмы, но все неньютоновские эффекты проявляются при малых скоростях фильтрации и в средах с малым размером пор, т.е. с малой проницаемостью. Это определяет особенности неньютоновской фильтрации в неоднородных пластах. Области малой проницаемости оказываются областями наибольшего проявления неньютоновских эффектов. Так в пластах со слоистой неоднородностью предельные градиенты различны для разных пропластков – чем больше проницаемость, тем меньше предельный градиент , и наоборот. В связи с этим, пропластки будут последовательно включаться в работу по мере того, как градиент давления будет превышать величины соответствующих предельных градиентов сдвига. Наряду с рассмотренным законом фильтрации (6.6), описывающим течение вязкопластичной жидкости в пористой среде, рассматривают степенной закон фильтрации:  , (6.7)где С – экспериментальная константа; n>0. Степенной закон, соответствующий псевдопластичному флюиду (6.4), хорошо описывает движение растворов полимеров в пористой среде и используется при расчете “полимерного” заводнения пластов с целью повышения их нефтеотдачи. 6.2. Одномерные задачи фильтрации вязкопластичной жидкости Движение аномальных нефтей в пластах по закону (6.5) приводит к существенным особенностям разработки этих пластов, не встречающимся в случае фильтрации по закону Дарси. Установившееся течение вязкопластичной жидкости. Рассмотрим плоскорадиальный приток к скважине при условии выполнения соотношения (6.4):  (u>0); (6.8) , (u=0).Решая (6.9) относительно скорости и переходя к дебиту, получим формулу притока, обобщающую формулу Дюпюи.  , если  . (6.9)u=0, если dp/dr. Считая давления на забое скважины и на границе пласта постоянными (р(rc)=рc; р(rк)=рк ), после интегрирования (6.10) находим: 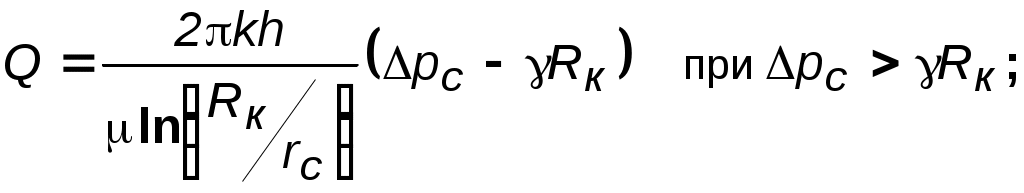  , (6.10) (6.12) Формулы (6.11), (6.12) представляют, соответственно, распределение давления в пласте и дебит скважины. Из формулы (6.11) видно, что часть разности давлений в виде линейного слагаемого с угловым коэффициентом теряется на преодоление предельного градиента сдвига. При Q0, как следует из (6.11), давление не постоянно (как в случае фильтрации по закону Дарси), а изменяется по линейному закону. При тех же условиях наличие предельного градиента давления в пласте ведет к уменьшению дебита скважины по сравнению с фильтрацией по закону Дарси (формула Дюпюи), а индикаторная линия скважины Q(рс) – прямолинейная, но не проходит через начало координат, а отсекает на оси депрессий отрезок, равный Rк (рис. 6.3а).В случае слоистого пласта с гидродинамически изолированными пропластками, т. е. при отсутствии перетоков между слоями с разными проницаемостями, для дебита в каждом пропластке справедлива формула (6.12), но своими значениями толщин, проницаемости и начального градиента. Индикаторная линия в этом случае представляется ломаной (рис. 6.3b). 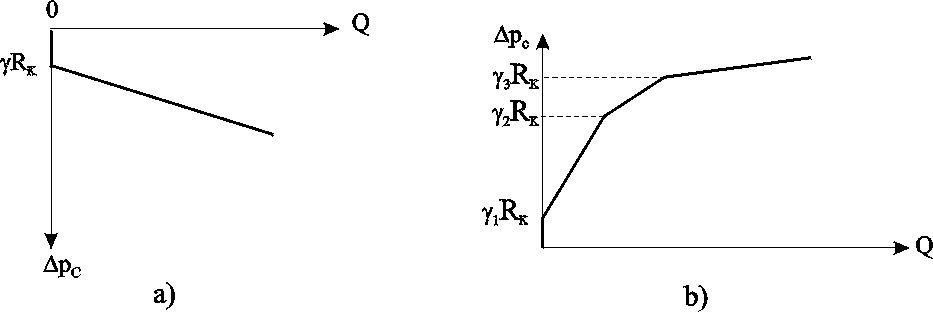 Рис. 6.3. Индикаторные линии при плоскорадиальном течении вязкоплоастичной жидкости: а – однослойный пласт; b – трёхслойный пласт Неустановившаяся фильтрация вязкопластичной жидкости. Дифференциальные уравнения для определения давления при упругом режиме работы пласта можно получить, дополняя закон фильтрации с предельным градиентом (6.5) уравнениями неразрывности и состояния флюида. Описанным в разделе 5 подходе получим следующее уравнение пьезопроводности:  , (6.13)где æ – коэффициент пьезопроводности. Уравнение (6.13) служит основой для построения нелинейной теории упругого режима вязкопластичной жидкости. Вместе с тем следует иметь в виду, что при решении нестационарных задач на основе модели фильтрации с предельным градиентом в пласте образуется переменная область фильтрации, на границе которой (пока она не достигнет границы пласта) модуль градиента давления должен равняться предельному градиенту , а давление – начальному пластовому. Если рассмотреть задачу о пуске скважины с постоянным дебитом при фильтрации вязкопластичной жидкости с предельным градиентом, то получим из решения уравнения (6.13) следующую зависимость забойного давления от времени:  . (6.14)В данной формуле логарифмический член играет основную роль при малом времени, когда преобладают упругие силы. При больших значениях времени закон движения границы возмущенной области подчиняется степенному закону. Таким образом, при некоторых значениях параметров оказывается, что основное значение имеет степенной член, так что закон падения давления на забое скважины изменяется с логарифмического на степенной. Следовательно, при больших временах вид кривых изменения забойного давления рс(t) при фильтрации с предельным градиентом существенно изменяется по сравнению с фильтрацией упругой жидкости, что позволяет обнаружить в пластовых условиях проявление предельного градиента давления. 6.3. Образование застойных зон при вытеснении нефти водой 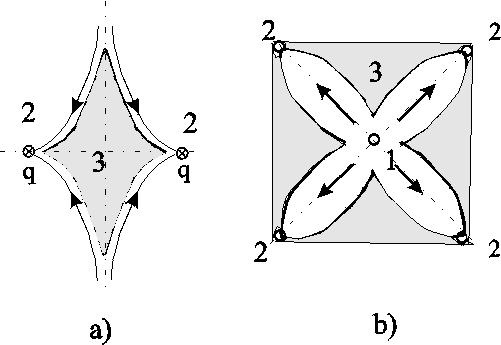 Рис. 6.4. Схемы образования застойных зон а – между двумя добывающими скважинами; b – при пятиточечной расстановке скважин (1 – нагнетательная скважина; 2 – добывающая скважина; 3 – зона застоя) Важный эффект фильтрации с предельным градиентом давления – возможность образования в пласте застойных зон (движение жидкости или газа отсутствует), при градиенте давления меньшего предельного. Возникновение застойных зон ведет к уменьшению нефтеотдачи пластов. На рис. 6.4,а застойная зона 3, расположенная между двумя добывающими скважинами с равными дебитами, затемнена. При разработке нефтяных месторождений с поддержанием пластового давления путём закачки воды тоже образуются застойные зоны. На рис. 6.4,b приведена схема вытеснения с пятиточечной системой расположения скважин. Анализ возникающего при этом двумерного течения показывает, что в зонах 3 (рис. 6.4b) скорость течения будет мала по сравнению со скоростями течения в областях, прилегающих к прямым, соединяющим нагнетательную и добывающие скважины. Поэтому эти зоны и окажутся застойными. Отношение незаштрихованных областей на рис.6.4b ко всей площади пятиточечной ячейки можно считать площадным коэффициентом охвата пласта заводнением. Величина застойной зоны и коэффициент охвата пласта зависят от параметра  , где Q – дебит добывающей скважины; L – характерный размер (например, половина расстояния между соседними скважинами).Коэффициент охвата пласта увеличивается с увеличением параметра . Вместе с тем следует отметить, что для установления чистого эффекта изменения коэффициента охвата из-за предельного градиента давления применительно к реальному месторождению необходимы исследования, позволяющие исключить влияние ряда других причин, связанных с деформацией горных пород, неоднородностью пласта, физико-химическими явлениями и т. п. ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ Закон Ньютона и его графическое представление. Классы Неньютоновских жидкостей. Стационарно реологические жидкости. Нестационарно реологические жидкости. Вязкоупругие жидкости. Виды стационарно реологических жидкостей. Вязкопластичные жидкости. Псевдопластичные жидкости. Дилатантные жидкости. Закон фильтрации вязкопластичной жидкости. Степенной закон фильтрации. Уравнение притока для вязкопластичной жидкости и его отличие от уравнения Дюпюи. Уравнение пьезопроводности для вязкопластичной жидкости. Описать изменение забойного давления во времени в случае вязкопластичной фильтрации. Образование застойных зон при вытеснении нефти водой. |