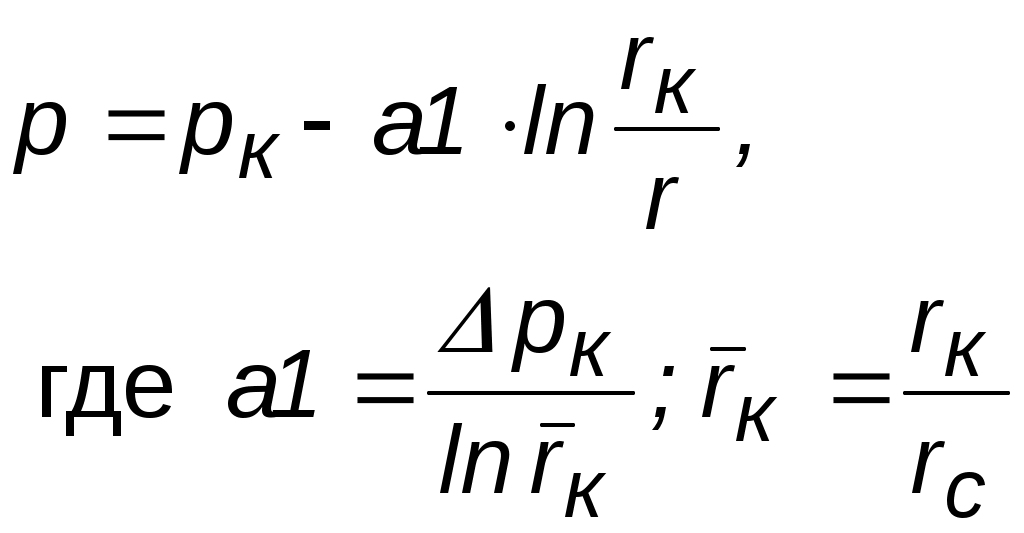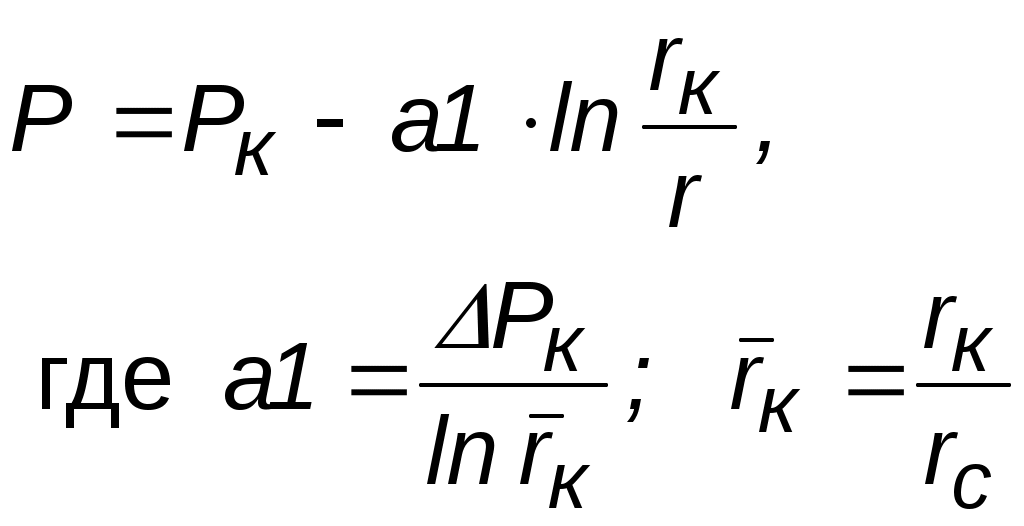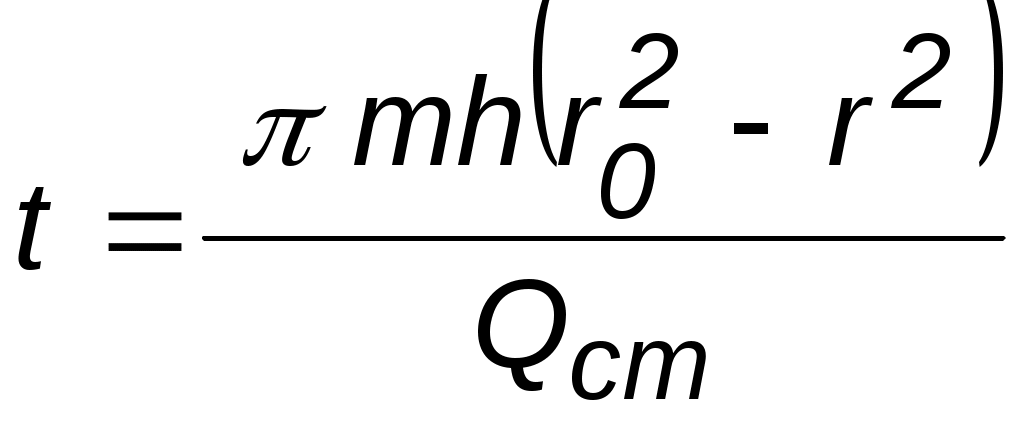Подземная гидромеханика
 Скачать 3.56 Mb.
|
|
1* –  , где * ≈ 0,01.10-5 –0,006.10-5 м2/н.;2* – =const; μ =const  ;  ;3* – р=z R T –; μ =const;  .Таблица 3.2
Проанализировав вышеприведенную таблицу, можно получить следующие зависимости потенциала от давления: Таблица 3.3
3.2.4. Анализ основных видов одномерного течения Для практического исследования фильтрационных потоков необходимо знать распределение не абстрактной функции – потенциала, а конкретных физических параметров – давления, скорости, закона движения и так далее. Следовательно, необходим переход от зависимостей (3.3, 3.7–3.10) к соотношениям, определяющим вышеперечисленные параметры при использовании приведенных в разделе 3.2.3. выражений для потенциальной функции. При этом рассмотрим только случай плоскорадиального течения, так как оно имеет наибольший практический интерес. Течение несжимаемой жидкости через недеформируемый (пористый) пласт. Выражение для потенциала (2.5) запишется в виде  .Выпишем ранее выведенные соотношения в случае плоскорадиального течения для: распределения потенциала 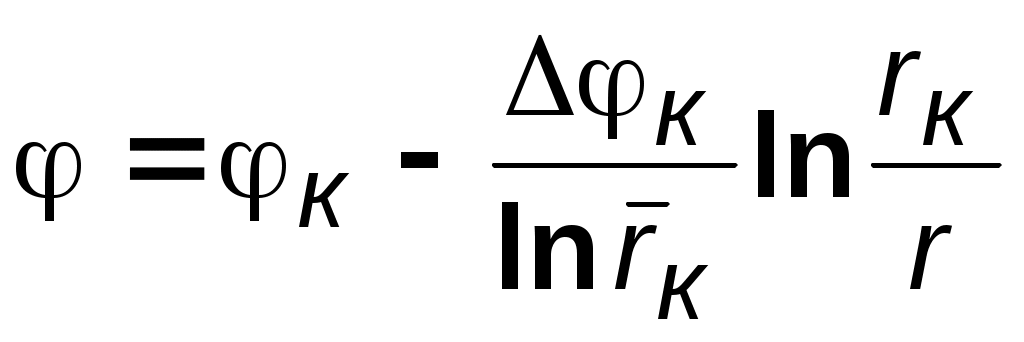 ;распределения градиента потенциала  ;дебита 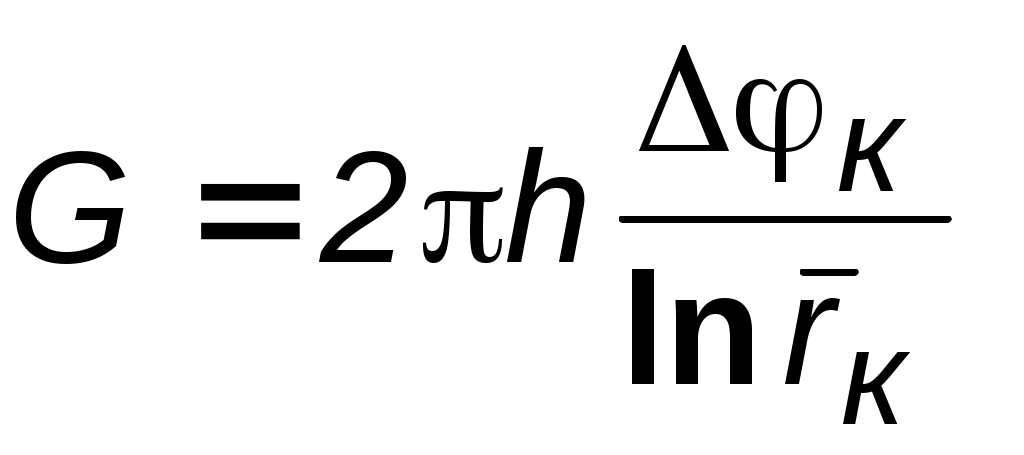 ;средневзвешенного давления  .В вышеприведенных соотношениях:  .Для определения закона движения частиц жидкости проинтегрируем уравнение движения  по времени от 0 до t и по расстоянию от r0 до r, где r0 – начальное положение частицы флюида.Переходя в вышеприведенных соотношениях от потенциала к давлению, получим искомые выражения, позволяющие провести исследование в физических переменных (табл. 3.3). Таблица 3.3
Примечание. При выводе соотношения для средневзвешенного давления интеграл не берется в конечном виде. Поэтому подинтегральное выражение приводится к виду  и раскладывается в ряд Тейлора. Беря первые два члена ряда, а именно, 1 –х/2, получаем выражение, которое можно интегрировать по частям. После пренебрежения членами с r2c получаем вышеприведенное соотношение.Уравнение притока в случае плоскорадиального течения получило название – соотношение Дюпюи. Анализ 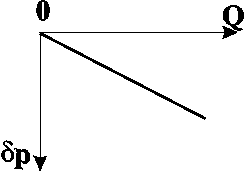 рк Рис. 3.4. Индикаторная диаграмма в случае плоскорадиального течения несжимаемой жидкости в недеформируемом пласте по закону Дарси Дебит Q не зависит от r, а только от депрессии рк. График зависимости Q от р (рис.3.4) называется индикаторной диаграммой, а сама зависимость – индикаторной. Отношение дебита к депрессии называется коэффициентом продуктивности скважины 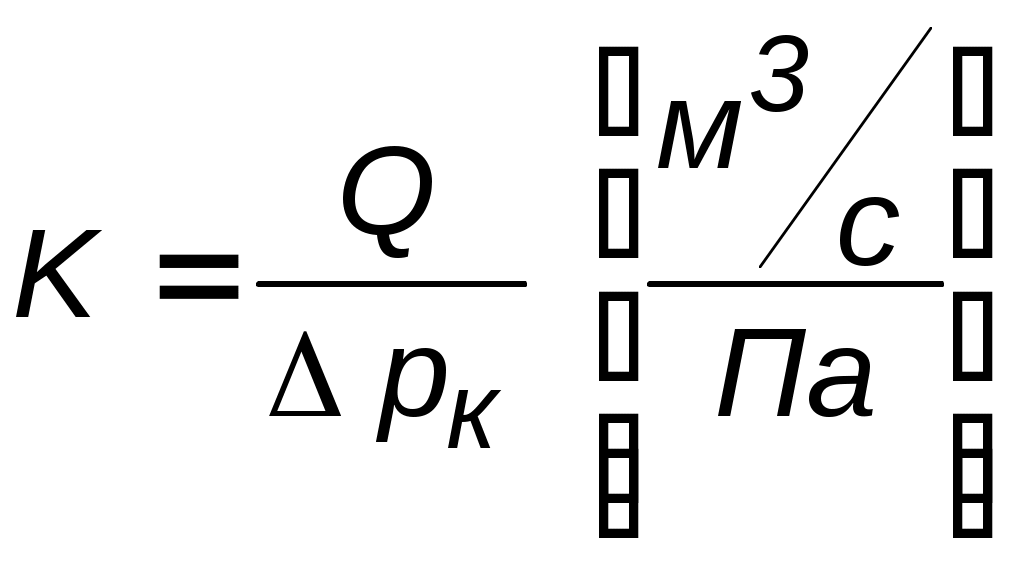 . (3.11)2. Градиент давления 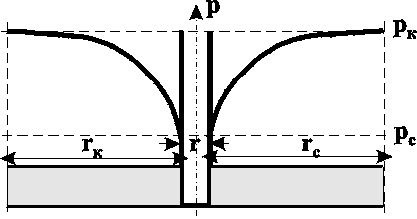 и, следовательно, скорость u обратно пропорциональны расстоянию (рис.3.5) и образуют гиперболу с резким возрастанием значений при приближении к забою. Рис. 3.6. Распределение давления по радиусу 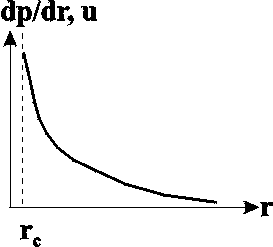 Рис. 3.5. Зависимость градиента давления и скорости от расстояния до центра скважины 3. Графиком зависимости р=р(r) является логарифмическая кривая (рис.3.6), вращением которой вокруг оси скважины образуется поверхность, называемая воронкой депрессии. Отсюда, основное влияние на дебит оказывает состояние призабойной зоны, что и обеспечивает эффективность методов интенсификации притока. 4. Изобары – концентрические, цилиндрические поверхности, ортогональные траекториям. 5. Дебит слабо зависит от величины радиуса контура rк для достаточно больших значений rк /rc, т.к. rк /rc входят в формулу под знаком логарифма. Течение совершенного газа через недеформируемый пласт. Выражение для потенциала (2.5) запишется в виде  .Выпишем соотношения для: распределения потенциала  ;распределения градиента потенциала  ;дебита  ;средневзвешенного давления  .В вышеприведенных соотношениях:  .Для определения закона движения частиц жидкости проинтегрируем уравнение движения  по времени от 0 до t и по расстоянию от r0 до r, где r0 – начальное положение частицы флюида.Переходя в вышеприведенных соотношениях от потенциала к давлению, получим искомые выражения, позволяющие провести исследование в физических переменных (табл. 3.3). Таблица 3.4
Анализ Распределение давления. Если сравнить распределения давления в случае потока газа с соответствующим распределением для однородной несжимаемой жидкости (рис. 3.7), то увидим, что для газа давление вблизи стенок скважины изменяется более резко, чем для несжимаемой жидкости. Пьезометрическая кривая для газа имеет, следовательно, более пологий характер на большем своём протяжении, чем кривая несжимаемой жидкости; однако у неё более резкий изгиб у стенки скважины, чем у кривой несжимаемой жидкости. 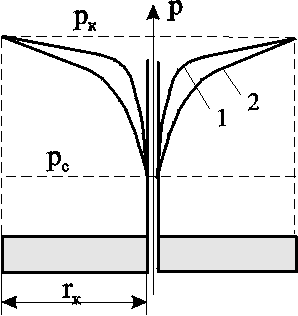 Рис. 3.7. Распределение давления при плоскорадиальном течении в недеформируемом пласте: 1 – газ; 2 – несжимаемая жидкость Уравнение притока (уравнение индикаторной линии). Индикаторная зависимость для газа описывает параболическую зависимость дебита Qст от депрессии рk (рис.3.8) и линейную зависимость дебита от разницы квадратов пластового и забойного давлений в отличие от индикаторной зависимости для несжимаемой жидкости, где устанавливается линейная связь дебита с депрессией. Уравнение притока устанавливает линейную связь между дебитом и разностью квадратов контурного и забойного давлений, поэтому для простоты исследований индикаторная диаграмма при фильтрации идеального газа по закону Дарси строится в координатах Qст (рk2-рс2). В этом случае имеем прямую линию (рис.3.9), проходящую через начало координат с угловым коэффициентом 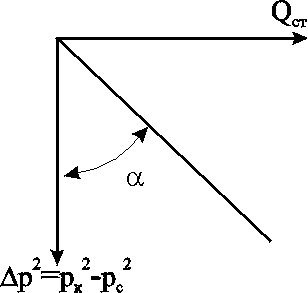 . (3.12)  Рис. 3.9. Индикаторная завиимость при фильтрации газа по закону Дарси в переменных Q – p2 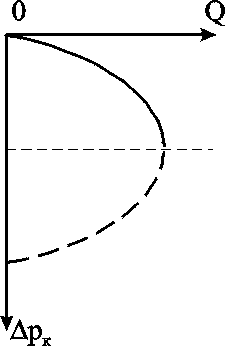 Рис. 3.8. Индикаторная зависимость при фильтрации газа по закону Дарси Запишем уравнение притока в координатах Qст (рк-рс). Так как Qcт=(рк2-рс2), а разность квадратов рк2-рс2=2ркрс - (рс)2, где рс= рк - рс , то  .Таким образом, для случая фильтрации совершенного газа по закону Дарси, имеем параболу с осью, параллельной оси дебитов (рис.3.8). Ветвь параболы, изображенная пунктиром, физического смысла не имеет. Распределение градиента давления. Градиент давления вблизи забоя резко возрастает как за счёт уменьшения r, так и за счёт падения давления р, вызванного сжимаемостью газа. Изменение скорости фильтрации получим из закона Дарси  . (3.13)Из (3.13) видно, что скорость фильтрации слабо меняется вдали от скважины и резко возрастает в призабойной зоне. |
, где 
;
, т.к. 
