Позиционные системы счисления

• Название: Позиционные системы счисления
• Дата: 18.04.2022
• Размер: 0.83 Mb.
• Имя файла: ege14 3.doc
• Тип: Документы; #483521
• страница: 3 из 14

Ещё пример задания:

Р-23. (М.В. Кузнецова) Значение арифметического выражения: 9⁹ – 3⁹ + 9¹⁹ – 19 записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?

Решение:

1. 
   Приведём все числа к степеням тройки, учитывая, что 19=27-8=3³-(2∙3¹+2∙3⁰):
   

9⁹ – 3⁹ + 9¹⁹ – 19= (3²)⁹ – 3⁹ + (3²)¹⁹ – (3³ – (2∙3¹ + 2∙3⁰)) = 3¹⁸ – 3⁹ + 3³⁸ – 3³ + 2∙3¹ + 2∙3⁰

2. 
   Перепишем выражение, располагая степени тройки в порядке убывания:
   3¹⁸ – 3⁹ + 3³⁸ – 3³ + 2∙3¹ + 2∙3⁰ = 3³⁸ + 3¹⁸ – 3⁹ – 3³ + 2∙3¹ + 2∙3⁰
   
3. 
   Сначала рассмотрим часть выражения, в которой имеется два расположенных подряд «минуса»: 3¹⁸ - 3⁹ ‑ 3³:
   
   1. 
      найдём разность двух крайних чисел: 3¹⁸ – 3³, в её троичной записи 18 – 3=15 «двоек» и 3 «нуля»;
      
   2. 
      вычтем из этого числа значение 3⁹: одна из «двоек» (на 10-й справа позиции) уменьшится на 1, остальные цифры не изменятся;
      
   3. 
      итак, троичная запись разности 3¹⁸ – 3⁹ – 3³ содержит 15 – 1=14 «двоек», одну «единицу» и 3 «нуля»
      
4. 
   Прибавим к полученному значению сумму: 2∙3¹ + 2∙3⁰ = 22₃. В троичной записи результата два крайних справа нуля заменяются на «двойки», остаётся один ноль. Общее количество «двоек»: 14+2=16.
   
5. 
   Прибавление значения 3³⁸ не изменит количества «двоек» в троичном числе: слева от имеющихся цифр появятся ещё 38 – 18=20 «нулей» и одна «единица» – на 39-й справа позиции.
   
6. 
   Итак, результат, записанный в троичной системе, содержит 39 цифр. Его состав: 16 «двоек», 2 «единицы» (их позиции: 39-я и 10-я справа) и 21 «нуль» (39-16-2=21).
   
7. 
   Ответ: 16.
   

Ещё пример задания:

Р-22. Значение арифметического выражения: 9⁸ + 3⁵ – 9

записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?

Решение:

1. 
   приведём все слагаемые к виду 3^N и расставим в порядке убывания степеней:
   

9⁸ + 3⁵ – 9 = 3¹⁶ + 3⁵ – 3²

2. 
   первое слагаемое, 3¹⁶, даёт в троичной записи одну единицу – она нас не интересует
   
3. 
   пара 3⁵ – 3² даёт 5 – 2 = 3 двойки
   
4. 
   Ответ: 3.
   

Решение (программа, Б.С. Михлин):

1. 
   задача может быть решена с помощью программы на Python, где есть встроенная поддержка длинных чисел:
   

x = 9**8+3**5-9

x3 = ''

while x:

x3 = str(x%3) + x3

x //= 3

print( 'Ответ:', x3.count('2') )

2. 
   вариант без использования символьных строк:
   

x = 9**8+3**5-9

count2 = 0

while x:

if x % 3 == 2:

count2 += 1

x //= 3

print( 'Ответ:', count2 )

3. 
   Ответ: 3.
   

Решение (электронные таблицы, Б.С. Михлин):

1. 
   эта конкретная задача может быть решена с помощью электронных таблиц
   
2. 
   Замечание. Электронные таблицы имеют ограничения при работе с длинными целыми числами. Например, Excel при вводе больших чисел заменяет все цифры после 15-го разряда на нули. Это легко проверить, введя в ячейку число с более чем 15-ю разрядами.
   

Обычно электронные таблицы при этом переходят к экспоненциальному (научному) формату. Если число больше, чем 10¹⁵, то оно хранится как вещественное число (неточно). Это ограничивает использование электронных таблиц. В этой задаче заданное число меньше, чем 10¹⁵, поэтому использовать электронные таблицы можно.

3. 
   введём заданное число, заданное арифметическим выражением, в ячейку электронной таблицы: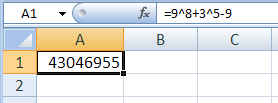
   

4. 
   выполним алгоритм перевода числа в троичную систему: найдём в B1 остаток от деления числа на 3, а в A2 – частное: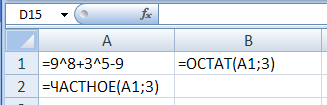
   

5. 
   скопируем формулы из А2 и В1 вниз до того момента, когда частное станет равно 0 (это означает окончание процесса перевода):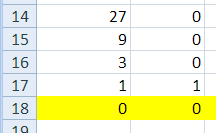
   

6. 
   подсчитаем в столбце В число остатков, равных 2: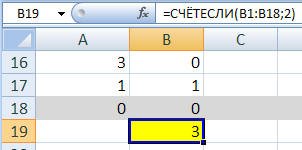
   

7. 
   Ответ: 3.
   
8. 
   в OpenOffice Calc нужно использовать такие формулы:
   

в A2: =QUOTIENT(A1;3)
в B1: =MOD(A1;3)

в B19: =COUNTIF(B1:B18;2)