|
|
Позиционные системы счисления
Еще пример задания:
Р-11. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25, запись которых в системе счисления с основанием четыре оканчивается на 11?
Общий подход:
-
вспомним алгоритм перевода числа из десятичной системы в систему с основанием  (см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на (см. презентацию), из него следует, что младшая цифра результата – это остаток от деления исходного числа на  , а две младших цифры – это остаток от деления на , а две младших цифры – это остаток от деления на 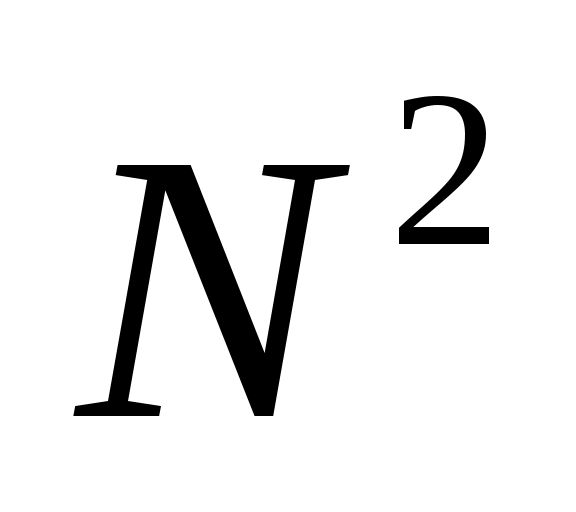 и т.д. и т.д.
-
в данном случае 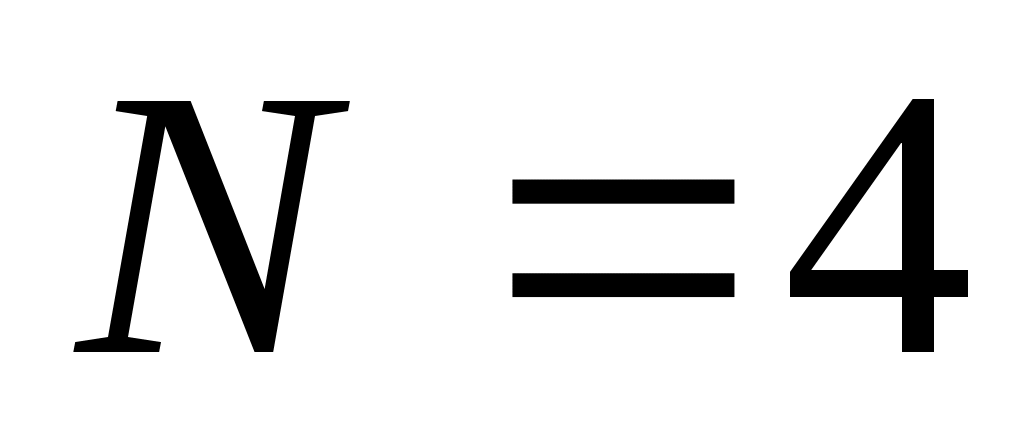 , остаток от деления числа на , остаток от деления числа на 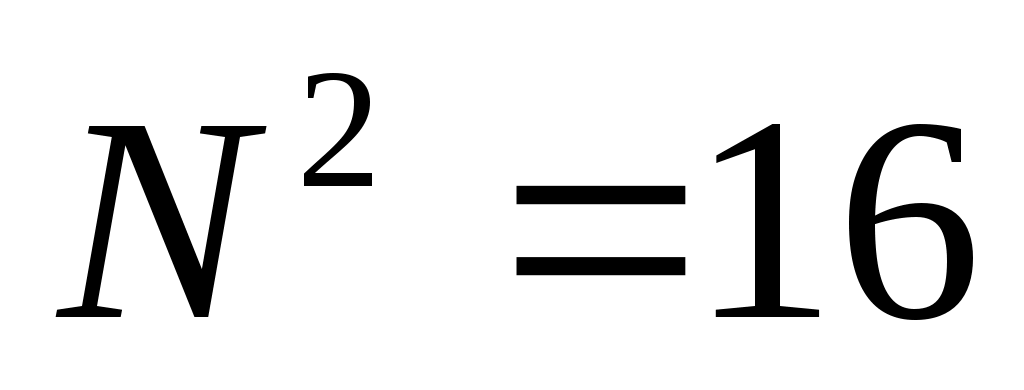 должен быть равен 114 = 5 должен быть равен 114 = 5
-
потому задача сводится к тому, чтобы определить все числа, которые меньше или равны 25 и дают остаток 5 при делении на 16
Решение (вариант 1, через десятичную систему):
-
общий вид чисел, которые дают остаток 5 при делении на 16:
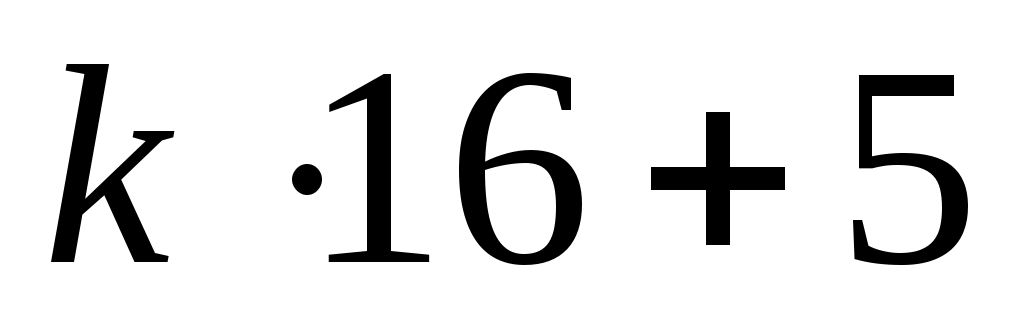
где 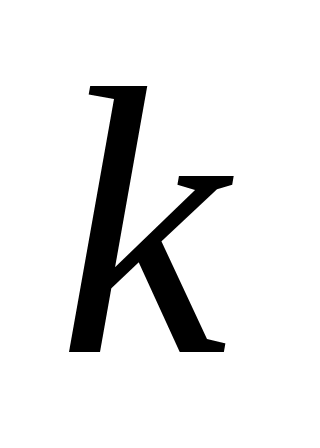 – целое неотрицательное число (0, 1, 2, …) – целое неотрицательное число (0, 1, 2, …)
-
среди всех таких чисел нужно выбрать те, что меньше или равны 25 («не превосходят 25»); их всего два: 5 (при 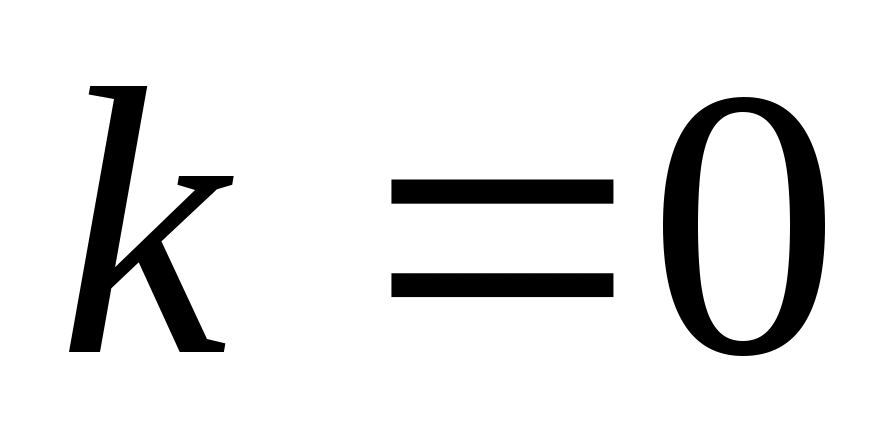 ) и 21 (при ) и 21 (при 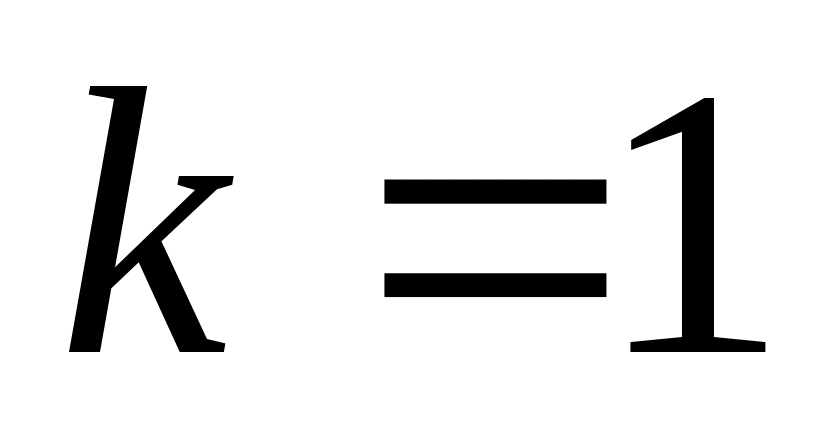 ) )
-
таким образом, верный ответ – 5, 21 .
-
Решение (вариант 2, через четверичную систему, предложен О.А. Тузовой):
-
переведем 25 в четверичную систему счисления: 25 = 1214, все интересующие нас числа не больше этого значения
-
из этих чисел выделим только те, которые заканчиваются на 11, таких чисел всего два:
это 114 = 5 и 1114 = 21
-
таким образом, верный ответ – 5, 21 .
-
Возможные ловушки и проблемы:
-
есть риск случайно «забыть» какое-то число или найти «лишнее» (в данном случае – большее 25)
-
можно сделать ошибки при переводе чисел из четверичной системы в десятичную или вообще «забыть» перевести
|
Решение (программа на Python, А.Н. Носкин):
-
можно решить задачу с помощью программы:
for i in range(1,31):# перебираем ответы
x = i
x4 = ''
while x > 0:# перевод в 4-ю систему
x4 += str(x%4)
x //=4
x4 = x4[::-1]# разворот числа
if x4[-2:]== "11":
print(i, end=",")
-
ответ: 5, 21.
Решение (программа на Python, Б.С. Михлин):
-
полная программа:
for d in '0', '1': # d - цифра (digit). При d > 1 - выход за 25
# int - переводит из 4-ой в 10-ую систему
print( int( d+'11', 4 ), end = ',' )
-
Ответ: 5, 21.
|
|
|
 Скачать 0.83 Mb.
Скачать 0.83 Mb.