прикладная математика практикум. Прикладная математика_Практикум. Практическая работа 1 Первичная статистическая обработка экспериментальных данных Пример

Название	Практическая работа 1 Первичная статистическая обработка экспериментальных данных Пример
Анкор	прикладная математика практикум
Дата	19.09.2022
Размер	1.37 Mb.
Формат файла
Имя файла	Прикладная математика_Практикум.docx
Тип	Практическая работа #685223
страница	10 из 13

1 ... 5 6 7 8 9 10 11 12 13

EXCEL. ПОИСК РЕШЕНИЯ

В Excel имеется надстройка Поиск решения, которая, в частности, помогает решать задачи линейного программирования. Необходимо воспользоваться меню Сервис – Поиск решения. Если в меню Сервис отсутствует команда Поиск решения, необходимо выполнить команду Сервис – Надстройки. Найти элемент Поиск решения и поставить галочку рядом с ним. Если в окне Надстройки нет элемента Поиск решения, необходимо доустановить Excel.

Пример.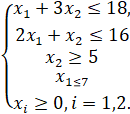

	A	B
1	Переменные
2		0
3		0
4	Целевая функция
5
6	Ограничения
7
8
9
10

Вводим эти формулы. Выделяем ячейку В5, в которой вычисляется целевая функция. Вызываем Сервис – Поиск решения. В диалоговом окне в поле ввода Установить целевую ячейку уже содержится $B$5. Установим переключатель Равной максимальному значению. Щелкнем кнопку Предположить, и в поле ввода Изменяя ячейки появится $B$2:$B$3. Щелкнем кнопку Добавить. Появится диалоговое окно Добавление ограничения. В поле ввода Ссылка на ячейку укажем $B$7. Правее в выпадающем списке с условными операторами выбираем <= (есть условный оператор ЦЕЛ, что позволяет решать задачу целочисленного программирования). В поле ввода Ограничение введем 18. Щелкнем кнопку Добавить и введем другие ограничения. ОК. Мы окажемся в диалоговом окне и увидим введенные ограничения. С помощью кнопок Изменить и Удалить мы модем изменить или удалить ограничение. Щелкнем Параметры. Установим два флажка Линейная модель и Неотрицательные значения. Ок. Выполнить.

Задание

Задание 1. Решить задачу линейного программирования.

Постановка задачи: Найти максимум и точку максимума функции Z

Z = S · x1 + G · x2

при ограничениях

– x1 / G – x2 /S + 1/4 ≤ 0

– S · x1 + 2 · G· x2 – G · S ≤ 0

2 · S · x1 – G· x2 – G · S ≤ 0

x1 ≥ 0

x2 ≥ 0

Решить задачу на ЭВМ с помощью программного комплекса MATLAB.
Решить задачу геометрическим методом.

Вариант: S=________ , G=________ .

S – последняя цифра номера зачетной книжки.

G – предпоследняя цифра номера зачетной книжки.

Задание 2. Для производства двух видов продукции A и B используются материалы трех сортов. На изготовление единицы изделия A расходуется кг материала 1-го сорта, кг материала 2-го сорта, кг материала 3-го сорта. Всего имеется , , кг материалов 1-го сорта, 2-го сорта и 3-го сорта соответственно. На изготовление единицы изделия B расходуется кг материала 1-го сорта, кг материала 2-го сорта, кг материала 3-го сорта. Реализация единицы продукции B приносит прибыль рублей. Реализация единицы продукции B приносит прибыль рублей. Всего имеется , , кг материалов 1-го сорта, 2-го сорта и 3-го сорта соответственно. При каком объеме производства прибыль будет максимальна? Задачу решить двумя способами (на ЭВМ и геометрически).

Вариант выбирать в соответствии с последней цифрой номера зачетной книжки.

Таблица 4.2

В1	В2	В3	В4	В5	В6	В7	В8	В9	В0
35	27	41	50	57	31	38	45	52	61
45	36	54	63	72	41	50	50	67	77
145	117	174	200	89	130	160	189	217	246
64	52	78	91	100	57	71	84	97	110
56	43	65	76	210	50	61	71	82	93
37	28	41	49	57	21	39	46	52	59
460	360	550	640	720	410	500	590	680	770
500	400	600	700	800	450	550	650	750	850
1000	810	1210	1420	1600	910	1100	650	1500	1700
10	8	5	7	5	11	11	5	4	16
7	10	3	5	4	13	9	7	5	19

Практическая работа № 6

4. Игра с природой

Рассматривается игра с природой 5×4 с пятью стратегиями игрока:

А₁, А₂, А₃, А₄, А₅ и четырьмя вариантами условий (состояний природы): П₁, П₂, П₃, П₄. Матрица выигрышей задана таблицей 6.1

Таблица 6.1

		Состояния природы
		П₁	П₂	П₃	П₄
с т р а т е г и и	А₁	0.85	0.1	0.45	0.05
	А₂	0.20	0.25	0.15	0.30
	А₃	0.75	0.40	0.35	0.20
	А₄	0.50	0.35	0.40	0.10
	А₅	0.25	0.30	0.25	0.80

Найти оптимальное решение (стратегию), пользуясь критериями Вальда, Сэвиджа и критерием Гурвица при λ=0.6.

Решение 1. Критерий Вальда.

В каждой строке матрицы берем наименьший выигрыш (таблица 6.2)

Таблица 6.2

		С о с т о я н и я п р и р о д ы								α_i
		П₁		П₂		П₃		П₄
с т р а т е г и и	А₁		0.85		0.1		0.45		0.05		0.05
	А₂		0.20		0.25		0.15		0.30		0.15
	А₃		0.75		0.40		0.35		0.20		0.20
	А₄		0.50		0.35		0.40		0.10		0.10
	А₅		0.25		0.30		0.25		0.80		0.25

Из величин α_i максимальная равна 0.25 , следовательно, по критерию Вальда оптимальной является стратегия А₅.

2. Критерий Сэвиджа.

Строим матрицу рисков r_ij=β_j-a_ij , где

и помещаем в правом добавочном столбце максимальный риск в каждой строке (таблица 6.3). Минимальным из значений является 0.60, следовательно, по критерию Сэвиджа, оптимальной из стратегий является любая из стратегий А₃или А₅.

Таблица 6.3

		С о с т о я н и я п р и р о д ы				γ_i
		П₁	П₂	П₃	П₄
с т р а т е г и и	А₁	0	0.30	0	0.75		0.75
	А₂	0.65	0.15	0.30	0.50		0.65
	А₃	0.10	0	0.10	0.60		0.60
	А₄	0.35	0.05	0.05	0.70		0.70
	А₅	0.60	0.10	0.20	0		0.60

3. Критерий Гурвица.

Записываем в правых трех столбцах матрицы ( таблица 6.4) пессимистическую» оценку выигрыша , «оптимистическую « оценку выигрыша и их среднее взвешенное по формуле

Максимальное значение 0.47 соответствует стратегии А₅. Следовательно, по критерию Гурвица с небольшим перевесом в сторону пессимизма оптимальной стратегией является стратегия А₅.

Таблица 6.4

		С о с т о я н и я п р и р о д ы				α_i		ώ_i	h_i
		П₁	П₂	П₃	П₄			ώ_i	h_i
с т р а т е г и и	А₁	0.85	0.1	0.45	0.05		0.05	0.85	0.37
	А₂	0.20	0.25	0.15	0.30		0.15	0.30	0.21
	А₃	0.75	0.40	0.35	0.20		0.20	0.75	0.42
	А₄	0.50	0.35	0.40	0.10		0.10	0.50	0.26
	А₅	0.25	0.30	0.25	0.80		0.25	0.80	0.47

Таким образом, все три критерия говорят в пользу стратегии А₅.

1 ... 5 6 7 8 9 10 11 12 13