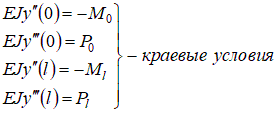прикладная математика практикум. Прикладная математика_Практикум. Практическая работа 1 Первичная статистическая обработка экспериментальных данных Пример
 Скачать 1.37 Mb. Скачать 1.37 Mb.
|
|
Задание Задание 1. Владелец небольшого магазина вначале каждого рабочего дня закупает для реализации некий скоропортящийся продукт по цене a рублей за единицу. Цена реализации этого продукта – b рублей за единицу. Из наблюдений известно, что спрос на этот продукт за день может быть равен 1,2,3 или 4 единицы. Если продукт за день не продан, то в конце дня его всегда покупают по цене c рублей за единицу. Пользуясь критериями Севиджа, Вальда, Гурвица и максимизирую ожидаемый доход, определить, сколько единиц этого продукта должен закупать владелец каждый день. Чему равна ожидаемая стоимость полной информации? Таблица 6.5
Таблица 6.6
Задание 2. Компания рассматривает вопрос о строительстве завода. Возможны три варианта действий а) Построить большой завод стоимостью М1 тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере тысяч долларов в течение следующих 5 лет) с вероятностью и низкий спрос ( ежегодные убытки тысяч долларов) с вероятностью . б) Построить маленький завод стоимостью М2 тысяч долларов. При этом варианте возможны большой спрос (годовой доход в размере тысяч долларов в течение следующих 5 лет) с вероятностью и низкий спрос (ежегодные убытки тысяч долларов) с вероятностью . в) Отложить строительство завода на один год для сбора дополнительной информации, которая может быть позитивной или негативной с вероятностью и соответственно. В случае позитивной информации можно построить заводы по указанным выше расценкам, вероятности большого и низкого спроса меняются на и соответственно. Доходы на последующие четыре года остаются прежними. В случае негативной информации компания заводы строить не будет. Нарисовать дерево решений. Определить наиболее эффективную последовательность действий и её стоимостную оценку. Таблица 6.7
Задание 3. Предприниматель провел анализ, связанный с открытием магазина. Если он откроет большой магазин, то при благоприятном состоянии рынка получит прибыль 60 млн. рублей, при неблагоприятном – понесет убытки 40 млн. руб. Маленький магазин принесет ему 0 млн. рублей прибыли при благоприятном состоянии рынка и 10 млн. рублей убытков при неблагоприятном. Возможность благоприятного и неблагоприятного состояния рынка он оценивает одинаково. Исследование рынка, которое может провести специалист, обойдется предпринимателю в 5 млн. рублей. Специалист считает, что с вероятностью 0,6 состояние рынка окажется благоприятным. В тоже время при положительном заключении состояние рынка окажется благоприятным лишь с вероятностью 0,9. При отрицательном заключении с вероятностью 0,12 состояние рынка может оказаться благоприятным. Используйте дерево решений для того, чтобы помочь предпринимателю принять решение. Следует ли заказать проведение обследования состояния рынка? Следует ли открыть большой магазин? Какова ожидаемая стоимостная оценка наилучшего решения? Практическая работа № 7 7.а) Задача об изгибе балки на упругом основании методом конечных элементов Пусть задан функционал вида:
где Условие минимума:
т.е. существует взаимно однозначное соответствие между задачей о минимуме функционала ( 7.1) и системой линейных уравнений Ax = b. 1. Общая постановка задачи об изгибе балки на упругом основании(модель Винклера). Суть модели Винклера состоит в предположении, что реакция основания 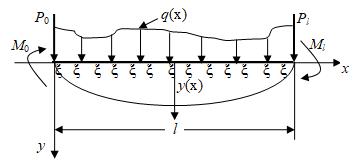 Рис. 7.1. Расчетная схема балки. Напряженно-деформируемое состояние такой балки соответствует решению задачи о минимуме следующего функционала (функционала энергии): Функция прогибов балки y(x), вызванных силами P, распределенной нагрузкой q и изгибающими моментами M, является условием минимума функционала энергии балки (т.е. принесет минимальное значение этому функционалу):
где Замечание. Из курса вариационного исчисления следует, что решение такой задачи совпадает с решением следующей краевой задачи:
что соответствует исходной постановке, обычно формулируемой в курсе «Сопротивление материалов». 2. Метод конечных элементов (МКЭ). Разобьем отрезок 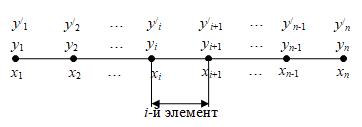 Рис. 7.2. Конечно-элементная разбивка. В каждой При этом
где 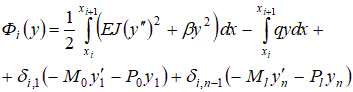 здесь 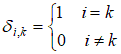 – символ Кронекера. – символ Кронекера.2.1. Локальные построения на i-ом элементе. Переходим к локальным координатам: 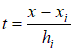 , , 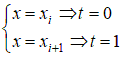 , , 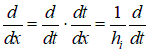 , , Представим неизвестную функцию прогиба
Для определения 4-х параметров 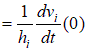 , ,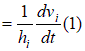 . .Поскольку
Введем следующие обозначения 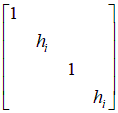 , , 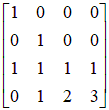 . .Тогда система уравнений (7) может быть представлена в матрично-векторном виде:
Следовательно
Легко проверить, что
Обозначим 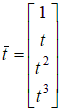 , тогда , тогда 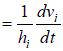 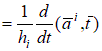 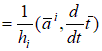 , ,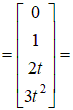 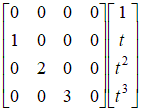 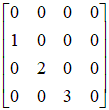 Т.е.
Далее
где 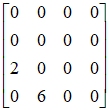
где 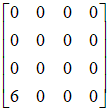
2.2. Построение локальной матрицы жесткости на i-ом элементе. С учетом представленных выше локальных построений вычислим квадратичную часть функционала
Рассмотрим общий случай 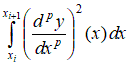 , , 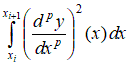 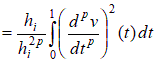 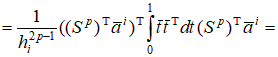 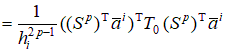 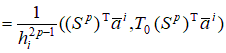 , ,где 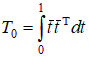 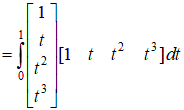 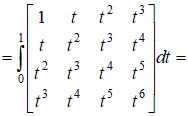 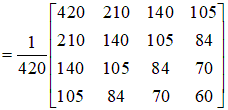 Следует заметить, что 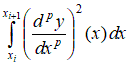 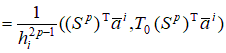 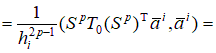 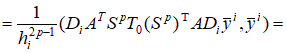 где
При
При
Таким образом 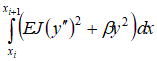
– локальная матрица жесткости 2.3. Построение локального вектора нагрузки на i-ом элементе. С учетом представленных выше локальных построений вычислим линейную часть функционала
Рассмотрим в общем случае 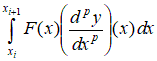 , , Полагаем, что 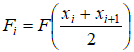 . Тогда . Тогда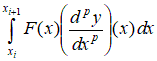 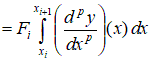 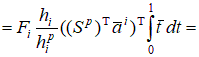 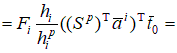 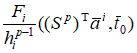 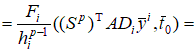 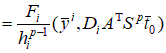 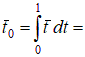 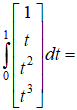
При
Таким образом,
, где 2.4. Построение глобальной матрицы жесткости и вектора нагрузки разрешающей системы. Общий функционал, представляющий сумму функционалов по элементам, с учетом представленных выше локальных построений примет вид
где Объединяя коэффициенты локальных матриц жесткости и компоненты локальных векторов нагрузок, относящихся к общим узловым значениям, получим
где матрица 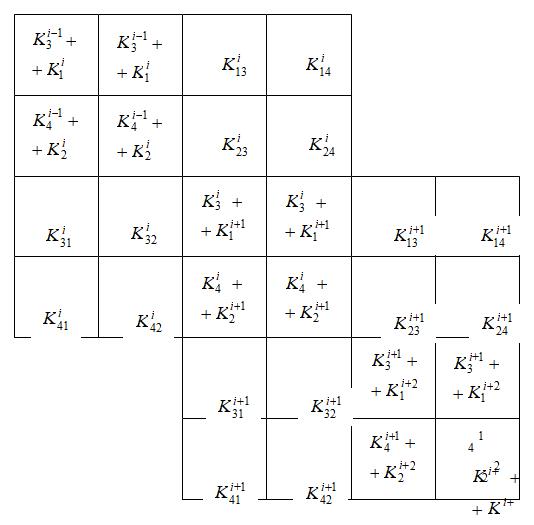 Рис. 7.3. К формированию глобальной матрицы жесткости. Замечания к рисунку 7.3. 1. 2. При 3. При 4. При 5. Представленный фрагмент матрицы Схематично формирование элементов вектора 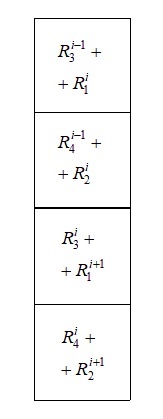 Рис. 7.4. К формированию глобального вектора нагрузки. Замечания к рисунку 7.4. 1. 2. При 3. При 4. Представленный фрагмент вектора 2.5. Учет закреплений. Пусть для некоторого узла с номером
Этому номеру соответствует порядковый номер неизвестной
Тогда для выполнения условия (26) следует приравнять нулю строку и столбец глобальной матрицы, имеющих номер
Если задано условие
Тогда порядковый номер неизвестной
Для выполнения условия (7.29) требуется произвести аналогичную предыдущему случаю коррекцию глобальной матрицы и глобального вектора нагрузки (см. формулы (7.28)), где порядковый номер неизвестной представлен формулой (7.30). 1.6. Учет краевых условий исходной постановки.
Как следует из вариационной постановки (7.3) или (7.5), т.е. 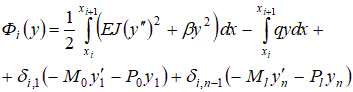 поперечные силы
Таким образом, решение исходной задачи методом конечных элементов сводится к решению системы линейных алгебраических уравнений относительно узловых неизвестных:
Задание. 1. Построить локальные векторы нагрузки. 2. Построить локальные матрицы жесткости. 3. Получить численное решение и построить графики при Варианты задания. При этом |

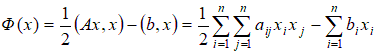
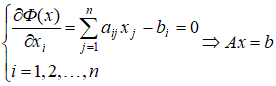
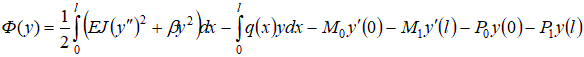
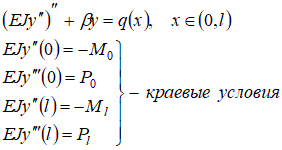
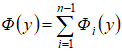
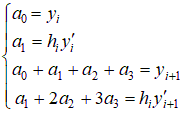
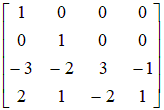
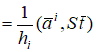
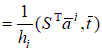
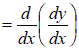
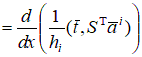
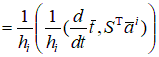
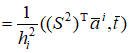
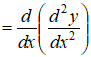
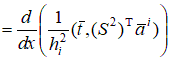
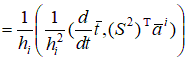
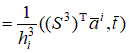
 и
и 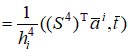
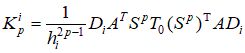
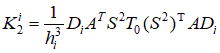
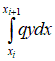
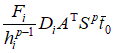 ,
, 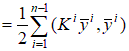
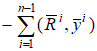 ,
,