прикладная математика практикум. Прикладная математика_Практикум. Практическая работа 1 Первичная статистическая обработка экспериментальных данных Пример
 Скачать 1.37 Mb.
|
|
Пример М-файла (для MATLAB) function beam_FEM_cubic % ввод,задание и формирование исходных данных s=input('ввести номер варианта(последняя цифра номера зачетной книжки)s='); g=input('ввести предпоследнюю цифру номера зачетной книжки g='); L=1; c=4*(s+g)/100/L^2; c1=1; EJ=c1; bt=100; n=input('ввести число точек n='); ne=n-1; %количество элементов h=L/ne; % длина элемента xs=h/2:h:L; %массив координат средних точек элементов q=c*bt*xs.*(L-xs); %массив нагрузок в средних точках элементов P0=0; M0=2*c*c1; % краевые условия слева: x=0 PL=0; ML=-M0; % краевые условия справа: x=L mp=2; %число неизвестных в узле: y(xi),y'(xi) me=2*mp;%число неизвестных на элементе: y(x_i),y'(x_i),y(x_i+1),y'(x_i+1) ns=mp*n; %общее количество неизвестных xi=0:h:L; % координаты узлов % формирование вспомогательных матриц и векторов Ag=[1 0 0 0;0 1 0 0;1 1 1 1;0 1 2 3] A=inv(Ag) S=diag([1 2 3]',-1) T0=[ 1 1/2 1/3 1/4 1/2 1/3 1/4 1/5 1/3 1/4 1/5 1/6 1/4 1/5 1/6 1/7] TT=420*T0 Di=diag([1 h 1 h]') t0=[1 1/2 1/3 1/4]' % формирование локальных матриц и векторов K0=h*Di*A'*T0*A*Di K2=1/h^3*Di*A'*S^2*T0*(S^2)'*A*Di Ke=EJ*K2+bt*K0 %локальная матрица жесткости R0=h*Di*A'*t0 %локальный вектор нагрузки % формирование глобальной матрицы жесткости Kg=zeros(ns); for i=1:mp:ns-mp-1 Kg(i:i+me-1,i:i+me-1)=Kg(i:i+me-1,i:i+me-1)+Ke(:,:); end % формирование глобального вектора нагрузки Rg=zeros(ns,1); ie=0; for i=1:mp:ns-mp-1 ie=ie+1; Rg(i:i+me-1)=Rg(i:i+me-1)+q(ie)*R0(:); end % учет граничных условий Rg(1)=Rg(1)+P0; Rg(2)=Rg(2)+M0; Rg(ns-1)=Rg(ns-1)+PL; Rg(ns)=Rg(ns)+ML; %Kg %Rg U=Kg\Rg; yi=U(1:mp:ns)'; dyi=U(2:mp:ns)'; % вычисление y, y', y" и y"' в центрах элементов for i=1:ne ys(i)=df(i,0,0.5); dy(i)=df(i,1,0.5); d2y(i)=df(i,2,0.5); d3y(i)=df(i,3,0.5); end % вычисление y" и y"' в узлах for i=1:ne d2yi(i)=df(i,2,0); d3yi(i)=df(i,3,0); end d2yi(n)=df(ne,2,1); d3yi(n)=df(ne,3,1); disp('прогиб балки'),disp(yi) disp('угол поворота'),disp(dyi) disp('изгибающий момент'),disp(-EJ*d2yi) disp('поперечная сила'),disp(-EJ*d3yi) figure(),plot(xs,ys,xs,dy,xs,-EJ*d2y,xs,-EJ*d3y),title('v centrah elementov'),grid on legend('y','dy','M=-EJ*d2y','Q=-EJ*d3y') figure(),plot(xi,yi,xi,dyi,xi,-EJ*d2yi,xi,-EJ*d3yi),title('v uzlah'),grid on legend('y','dy','M=-EJ*d2y','Q=-EJ*d3y') function dpyi=df(i,p,t) % вычисление dpy в точке t на i-м элементе Dp=(S^p)'*A*Di; ti=[1;t;t^2;t^3]; in=1+mp*(i-1);ik=in+me-1; z=U(in:ik); dpyi=dot(Dp*z,ti)/h^p; end end Результаты счета при g=3 и s=12 ввести номер варианта (последняя цифра номера зачетной книжки)s=12 ввести предпоследнюю цифру номера зачетной книжки g=3 ввести число точек n=21 Ag = 1 0 0 0 0 1 0 0 1 1 1 1 0 1 2 3 A = 1 0 0 0 0 1 0 0 –3 –2 3 –1 2 1 –2 1 S = 0 0 0 0 1 0 0 0 0 2 0 0 0 0 3 0 T0 = 1.0000 0.5000 0.3333 0.2500 0.5000 0.3333 0.2500 0.2000 0.3333 0.2500 0.2000 0.1667 0.2500 0.2000 0.1667 0.1429 TT = 420 210 140 105 210 140 105 84 140 105 84 70 105 84 70 60 Di = 1.0000 0 0 0 0 0.0500 0 0 0 0 1.0000 0 0 0 0 0.0500 t0 = 1.0000 0.5000 0.3333 0.2500 K0 = 0.0186 0.0001 0.0064 –0.0001 0.0001 0.0000 0.0001 –0.0000 0.0064 0.0001 0.0186 –0.0001 –0.0001 –0.0000 –0.0001 0.0000 K2 = 1.0e+004 * 9.6000 0.2400 –9.6000 0.2400 0.2400 0.0080 –0.2400 0.0040 –9.6000 –0.2400 9.6000 –0.2400 0.2400 0.0040 –0.2400 0.0080 Ke = 1.0e+004 * 9.6002 0.2400 –9.5999 0.2400 0.2400 0.0080 –0.2400 0.0040 –9.5999 –0.2400 9.6002 –0.2400 0.2400 0.0040 –0.2400 0.0080 R0 = 0.0250 0.0002 0.0250 –0.0002 прогиб балки 0.0003 0.0288 0.0542 0.0767 0.0961 0.1126 0.1261 0.1366 0.1440 0.1485 0.1500 0.1485 0.1440 0.1366 0.1261 0.1126 0.0961 0.0767 0.0542 0.0288 0.0003 угол поворота 0.5991 0.5391 0.4792 0.4192 0.3593 0.2994 0.2395 0.1796 0.1197 0.0599 –0.0000 –0.0599 –0.1197 –0.1796 –0.2395 –0.2994 -0.3593 –0.4192 –0.4792 –0.5391 –0.5991 изгибающий момент 1.2001 1.1995 1.1990 1.1986 1.1983 1.1980 1.1978 1.1977 1.1975 1.1975 1.1975 1.1975 1.1975 1.1976 1.1978 1.1979 1.1982 1.1985 1.1989 1.1994 1.2001 поперечная сила –0.0138 –0.0117 –0.0097 –0.0080 –0.0064 -0.0050 –0.0038 –0.0026 –0.0015 –0.0005 0.0005 0.0015 0.0026 0.0038 0.0050 0.0064 0.0080 0.0097 0.0117 0.0138 0.0138 >> Задание Задача об изгибе растянуто-изогнутой балки. Задание. Решить задачу о изгибе растянуто-изогнутой балки методом конечных элементов. Исходная постановка задачи: Найти функцию y(x) при которой функционал 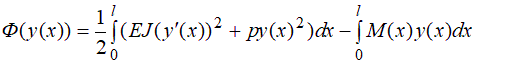 принимает минимальной значение. Составить конечно-элементную систему уравнений (матрицу жесткости и вектор нагрузки) и решить полученную систему. 1. Решить задачу на ЭВМ для N=9 точек (N-1 конечных элементов). 2. Представить результаты счета для N=9, то есть 8 конечных элементов. 3. Решить задачу вручную для N=4, т.е. 3 конечных элементов. 7.б) Задача теплопроводности. Задание. Решить задачу теплопроводности: 1. Методом конечных разностей по явной схеме (требуется составить программу в системе MATLAB и выполнить ручной счет). 2. Численно-аналитическим методом (требуется составить программу в системе MATLAB). Варианты задания. 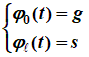 – функция, характеризующая мощность источника тепла; – краевые условия; – начальные условия; – длина;  – коэффициент температуропроводности;  – предпоследняя цифра в зачетной книжке,  – последняя цифра номера зачетной книжки.Метод конечных разностей Принять для расчета на ЭВМ число отрезков деления по длине  и количество шагов по времени  , для ручного счета –  и  . Вывести значения температуры для  :  ,  ,  ,  .Пример ручного счетадля  ,  .При  , из условия устойчивости (9)  .Начальные значения:  ,  ,  .Граничные значения:  ,  ,  .Для внутренних точек:  ,  , .Таблица 1. Результаты ручного счета Таблица 7.2
Пример М-файла. s=input('Введите s='); g=input('Введите g='); n=input('Введите n='); a=1; L=1; h=L/n; tau=h^2/(2*a); x=0:h:L; u0=g+(g+3*s)*x-2*(g+s)*x.^2; u1=u0; kprn=12; Tprn=zeros(kprn,1); Uprn=zeros(kprn,n+1); kt=0; for k=1:101 t=(k-1)*tau; if(mod(k-1,10)==0||(k-1)==1) kt=kt+1; Tprn(kt,1)=t; Uprn(kt,:)=u0; end u1(2:n)=(u0(1:n-1)+u0(3:n+1))/2; u0=u1; end fprintf('\n t значения функции температуры u(xi,t)\n') for i=1:kprn fprintf('%4.2f',Tprn(i)),fprintf('%6.2f',Uprn(i,:)),fprintf('\n') end Результаты счетадля  ,  .Введите s=12 Введите g=3 Введите n=8 t значения функции температуры u(xi, t) 0.00 3.00 7.41 10.88 13.41 15.00 15.66 15.38 14.16 12.00 0.01 3.00 6.94 10.41 12.94 14.53 15.19 14.91 13.69 12.00 0.08 3.00 5.47 7.73 9.62 11.00 11.87 12.23 12.22 12.00 0.16 3.00 4.73 6.37 7.85 9.09 10.10 10.87 11.48 12.00 0.23 3.00 4.40 5.76 7.04 8.22 9.29 10.26 11.15 12.00 0.31 3.00 4.25 5.48 6.68 7.83 8.93 9.98 11.00 12.00 0.39 3.00 4.18 5.35 6.51 7.65 8.76 9.85 10.93 12.00 0.47 3.00 4.15 5.30 6.44 7.57 8.69 9.80 10.90 12.00 0.55 3.00 4.14 5.27 6.40 7.53 8.65 9.77 10.89 12.00 0.63 3.00 4.13 5.26 6.39 7.51 8.64 9.76 10.88 12.00 0.70 3.00 4.13 5.25 6.38 7.51 8.63 9.75 10.88 12.00 0.78 3.00 4.13 5.25 6.38 7.50 8.63 9.75 10.88 12.00 >> 2. Численно-аналитический метод Принять для расчета на ЭВМ число внутренних точек по   и значения по времени , , ,  . Построить графики для ,  .Поскольку , а также  и  – константы, вектор  – не зависит от  . В этом случае формула (7.32) преобразуется к виду
Выполняем интегрирование: 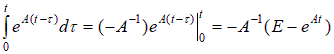 . Таким образом, решение задачи приводится к виду
|
,
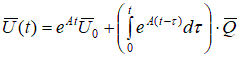