прикладная математика практикум. Прикладная математика_Практикум. Практическая работа 1 Первичная статистическая обработка экспериментальных данных Пример
 Скачать 1.37 Mb.
|
|
Практическая работа № 3 3. Многомерная линейная регрессионная модель Пример. На прессе определяли прочность образцов в возрасте 28 суток в зависимости от времени изотермической выдержки. Каждый опыт проводился на трех образцах. Результаты эксперимента занесены в таблицу 3.1. Проверим, можно ли считать значимым коэффициент корреляции между прочностью и временем изотермической обработки. Таблица 3.1 Оценка значимости коэффициента корреляции
Диаграмма рассеяния в данном случае имеет вид: 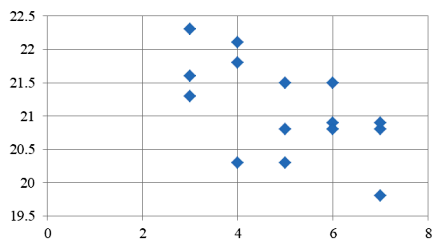 Рисунок 1.2 – Диаграмма рассеяния Найдем выборочный коэффициент корреляции по формуле : 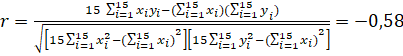 Проверим гипотезу об отсутствии корреляционной связи, для этого вычислим статистику Стьюдента 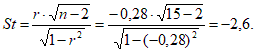 По таблице 1 в Справочных материалах найдем  – критическое значение распределения Стьюдента, задав уровень значимости 0,05 (число степеней свободы равно 13): Значение статистки меньше критического, поэтому считаем, что коэффициент корреляции значимо отличается от нуля. Получим линейную модель связи между прочностью и временем изотермической выдержки. Рассчитаем коэффициенты линейной регрессии, для этого предварительно найдем:  Тогда 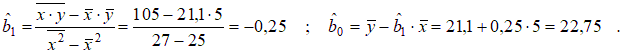 Таким образом, уравнение линейной регрессии имеет вид:  Рассеяние вокруг линии регрессии: 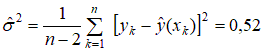 Оценим качества построенной модели: 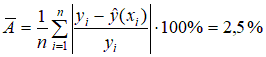 Средняя ошибка аппроксимации меньше допустимого предела в 10%. 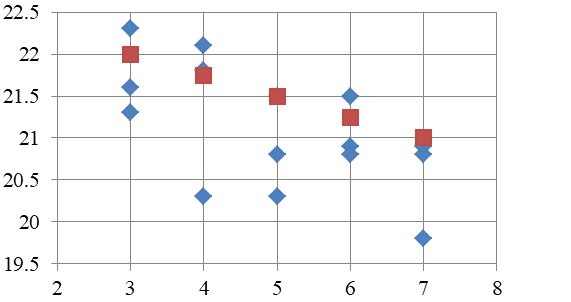 Рисунок 1.13 – Диаграмма рассеяния Задание Определить уравнение множественной линейной регрессии. Оценить качество подгонки и значимость полученного уравнения в целом. Определить среднюю относительную ошибку для построенной модели. Расположить объясняющие факторы по убыванию корреляционной связи с объясняемой переменной. Провести анализ полученных результатов. Вариант 1. Таблица 3.2
Вариант 2. Таблица 3.3
Вариант 3. Таблица 3.4
Практическая работа № 4 4. Задача линейного программирования Пример. Составление задачи линейного программирования состоит из следующих этапов: выбор переменных; составление ограничений задачи на выбранные переменные; запись целевой функции. Математическую формализацию задачи линейного программирования рассмотрим на примере задачи о выборе оптимального плана: в обработку поступило 3 партии металлических прутов длинной 8,5; 6,0; 5,0 м. В первой партии 40 прутов, во 2-ой – 20, а в 3-й – 50. Прутки распиливают на комплекты, состоящие из 4-х заготовок: 2 заготовки по 3 м и 2 заготовки по 2 м. Необходимо распилить все прутки так, чтобы получить возможно большее число комплектов. Решение. Составим таблицу всех возможных способов распиливания прутков на заготовки Таблица 4.1
Введем следующие переменные:  – количество прутов, распиленных по первому способу; – количество прутов, распиленных по второму способу;…  – количество прутов, распиленных по восьмому способу; – число комплектов.Количество прутков, распиленных по каждому способу, и число комплектов, очевидно, должны быть неотрицательными, т.е.  .Ограничения задачи: 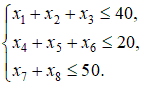 Первое ограничение означает, что количество металлических прутков, распиленных по 1-му, 2-му и 3-му способам, не должно превышать общего количества прутков первой партии. Аналогичный смысл имеют два других неравенства. Так как в комплект входит 2 заготовки по 3 м, то их общее количество, т.е.  должно быть не менее удвоенного числа комплектов: Аналогично для заготовок длиной по 2 м должно выполняться неравенство вида  В задаче требуется получить возможно большее число комплектов, поэтому целевая функция будет иметь вид  Итак, рассмотренная задача линейного программирования формулируется следующим образом: Найти такие значения переменных , при которых достигается максимум значения целевой функции  и выполняются ограничения вида 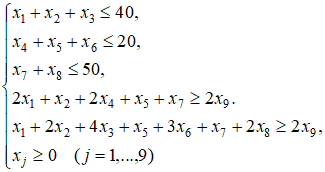 Пример. Привести задачу линейного программирования к каноническому виду. Задача линейного программирования в канонической форме имеет следующий вид: 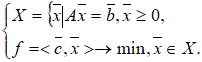 Следовательно, при переходе к каноническому виду необходимо: Наложить условие неотрицательности на переменные (свободные переменные представляются разностью двух неотрицательных переменных  );Перейти к ограничениям-равенствам (вводя дополнительные переменные); Перейти к задаче минимизации целевой функции. Привести к каноническому виду следующую задачу линейного программирования: 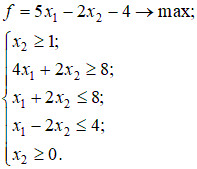 Решение. Свободную переменную представляем в виде разности двух неотрицательных переменных  и  ,  : Все ограничения-неравенства приводим к виду ≥0: 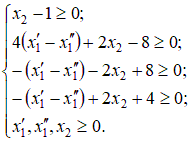 Вводя дополнительные переменные 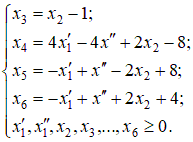 , перейдем к ограничениям-равенствам: Перейдем к задаче минимизации целевой функции: 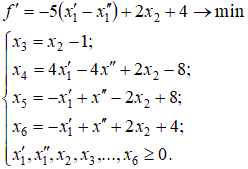 Таким образом, задача линейного программирования в канонической форме имеет следующий вид: Пример. Геометрическое решение задачи линейного программирования. Рассмотрим основную задачу линейного программирования: 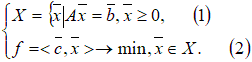 Геометрический метод решения задачи линейного программирования применяется при  , т.е. в пространстве  (иногда и при  ) и состоит из двух этапов:Построение области допустимых решений (ОДР) – множества  :а) записать уравнения граничных прямых и построить их графики; б) выделить область решения каждого из неравенств системы ограничений (1); в) выделить область допустимых решений; поиск оптимального решения: г) построить вектор градиента целевой функции (2) и линию её уровня; д) параллельным переносом линии уровня целевой функции в направлении, противоположном направлению градиента, найти оптимальное решение. Решить геометрически следующую задачу линейного программирования: 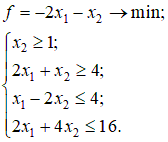 Решение. 1) Построение области допустимых решений: а) записываем уравнения граничных прямых и строим их графики; 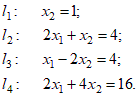 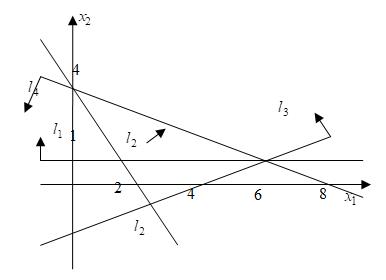 Рис 4.1 . Построение области допустимых решений б) используя произвольные пробные точки (удобнее всего брать точку О(0;0)), выделяем полуплоскости – области решения каждого из неравенств системы (1) (полуплоскости отмечены стрелками на соответствующих прямых); в) строим область допустимых решений – множество 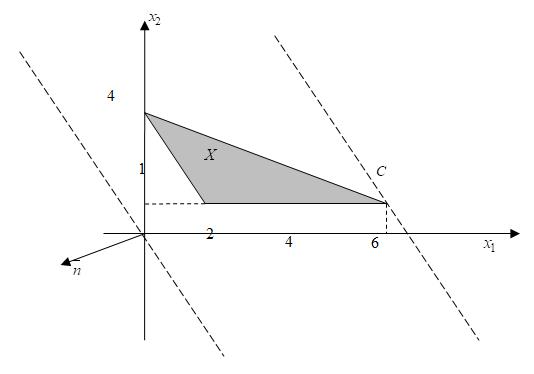 – как пересечение полученных полуплоскостей; рис 4.2 Область допустимых решений 2) поиск оптимального решения: г) построить вектор градиента целевой функции  и линию уровня целевой функции, т.е. прямую, перпендикулярную вектору  ;д) параллельно перемещая линию уровня в направлении, противоположном направлению градиента, определяем оптимальную точку  . Значение целевой функции в точке  равно Ответ:  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||