прикладная математика практикум. Прикладная математика_Практикум. Практическая работа 1 Первичная статистическая обработка экспериментальных данных Пример

• Название: Практическая работа 1 Первичная статистическая обработка экспериментальных данных Пример
• Анкор: прикладная математика практикум
• Дата: 19.09.2022
• Размер: 1.37 Mb.
• Имя файла: Прикладная математика_Практикум.docx
• Тип: Практическая работа; #685223
• страница: 13 из 13

Пример М-файла

function temperatura

function U=ut(t)

 E=eye(n); eAt=expm(t*A);

 U=eAt*U0-A\(E-eAt)*Q;

end

s=input('ввести s=');

g=input('ввести g=');

n=input('ввести количество внутренних точек n=');

L=input('ввести L=');

alpha=input('ввести alpha=');

h=L/(n+1);

c=alpha/h^2;

a1=ones(n-1,1);

A=diag(a1,-1)-2*eye(n)+diag(a1,1);A=c*A;

u0=g; ul=s;

Q=c*[u0;zeros(n-2,1);ul];

xi=(0:h:L)';x=xi(2:n+1);

U0=g+(g+3*s)*x-2*(g+s)*x.^2;

t=[[0 1],10:10:100]/(2*c);

nt=length(t);res=zeros(nt,n+2);

fprintf('\n значения функции температуры u(xi,t)\n')

for i=1:nt

 res(i,:)=[u0 ut(t(i))' ul];

 fprintf('U(%4.2f):',t(i)),fprintf('%6.2f',res(i,:)),fprintf('\n')

end

plot(xi,res(1,:),xi,res(4,:),xi,res(nt,:)),grid on

s1=sprintf('t=%2.0f',t(1));

s2=sprintf('t=%4.2f',t(4));

s3=sprintf('t=%4.2f',t(nt));

legend(s1,s2,s3,0)

title(sprintf('temperatura u(xi,t)\n%s %s %s', s1,s2,s3))

end

Замечание. Здесь вычисление функции от матрицы   реализуется с использованием стандартной функции expm(A*t).

Результаты счетадля  , 

ввести s=12

ввести g=3

ввести количество внутренних точек n=7

ввести L=1

ввести alpha=1

 значения функции температуры u(xi, t)

U(0.00): 3.00 7.41 10.88 13.41 15.00 15.66 15.38 14.16 12.00

U(0.01): 3.00 7.03 10.42 12.94 14.53 15.19 14.92 13.78 12.00

U(0.08): 3.00 5.51 7.81 9.71 11.11 11.96 12.31 12.26 12.00

U(0.16): 3.00 4.77 6.44 7.94 9.19 10.19 10.94 11.52 12.00

U(0.23): 3.00 4.43 5.81 7.10 8.29 9.35 10.31 11.18 12.00

U(0.31): 3.00 4.27 5.51 6.72 7.87 8.97 10.01 11.02 12.00

U(0.39): 3.00 4.19 5.37 6.53 7.67 8.78 9.87 10.94 12.00

U(0.47): 3.00 4.16 5.31 6.45 7.58 8.70 9.81 10.91 12.00

U(0.55): 3.00 4.14 5.28 6.41 7.54 8.66 9.78 10.89 12.00

U(0.63): 3.00 4.13 5.26 6.39 7.52 8.64 9.76 10.88 12.00

U(0.70): 3.00 4.13 5.26 6.38 7.51 8.63 9.76 10.88 12.00

U(0.78): 3.00 4.13 5.25 6.38 7.50 8.63 9.75 10.88 12.00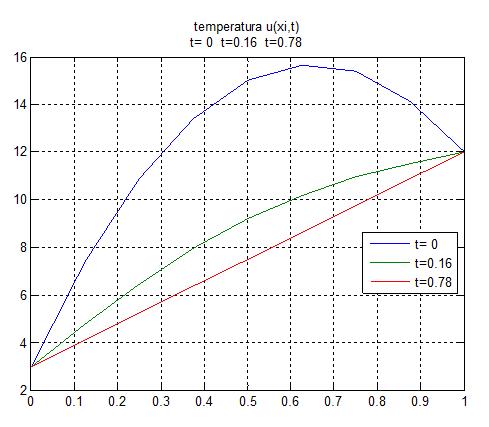

>>



Рис 7.7

Задание

Задача теплопроводности

Вычислить методом конечных разностей по явной схеме распределение температуры по толщине стены в соответствии с задачей, изложенной в теоретической части.

Исходная постановка задачи: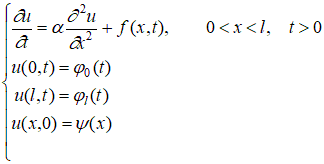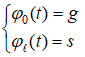



 – функция, характеризующая мощность источника тепла;

 – краевые условия;

 – начальные условия;

 – длина;   – коэффициент температуропроводности;   – предпоследняя цифра в зачетной книжке,   – последняя цифра номера зачетной книжки.

Для обеспечения устойчивости счета принять 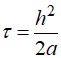 , где h– шаг по оси x, τ-шаг по оси t.

Применить форму счета по явной схеме:

 i=1,…, n-1 k=0,1,2,3,…

1. Решить задачу на ЭВМ для n=10 точек по координате x и k=100 шагов по времени (координата t) .

Представить результаты счета для n=10 и k c распечаткой результатов при следующих k: k=0, 10, 20, 30, . . . , 90, 100

2. Решить задачу вручную для n=4, k=0,1,2.