прикладная математика практикум. Прикладная математика_Практикум. Практическая работа 1 Первичная статистическая обработка экспериментальных данных Пример

• Название: Практическая работа 1 Первичная статистическая обработка экспериментальных данных Пример
• Анкор: прикладная математика практикум
• Дата: 19.09.2022
• Размер: 1.37 Mb.
• Имя файла: Прикладная математика_Практикум.docx
• Тип: Практическая работа; #685223
• страница: 2 из 13

Практическая работа № 2

2. Модель однофакторного дисперсионного анализа

Пример.  В таблице приведены данные по объемам работ, выполненных на стройке за смену для 4-х бригад.

Таблица 2.1

Номер бригады	Объем выполненной работы
1	140	144	142	145
2	150	149	152	152
3	148	149	146	147
4	150	155	154	152

Проверим по критерию Бартлетта гипотезу о равенстве групповых дисперсий. В этой задаче k = 4; n_i = 4, i=1;2;3;4. Объем выборки n=16.

Расчеты по п.1 и п.2 проведем в таблице 2.2.

Таблица 2.2

Расчет дисперсии

Номер бригады (i)	Объем выполненной работы x(i)j				Групповые средние	Групповые дисперсии
1	140	144	142	145	142,75	4,92
2	150	149	152	150	150,25	1,58
3	148	149	146	147	147,50	1,67
4	150	155	154	152	152,75	4,92

3. Общая оценка дисперсии:  .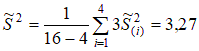

4. Статистика Бартлетта:  .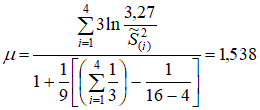

5. Выберем уровень значимости q=0,05 и по таблице распределения χ² с 3 степенями свободы находим критическое значение: μ_кр = χ²_{0,95, 3}=7,82.

Значение статистики меньше критического, следовательно, можно принять гипотезу о равенстве групповых дисперсий.

Продолжим решение задачи о стройке. Проверим гипотезу дисперсионного анализа о равенстве средних.

Таблица 2.3

Номер бригады  (i)	Групповые средние	Групповые дисперсии
1	142,75	4,92
2	150,25	1,58
3	147,50	1,67
4	152,75	4,92

Общее выборочное среднее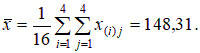 

Межгрупповая дисперсия  .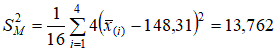

Внутригрупповая дисперсия  .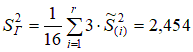

Дисперсионное отношение:  .

По таблицам распределения Фишера – Снедекора для α=0,05 степеней свободы k₁ =3, k₂ =12 найдем критическое значение F_кр=3,49.

Так как дисперсионное отношение больше критического, то гипотезу Н₀ отклоняем и считаем, что объем ежедневной выработки зависит от работающей бригады.

Два последних рассмотренных критерия используют в важном разделе математической статистики – дисперсионном анализе.

Продолжим решение задачи о стройке. Ранее было получено, что объем ежедневной выработки зависит от работающей бригады. Оценим степень этой зависимости с помощью коэффициента детерминации. Было получено, что 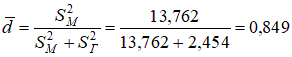 ;  ; следовательно, коэффициент детерминации



Это означает, что 84,9 % общей вариации ежедневного объема выработки связано с работающей сменой.

Оценка математического ожидания (средней выработки на стройке)  m = M(Y)  равна  .

Оценки параметров  соответственно равны:

 



Пример.  Через равные промежутки времени в тонком растворе золота регистрировалось количество частиц золота, попавших в поле зрения микроскопа.

Таблица 2.4

Число частиц	0	1	2	3	4	5	6	7	Всего
Частоты (ni)	112	168	130	68	32	5	1	1	518

Проверить, что количество частиц золота, попавших в поле зрения микроскопа, имеет распределение Пуассона.

Решение.

Распределение Пуассона – это дискретное однопараметрическое распределение, вероятности которого определены формулами: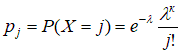

 для 

Сначала оценим параметр распределение Пуассона.



Далее объединим 3 последних столбца таблицы:

Таблица 2.5

Число частиц	0	1	2	3	4	5 и более	Всего
Частоты (ni)	112	168	130	68	32	7	518

Теперь вычислим оценки для теоретических вероятностей: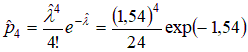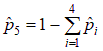

;  ;

;  .

Количество степеней свободы: k – 2=6–2=4.

Значение статистики критерия: χ²(4)=7,85.

Критическое значение найдем по таблице 3 приложения: χ²_кр =9,49.

Согласие имеет место.

Проверка гипотезы о том, что генеральное распределение – нормальное.

Нормально распределенная случайная величина Х имеет плотность распределения: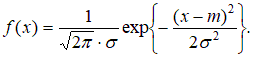



Эта плотность зависит от 2-х параметров:

m – математическое ожидание случайной величины Х и

σ² – дисперсия случайной величины Х .

Оценки параметров нормального распределения: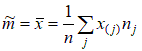

 – выборочное среднее;

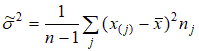– «подправленная» выборочная дисперсия.

Здесь  – середина j-го интервала группировки n_j – число элементов выборки, попавших в j-го интервала группировки.

Теоретическая вероятность попадания в j-ый интервал группировки

p_j=P {XÎΔ_j |H₀ } . 

В частности, если произведено разбиение на одинаковые по длине интервалы 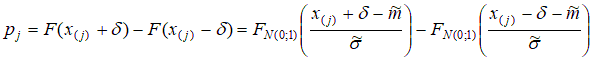  длины 2δ, то



Здесь F_N(0;1) – функция распределения стандартно нормального закона 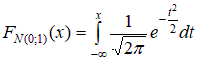  (её значения находят по соответствующим таблицам).

Для того чтобы упростить вычисления, можно пользоваться приближенной формулой: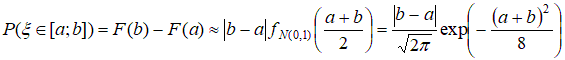



где ξ – случайная величина, имеющая стандартно нормальное распределение.

Применяя данную формулу получаем, что теоретическую вероятность попадания в j-ый интервал группировки 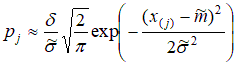 можно вычислить без применения таблиц значений функции распределения стандартно нормального закона:



Если гипотеза о том, что распределение генеральной случайной величины является нормальным, проверяется с помощью критерия Пирсона, то статистика критерия имеет вид: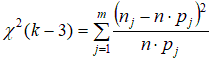



Пример. Имеются следующие данные распределения 200 проб нити по крепости:

Таблица 2.6

Крепость нити	120 – 130	130– 140	140– 150	150– 160	160– 170	170– 180	180– 190	190– 200
число проб	1	8	27	58	56	34	14	2

Проверим гипотезу о том, что крепость нити – нормально распределенная случайная величина.

Сначала оценим параметры распределения: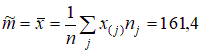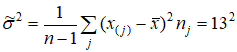

  .

Дальнейшие вычисления представим в виде таблицы:

Таблица 2.7

Крепость нити	120 – 130	130– 140	140– 150	150– 160	160– 170	170– 180	180– 190	190– 200
nj	1	8	27	58	56	34	14	2
	–2,80	–2,03	–1,26	–0,49	0,28	1,05	1,82	2,58
n∙pj	1	8	28	55	59	35	12	2

Здесь  – середина j-го интервала группировки n_j – число элементов выборки, попавших в j-го интервала группировки, вероятности попадания в j-й интервал группировки рассчитывалась по формуле



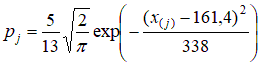Как видно из таблицы, теоретические частоты близки к эмпирическим, хотя отдельные расхождения имеют место. Для случайности или существенности этих расхождений используем критерии согласия.

Статистика критерия Пирсона  .

Критическое значение найдем по таблице 3 приложения χ²_0,95;5= 11,7.

Значение статистики значительно меньше критического, согласие хорошее.