Практикум по коллоидной химии Электроповерхностные свойства и устойчивость дисперсных систем

• Название: Практикум по коллоидной химии Электроповерхностные свойства и устойчивость дисперсных систем
• Дата: 24.05.2022
• Размер: 346.5 Kb.
• Имя файла: Prakt_Ch_3_3__1.doc
• Тип: Практикум; #546801
• страница: 5 из 7

Цель работы

1. Изучение зависимости вязкости от концентрации раствора полимера и сопоставление с уравнением Эйнштейна; 2. Исследование зависимости вязкости от концентрации раствора и вычисление молекулярной массы полимера.

Теоретическая часть

Разбавленные агрегативно устойчивые дисперсные системы не образуют пространственной сетки из частиц дисперсной фазы (структуры), и поэтому их реологические свойства близки или подобны свойствам дисперсионной среды. Зависимость вязкости таких систем от концентрации дисперсной фазы описывается уравнением Энштейна:

=₀(1+) или _уд(-₀)₀=

где ₀ – вязкость дисперсионной среды;  - объемная доля дисперсной фазы;  - коэффициент формы частиц (для сферических частиц = 2,5); _уд – удельная вязкость.

С увеличением концентрации дисперсной фазы возрастает взаимодействие между частицами и обнаруживаются все более сильные отклонения от уравнения Энштейна. Вязкость концентрированных систем растет с концентрацией почти по экспоненте.

Зависимость удельной вязкости не слишком концентрированных растворов полимеров от концентрации обычно удовлетворительно описывается уравнением, предложенным Хаггинсом:

_уд/с = k₁²c (2.9)

где  -характеристическая вязкость; с – концентрация раствора, г/100мл; k₁ – коэффициент, называемый константой Хаггинса.

Коэффициент k₁ сужит характеристикой взаимодействия макромолекул в системе полимер – растворитель. Его значение практически не зависит от молекулярной массы полимера и меняется лишь в зависимости от природы растворителя. В хороших растворителях значения константы Хаггинса составляет 0,2-0,3.

Характеристическая вязкость, отражающая гидродинамическое сопротивление молекул полимера потоку жидкости, может быть определена для разбавленных растворов, в которых взаимодействие макромолекул между собой настолько мало, что им можно пренебречь. Для нахождения характеристической вязкости устанавливают зависимость вязкости от концентрации в довольно узком интервале низких концентраций и полученные результаты экстраполируют к нулевой концентрации.

Характеристическую вязкость можно вычислить также и путем экстрополяции зависимости логарифмической приведенной вязкости ln_отн/с от концентрации. Разложение функции ln _отн/с в ряд по степеням _отн/с приводит к выражению

ln_отн/с=ln(1+_уд)/с=_уд/с-(_уд/с)²*с/2+(_уд/с)³с²/3-… (2.10)

Следовательно:

lim_c(ln_отн/c) = lim_c(_уд/c)= (2.11)

С учетом лишь двух первых членов ряда уравнение (2.10) принимает вид

ln_отн/c=-k₂²c (2.12)

Экстраполяция по этому уравнению считается более точной, чем экстраполяция по уравнению Хаггинса, поскольку в большинстве случаев постоянная уравнения (2.12) k₂k₁. Было показано, что постоянные уравнений (2.9) и (2.12) с хорошим приближением удовлетворяют зависимости:

k₂₊k₁=0,5 (2.13)

Характеристическая вязкость непосредственно зависит от молекулярного веса полимера, причем она тем больше, чем выше молекулярный вес М. Связь между  и М обычно удовлетворительно выражается эмпирическим уравнением Марка – Куна:

=kM^а (2.14)

где k и а – константы, характерные для исследуемого раствора в данном растворителе.

Константы k и а для каждой системы полимер – растворитель находят эмпирически, путем подстановки в уравнение (2.14) найденного значения  и молекулярной массы, определенной одним из абсолютных методов (например, методом светорассеяния).

Теоретические расчеты показывают, что константа а для растворов полимеров в плохих растворителях равна 0,5. В хороших растворителях значение а повышается и может достигать 0,8.

Таблица 2.4. Обозначение и названия величин, принятые в вискозиметрии растворов полимеров

Обозначение величиныОбычное названиеРекомендуемое название_отн₀
_уд=_отн-1=(-₀)/ ₀

_пр=_уд/с

ln _отн/с
=(_уд/с)_с=(ln_отн/с)_с

Относительная вязкость

Удельная вязкость

Приведенная вязкость

Логарифмическая приведенная
Характеристическая вязкостьОтношение вязкостей
Удельная вязкость

Число вязкости

Логарифмическое число вязкости
Предельное число вязкости

В связи с тем, что терминология, используемая в вискозиметрии растворов полимеров, в последнее время претерпевала изменения, в табл. 2.4 приведены названия величин и их обозначения, принятые в вискозиметрии растворов полимеров. Во втором столбце этой таблицы дано обычно употребляемое название вязкости, а в третьем – названия, рекомендованные Международным союзом теоретической и прикладной химии.

Следует отметить, что полученное по уравнению (2.14) значение молекулярной массы является среднестатистическим, поскольку любой реальный полимер представляет собой полидисперсную смесь макромолекул.

Значения средневязкостной молекулярной массы зависят от характера связи между  и М и лежат ближе к значениям средневесовой, а не среднечисленной молекулярной массы. Поэтому при выборе констант k и a для расчета средневязкостной молекулярной массы лучше пользоваться данными, полученными методом светорассеяния, а не осмометрии, по которой определяется среднечисленная молекулярная масса. Это уменьшает ошибки при расчете и позволяет получить более достоверные значения молекулярной массы. При определении молекулярного веса необходимо обращать внимание на то, чтобы полученное значение находилось в пределах того диапазона значений молекулярной массы, для вычисления которого империческое уравнение (2.14) применимо с достаточной точностью.

В табл. 2.5 приведены значения констант k и а для некоторых полимеров.

Определение вязкости растворов полимеров основано на измерении времени истечения жидкостей из капилляра вискозиметра. Расчет проводят по уравнению Пуазейля уравнение (V.6).

Если жидкость протекает через капилляр под действием собственного веса, то

p=gh (2.15)
где  - плотность раствора; g – ускорение силы тяжести; h – средняя высота столба жидкости, создающего гидростатическое давление р.

Подставляя значение р в уравнение Пуазейля и решая его относительно , можно получить

r⁴gh/8Vl (2.16)

Таблица 2.5. Константы k и а в уравнении Марка - Куна

ПолимерРастворительТем-ра растворенияk*10⁴аДиапазон молекулярных весов, М*10^-3Полиэтилен

Полипропилен

Полиизобутилен

Полибутодиен

Бутилкаучук

Полистирол

Поливиниловый спирт

Полиакриламид

ПолиметилметакрилатДекалин

Декалин

Толуол

Бензол

Бензол

Циклогексан

Вода
Вода
Элилацетат100

135

25

32

25

34

25
25
3510,5

1,0

8,7

1,0

69

8,2

5,95
0,63
4,790,63

0,80

0,56

0,77

0,50

0,50

0,63
0,80
0,6023-35

100-1100

110-340

143-1640

1,1-500

4,7-6270

11,6-195
10-5000

3

8,1-455

При использовании одного и того же вискозиметра и при работе с одним и тем же объемом жидкости можно написать

с (2.17)

где с – константа вискозиметра.

Отсюда, зная константу прибора и время истечения жидкости из капилляра, можно вычислить вязкость жидкости. Однако обычно при измерении вязкости растворов достаточно определить относительную вязкость раствора _отн – отношение вязкости раствора  к вязкости растворителя ₀:

_отн=/₀=₀₀ (2.18)

где ₀ – плотность растворителя; ₀ – время истечения растворителя.

Для разбавленных растворов можно допустить, что плотность раствора близка к плотности растворителя и тогда

_отн₀ (2.19)

Необходимым условием использования уравнения Пуазейля для расчета вязкости является ламинарность движения жидкости в капилляре. Турбулентности потока избегают путем соответствующего подбора диаметра и длины капилляра вискозиметра. В вискозиметрах, условия течения жидкости в капилляре при обычных перепадах давления соответствуют числам Рейнольдса, меньшим 200. Отклонения от закона Пуазейля возможны также вследствие того, что, строго говоря, растворы полимеров представляют собой неньютоновские жидкости, вязкость которых зависит от скорости их истечения через капилляр. Для того чтобы свести к минимуму этот источник ошибок, для измерений вязкости растворов полимеров принято использовать вискозиметры, время истечения жидкости, в которых достаточно велико и составляет 100-200 с. Для определения вязкости растворов полимеров обычно применяют капиллярные вискозиметры типа вискозиметра Оствальда или вискозиметра Уббелоде (рис. 2.6).

При истечении раствора в вискозиметре Оствальда происходит постепенное уменьшение высоты столба жидкости h, что приводит к созданию переменного гидростатического давления р. Поэтому в вискозиметр Оствальда всегда наливают одно и тоже количество раство ра.

В вискозиметре Уббелоде поток жидкости прерывается в конце капилляра, и поэтому давление столба жидкости, под которым происходит ее течение, не зависит от объема жидкости, заливаемой в вискозиметр. Вискозиметры такого типа называются вискозиметрами с висячим уровнем. Их основным преимуществом является то, что разбавление растворов можно осуществлять непосредственно в вискозиметре.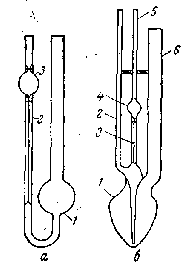



Рис. 2.6. Вискозиметры Оствальда (а) и Уббелоде (б)

Методика проведения работы

Для проведения работы необходимы:

Вискозиметр Оствальда (для первого варианта работы) или вискозиметр Уббелоде с висячим уровнем (для второго варианта работы).

Термостат.

Пипетки емкостью 5 и 20 мл.

Растворы полимера (четыре – для первого варианта работы и один – для второго варианта).

Растворитель.
Определения вязкости растворов вискозиметром Оствальда

В тщательно вымытый вискозиметр (см. рис. 2.6а) наливают определенный объем растворителя до метки, нанесенной на нижнем шарике 1. Помещают вискозиметр в термостат так, чтобы капилляр 2 и верхний шарик 3 были полностью погружены в термостатирующую жидкость. Выдерживают вискозиметр в термостате 10 минут, после чего приступают к измерениям. С помощью груши засасывают растворитель в верхний шарик 3 выше верхней метки и определяют время истечения растворителя от верхней метки шарика до нижней. Определение времени истечения проводят не менее трех раз и берут среднее из полученных значений. Вынимают вискозиметр из термостата, выливают растворитель и заполняют вискозиметр раствором полимера наименьшей концентрации. После 10 мин термостатирования определяют время истечения данного раствора. Подобным образом определяют время истечения всех остальных растворов полимера в порядке возрастания концентрации. В конце работы тщательно промывают прибор и повторно определяют время истечения растворителя.

Рассчитывают значения _отн и  и полученные данные записывают в таблицу (см. табл.2.6).

Определение вязкости растворов вискозиметром Уббелоде.

Тщательно вымытый и просушенный вискозиметр (см.рис.2.6в) помещают в термостат, в котором поддерживается строго постоянная заданная температура. При этом необходимо следить за тем, чтобы капилляр 3 и шарик вискозиметра 4 были полностью погружены в термостатирующую жидкость.

Таблица 2.6. Форма записи данных, полученных при измерении вязкости растворов полимера

Концентрация раствора

полимера с, г/100млВремя истечения, , с_отн, сП_уд^*_уд^*/с(ln_отн^*)/c

Работу начинают с определения вязкости раствора полимера. В колено 6 с помощью пипетки наливают 5 мл исходного раствора. После 10-15 мин термостатирования при помощи груши с резиновой трубкой, надетой на колено 5 вискозиметра, засасывают раствор в шарик вискозиметра чуть выше верхней метки.

При этом колено 2 должно быть закрыто с помощью зажима на резиновой трубке, надетой на конец колена. Затем приоткрывают зажим и определяют время истечения раствора из шарика 4. в резервуар 1. В момент прохождения жидкостью верхней метки включают секундомер и измеряют время, необходимое для истечения жидкости от верхней метки измерительного шарика до нижней. Определение времени истечения жидкости проводят таким образом не менее трех раз и вычисляют среднее значение из трех измерений. После этого раствор полимера разбавляют непосредственно в вискозиметре, добавляя с помощью пипетки точно измеренное количество растворителя, и определяют время истечения разбавленного раствора. Разбавление растворов проводят последовательно несколько раз таким образом, чтобы концентрация каждого последующего раствора была в два раза меньше концентрации предыдущего. Рассчитывают концентрации исследуемых растворов в г/100мл.

После каждого разбавления измеряют время истечения полученных растворов таким же образом, как это было описано для исходного раствора. По окончании работы с растворами полимера вискозиметр промывают несколько раз растворителем, засасывая его каждый раз в капилляр 3 и шарик 4. Затем промывную жидкость выливают из вискозиметра, наливают в него 5 мл чистого растворителя и определяют время истечения растворителя. Средние значения времени истечения растворов и растворителя записывают в таблицу (см.табл.2.6). Рассчитывают значения удельной, приведенной и логарифмической приведенной вязкости и также записывают полученные данные в таблицу. Строят графики зависимости величин _уд/с и ln_отн/с от концентрации раствора с (рис.V.7) и экстраполируют полученные прямые к нулевой концентрации. Отсекаемые на оси ординат отрезки дают значения характеристической вязкости . В случае, если прямые не пересекаются в одной точке, определяют среднее значение характеристической вязкости. По тангенсу угла наклона прямых определяют значения константы Хаггинса k₁ и константы k₂ уравнения (2.12).

Согласно рис. V.7 и уравнений 2.9 и 2.12 k₁=tg ² и k₂=tg ².Значения тангенсов рассчитывают как отношение сторон соответствующих треугольников с учетом масштаба, выбранного для построения графиков.

Полученное значение характеристической вязкости, а также значения констант k и а, взятые из табл.2.5, подставляют в уравнение Марка–Куна (2.14) и рассчитывают молекулярную массу исходного полимера.

РАБОТА 7

ИССЛЕДОВАНИЕ КИНЕТИКИ ОГРАНИЧЕННОГО НАБУХАНИЯ ПОЛИМЕРА

Цель работы

Исследование кинетики ограниченного набухания ненаполненной резины и нахождение константы скорости набухания и числа набухания объемным методом.