лабараторна 9. Практикум (раздел 3) Введение
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
Приложение 3. Использование возможностей пакета Matrixer 5.1 для проведения корреляционного и регрессионного анализаПрограмма предназначена для анализа и обработки данных, проведения эконометрических и статистических расчетов. Основной тип объектов – матрицы (вектор рассматривается как одномерная матрица). Имеется возможность обмена данными с электронными таблицами Excel. Главное окно программы имеет вид 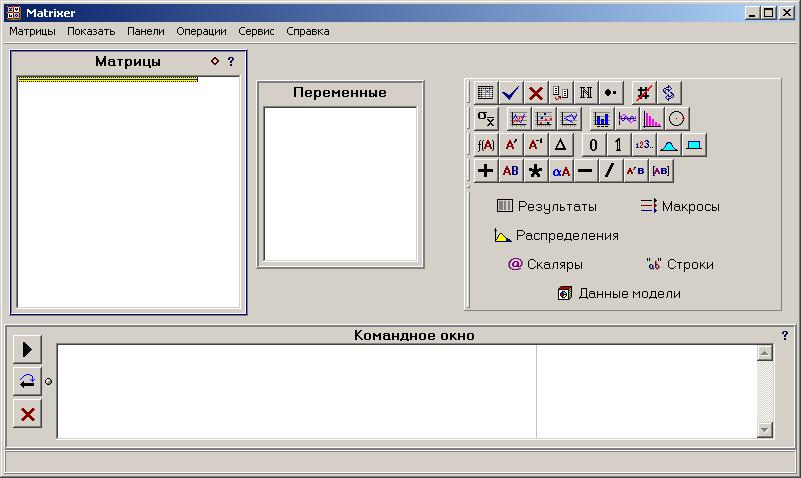 Рис. П3.1. Главное окно программы Matrixer 5.1 3.1. Корреляционный анализ Рассмотрим построение корреляционной матрицы (матрицы парных корреляций) 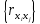 по данным наблюдений за совместным изменением n переменных по данным наблюдений за совместным изменением n переменных 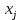 (табл. 3.1). (табл. 3.1).Создадим новый объект – матрицу X, столбцами которой являются столбцы данных наблюдений. Для этого вызовем пункт меню «Матрицы. Создать» либо нажмем кнопку 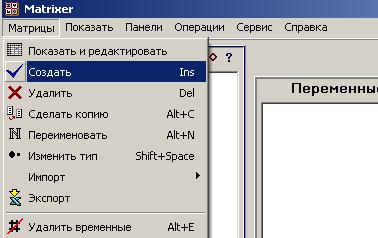 Рис. П3.2. Вызов пункта меню «Матрицы. Создать» После задания имени (X) объекту на экране появится окно ввода данных (рис. П3.3)  Рис. П3.4. Окно ввода данных Ввод данных можно осуществлять с клавиатуры либо использовать копирование табличных данных через буфер обмена. После ввода данных окно данных матрицы X принимает вид 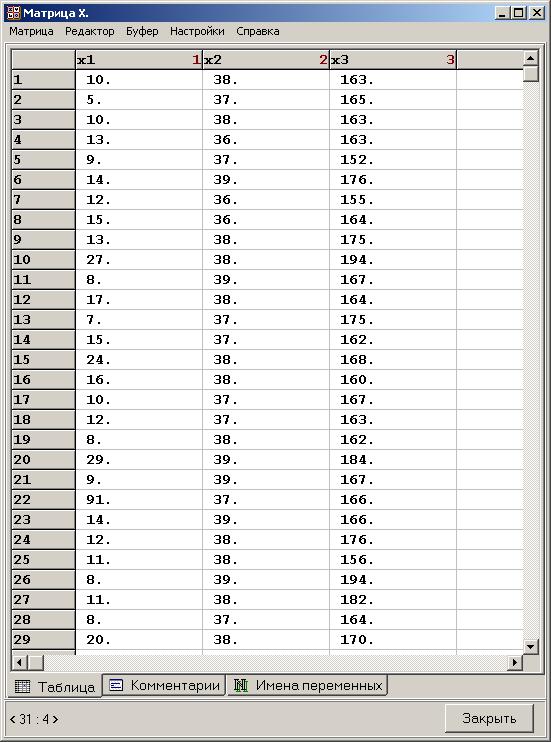 Рис. П3.5. Окно данных матрицы X Далее для получения корреляционной матрицы необходимо набрать формулу «corr! X» в Командном окне (рис. П3.6) и нажать кнопку  Рис. П3.6. Командное окно программы Matrixer 5.1 Результат будет иметь вид 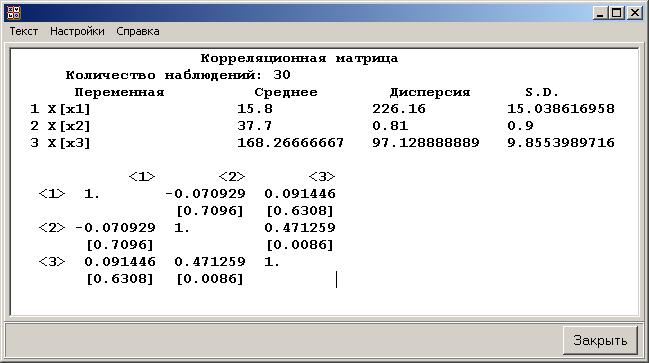 Рис. П3.7. Окно результатов регрессионного анализа Числа в квадратных скобках означают стандартные ошибки определения соответствующего коэффициента корреляции, т. е. корреляционная матрица имеет вид
Рис. П3.8. Корреляционная матрица 3.2. Регрессионный анализ Рассмотрим построение уравнения линейной множественной регрессии по данным наблюдений за совместным изменением p+1 переменной y и 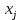 и (( и ((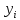 , , 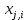 ); j = 1, 2, ..., p; i = 1, 2, ..., n) (табл. 3.1). ); j = 1, 2, ..., p; i = 1, 2, ..., n) (табл. 3.1).Создадим новый вектор Y, как было показано в предыдущем пункте со значениями, показанными на рис. П2.1. Для построения уравнения линейной множественной регрессии необходимо набрать формулу «Y: 1 X» в Командном окне (рис. П3.9) и нажать кнопку 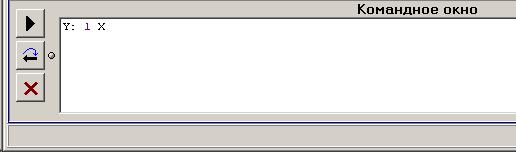 Рис. П3.9. Командное окно программы Matrixer 5.1 Результат будет иметь вид 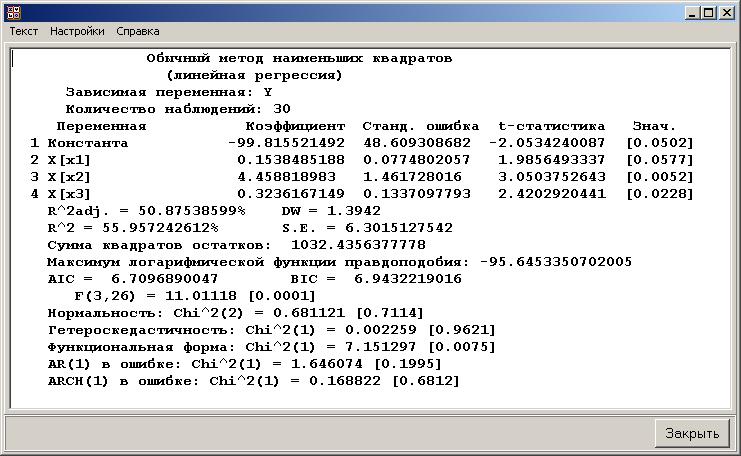 Рис. П3.10. Окно результатов построения корреляционной матрицы Искомые значения коэффициентов линейного уравнения регрессии (a, 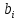 ) берутся из столбца «Коэффициенты» таблицы результатов регрессии, из которой следует, что уравнение регрессии имеет вид ) берутся из столбца «Коэффициенты» таблицы результатов регрессии, из которой следует, что уравнение регрессии имеет вид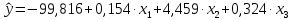 . .Столбец «Станд. ошибка» содержит стандартные ошибки определения коэффициентов уравнения регрессии. Столбец «t-статистика» содержит фактические значения критерия Стьюдента для соответствующего коэффициента. Столбец «Знач.» содержит минимальный уровень значимости коэффициента 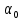 . .Коэффициент детерминации 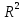 = 0,55957. = 0,55957.Модифицированный коэффициент детерминации (У3.28) 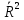 = 0,50875. = 0,50875. |
