лабараторна 9. Практикум (раздел 3) Введение
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
Приложение 2. Использование возможностей MS Excel для проведения корреляционного и регрессионного анализаКорреляционный анализ Рассмотрим построение корреляционной матрицы (матрицы парных корреляций) 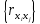 по данным наблюдений за совместным изменением n переменных по данным наблюдений за совместным изменением n переменных 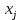 (табл. 3.1). (табл. 3.1).Расположим исходные данные в ячейках с С4 по F33 (рис. П2.1) и вызовем функцию «Сервис. Анализ данных. Корреляция» табличного процессора MS Excel (рис. П2.1, П2.2). 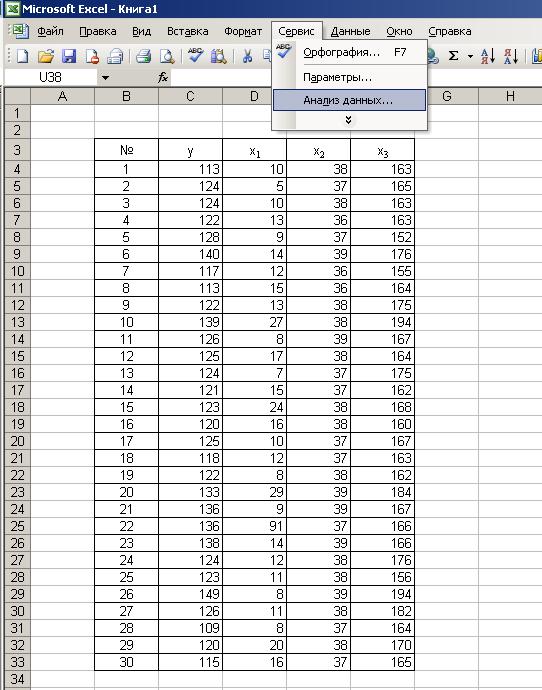 Рис. П2.1. Вызов функции «Сервис. Анализ данных» 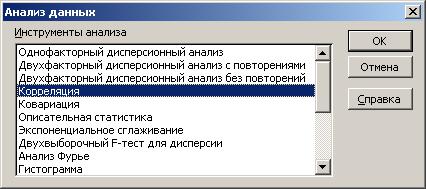 Рис. П2.2. Вызов функции «Сервис. Анализ данных. Корреляция» окне ввода параметров функции «Сервис. Анализ данных. Корреляция» (рис. П2.3) необходимо указать диапазон ячеек, содержащих исходные данные («Входной интервал»), и диапазон ячеек, в которых будет располагаться полученная корреляционная матрица («Выходной интервал»). 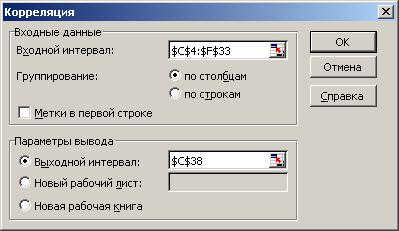 Рис. П2.3. Окно ввода параметров функции «Сервис. Анализ данных. Корреляция» области ячеек, начиная с указанной ячейки С38 получим искомую матрицу (рис. П2.4):
Рис. П2.4. Корреляционная матрица Регрессионный анализ Рассмотрим построение уравнения линейной множественной регрессии по данным наблюдений за совместным изменением p+1 переменной y и 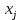 и (( и ((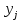 , ,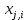 ); j=1, 2, ..., p; i=1, 2, ..., n) (табл. 3.1). ); j=1, 2, ..., p; i=1, 2, ..., n) (табл. 3.1).Будем считать, что имеется три факторные переменные (p = 3) и число наблюдений равно 30. Расположим исходные данные в ячейках с С4 по F33 и вызовем функцию «Сервис. Анализ данных. Регрессия» табличного процессора MS Excel (рис.П2.1, П2.5), в результате чего на экране появится окно ввода параметров данной функции (рис. П2.6).  Рис. П2.5. Вызов функции «Сервис. Анализ данных. Регрессия» окне ввода параметров функции «Сервис. Анализ данных. Регрессия» (рис. П2.6) необходимо указать диапазон ячеек, содержащих исходные данные («Входной интервал по Y», «Входной интервал по X»), и место, где будут рас-полагаться результаты: диапазон ячеек на данном рабочем листе, новый рабочий лист, новая рабочая книга («Выходной интервал»). Если требуется получить уравнение регрессии без свободного члена, то нужно установить флажок «Константа–ноль» (рис. П2.6);  Рис. П2.6. Окно ввода параметров функции «Сервис. Анализ данных. Регрессия» После выполнения функции «Сервис. Анализ данных. Регрессия» рабочий лист Excel примет вид (рис. П2.7). 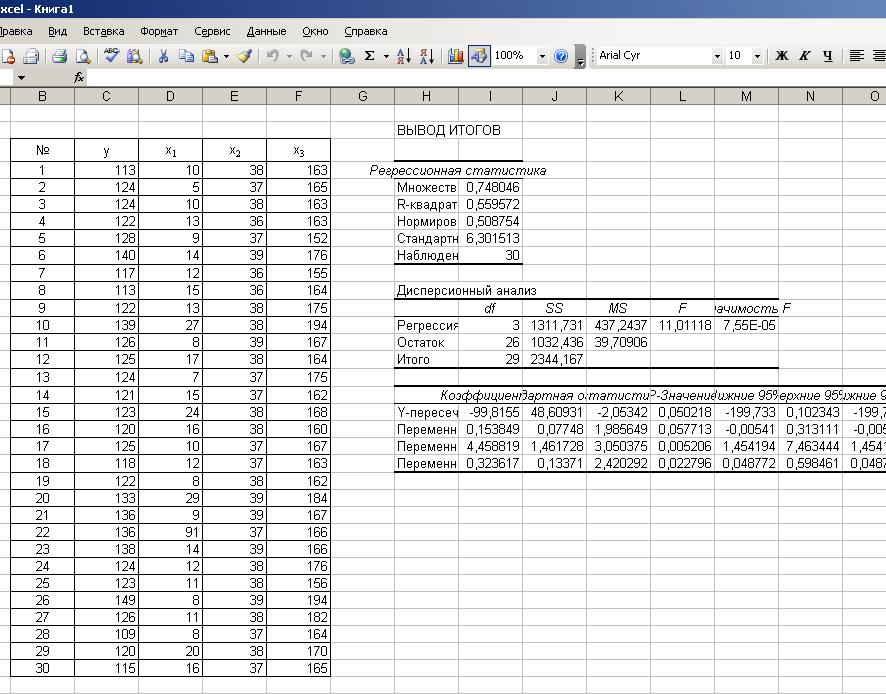 Рис. П2.7. Результаты регрессионного анализа – вызова функции «Сервис. Анализ данных. Регрессия» Результаты регрессионного анализа представлены в виде трех таблиц Таблица П2.1 Результаты корреляционного анализа («Регрессионная статистика»)
Множественный коэффициент корреляции R Коэффициент детерминации 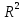 Модифицированный коэффициент Модифицированный коэффициентдетерминации 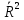 (У3.28) (У3.28) Стандартная ошибка определения R Число наблюдений Таблица П2.2 Результаты дисперсионного анализа
Столбец «Сумма квадратов отклонений» содержит следующие суммы: Регрессия = 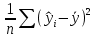 ; Остаток = ; Остаток = 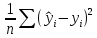 ; Итог= ; Итог= 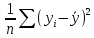 . .Столбцы «Статистика Фишера F» и «Уровень значимости» содержат фактическое значение критерия Фишера F = 11,011 и минимальный уровень значимости уравнения регрессии 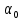 , т. е. уравнение регрессии значимо при всех α > , т. е. уравнение регрессии значимо при всех α > 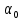 . .Таблица П2.3
Искомые значения коэффициентов линейного уравнения регрессии (a, 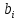 ) берутся из столбца «Коэффициенты» таблицы результатов регрессии (табл. 2.3), из которой следует, что уравнение регрессии имеет вид ) берутся из столбца «Коэффициенты» таблицы результатов регрессии (табл. 2.3), из которой следует, что уравнение регрессии имеет вид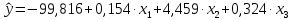 . .Столбец «Стандартная ошибка определения коэффициентов» содержит стандартные ошибки определения коэффициентов уравнения регрессии. Столбец «t-статистика» содержит фактические значения критерия Стьюдента для соответствующего коэффициента. Столбец «Вероятность ошибки» содержит минимальный уровень значимости коэффициента 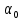 . .Столбцы «Нижние 95%–пределы» и «Верхние 95%–пределы» содержат границы доверительных интервалов для значений коэффициентов. Разные знаки нижней и верхней границы доверительного интервала говорят о ненадежности полученного значения соответствующего коэффициента (свободный член и первый коэффициент в нашем примере). |
