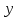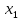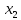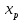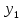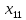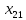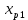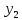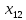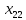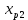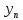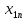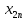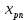лабараторна 9. Практикум (раздел 3) Введение
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
3.1. Понятие множественной регрессииМножественная регрессия представляет собой уравнение связи с несколькими независимыми переменными: 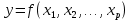 где y – зависимая переменная (результативный признак); 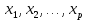 – независимые переменные (факторы). – независимые переменные (факторы).Множественная регрессия применяется в ситуациях, когда из множества факторов, влияющих на результативный признак, нельзя выделить один доминирующий фактор и необходимо учитывать влияние нескольких факторов. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель. Постановка задачи множественной регрессии. По имеющимся данным n наблюдений за совместным изменением 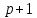 переменной y и переменной y и 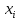 и и 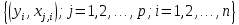 (табл. 3.1) необходимо определить аналитическую зависимость (табл. 3.1) необходимо определить аналитическую зависимость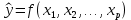 , наилучшим образом описывающую данные наблюдений , наилучшим образом описывающую данные наблюдений Таблица 3.1 Результаты наблюдений
Как и в случае парной регрессии, построение уравнения множественной регрессии осуществляется в два этапа: спецификация модели; оценка параметров выбранной модели. Спецификация модели включает в себя решение двух задач: отбор p факторов 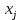 , наиболее влияющих на величину y; , наиболее влияющих на величину y;выбор вида уравнения регрессии 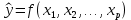 ;. ;. |