лабараторна 9. Практикум (раздел 3) Введение
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
Контрольные вопросыЧто понимается под множественной регрессией? Какие задачи решаются при построении уравнения регрессии? Какие задачи решаются при спецификации модели? Какие требования предъявляют к факторам, включаемым в уравнении регрессии? Что понимается под коллинеарностью факторов? Как проверяется наличие коллинеарность? Какие подходы применяются для преодоления межфакторной корреляции? Какие функции чаще используются для построения уравнения множественной регрессии? По какой формуле вычисляется индекс множественной корреляции? Как вычисляются индекс множественной детерминации? Что означает низкое значение коэффициента множественной корреляции? Как проверяется значимость уравнения регрессии и отдельных коэффициентов? Как строятся частные уравнения регрессии? Как вычисляются средние частные коэффициенты эластичности? Что понимается под гомоскедастичностью ряда остатков? Как проверяется гипотеза о гомоскедастичности ряда остатков? Задачи 1. Проверить наличие линейной коллинеарности между факторами x, z, t, если корреляционная матрица имеет вид
Коллинеарны z и t). 2. Дать интерпретацию параметрам уравнения регрессии 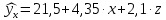 . .(При увеличении x на 1 величина ŷxизменится на 4,35, а при увеличении z на 1 – на 2,1). 3. Дать интерпретацию параметрам уравнения регрессии 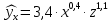 . .(При увеличении x на 1% величина 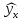 изменится на 0,4%, а при увеличении z на 1% – на 1,1%). изменится на 0,4%, а при увеличении z на 1% – на 1,1%).4. По заданному уравнению регрессии 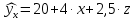 . .построить частные уравнения регрессии, если 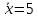 , , 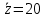 . .( 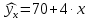 , , 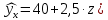 . .5. По заданному уравнению регрессии 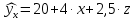 . .найти коэффициенты эластичности, если 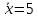 , , 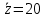 , , 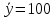 . (0,2; 0,5). . (0,2; 0,5).6. По величине коэффициента детерминации R2 = 0,45 определить долю вариации результативного признака, объясненного уравнением регрессии. (45%) 7. Из предложенных уравнений выбрать лучшее 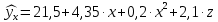 , R2 = 0,456, , R2 = 0,456,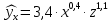 , R2 = 0,56. , R2 = 0,56.(Второе). 8. Найти критические значения F–критерия и t–критерия по количеству наблюдений и уровню значимости: n = 50, α = 0,01, m = 2; n = 20, α = 0,05, m = 3, где m – количество факторов в уравнении регрессии. (5,09; 2,81). 9. По величине множественного коэффициента корреляции rxy = 0,56 для уравнения регрессии 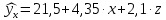 , ,проверить его значимость (α = 0,05). Число наблюдений n = 25. (Значимо). |
