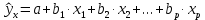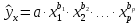лабараторна 9. Практикум (раздел 3) Введение
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
3.2. Отбор факторов при построении множественной регрессииВключение в уравнение множественной регрессии того или иного набора факторов связано, прежде всего, с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям: 1. Факторы не должны быть взаимно коррелированы и, тем более, находиться в точной функциональной связи. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель, и параметры уравнения регрессии оказываются неинтепретируемыми. 2. Включаемые во множественную регрессию факторы должны существенно влиять на вариацию независимой переменной. Т. е. включаемые в модель факторы должны быть статистически значимыми и существенно улучшать показатель качества модели (например, коэффициент детерминации 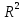 ). ).Отбор факторов производится на основе качественного теоретико-экономического анализа и обычно осуществляется в две стадии: - на первой стадии факторы подбираются исходя из сущности проблемы; - на второй стадии применяются формальные статистические критерии, например, значения t-статистики для соответствующих коэффициентов регрессии. Наличие высокой корреляции выявляется по значению линейного коэффициента 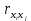 . Если выполняется условие . Если выполняется условие
то факторные переменные 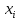 и и 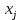 находятся в линейной зависимости между собой, а сами переменные находятся в линейной зависимости между собой, а сами переменные 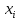 и и 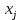 называются явно коллинеарными. называются явно коллинеарными.Значения линейный коэффициентов корреляции 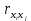 для всевозможных комбинаций переменных для всевозможных комбинаций переменных 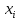 и и 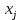 составляют корреляционную матрицу составляют корреляционную матрицу 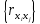 . Для трех факторов матрица . Для трех факторов матрица 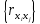 принимает вид принимает вид 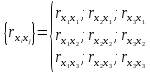 В уравнение регрессии включается только один из коллинеарных факторов, при этом предпочтение отдается тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. Для преодоления сильной межфакторной корреляции используется ряд подходов: - исключение из модели одного или нескольких факторов; - преобразование факторов, при котором уменьшается корреляция между ними; - переход к совмещенным уравнениям регрессии, т. е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие, например 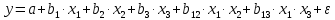 , где члены , где члены 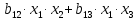 выражают взаимодействие факторов. выражают взаимодействие факторов.После исключения коллинеарных факторов осуществляется процедура отбора факторов, наиболее влияющих на изменение результативного признака (факторов, включаемых в регрессию). Наиболее широкое применение получили: - метод исключения; - метод включения. В уравнении регрессии включаются только значимые факторы, что проверяется с помощью критерия Стьюдента. При отборе факторов рекомендуется, кроме всего прочего, пользоваться следующим правилом: число включаемых факторов должно быть в 6–7 раз меньше объема совокупности, по которой строится регрессия. 3.3. Выбор формы уравнения регрессииКроме точности модели для исследователя наиболее важными качествами модели являются простота модели и возможность наглядной интерпретации параметров модели. По этой причине наиболее широко используются линейная и степенная модели. В уравнении линейной множественной регрессии
параметры 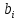 при при 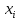 называются коэффициентами «чисто» регрессии и интерпретируется следующим образом. Параметры называются коэффициентами «чисто» регрессии и интерпретируется следующим образом. Параметры 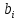 характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне. характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.В уравнении степенной множественной регрессии
показатели степеней 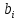 являются коэффициентами эластичности. Они показывают, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1% при неизменности действия других факторов. Этот вид уравнения регрессии получил наибольшее распространение в производственных функциях, в исследованиях спроса и потребления. являются коэффициентами эластичности. Они показывают, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1% при неизменности действия других факторов. Этот вид уравнения регрессии получил наибольшее распространение в производственных функциях, в исследованиях спроса и потребления. |