лабараторна 9. Практикум (раздел 3) Введение
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
Пример выполнения лабораторной работы №3Исходные данные: – данные наблюдений переменных y и x1, x2, x3 даны в таблицы 3.3; – уровень значимости α = 0,05. Таблица 3.3 Исходные данные для примера выполнения лабораторной работы №3
1) Проверка факторов на наличие коллинеарности (п. 3.2). Отбор неколлинеарных факторов. Построим корреляционную матрицу, используя функцию «Сервис.Анализ данных.Корреляция» табличного процессора MS Excel (приложение 2).
Рис. 3.1 Корреляционная матрица Из матрицы следует, что 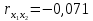 , , 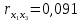 , , 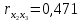 , следовательно, коллинеарность между факторами отсутствует и нет основания исключать какой-либо фактор из рассмотрения. , следовательно, коллинеарность между факторами отсутствует и нет основания исключать какой-либо фактор из рассмотрения.Таким образом, далее будет строиться регрессия y по факторам x1, x2 и x3. 2) Построение уравнения линейной множественной регрессии. Для построения уравнения линейной регрессии используем функцию «Сервис.Анализ данных.Регрессия» табличного процессора MS Excel (рис 3.2): 1) вызов функции осуществляется через пункты меню: <Сервис> – <Анализ данных> – <Регрессия>; 2) указываются ячейки, содержащие исходные значения переменных y и xi (рис. 3.2); 3) если отсутствует свободный член в уравнении регрессии – установить флажок «Константа–ноль» (рис. 3.2); 4) указать место, где будут представлены результаты работы функции (выходной интервал на данном рабочем листе, новый рабочий лист, новая рабочая книга); 5) искомые значения коэффициентов линейного уравнения регрессии (a, bi) берутся из столбца «Коэффициенты» таблицы результатов регрессии (табл. 3.6). 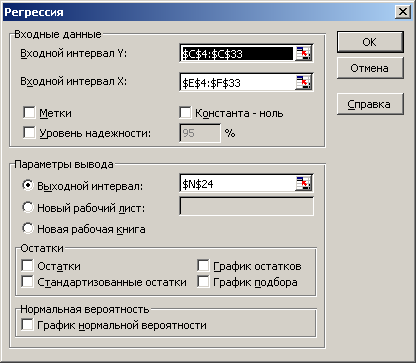 Рис. 3.2. Окно ввода параметров регрессии MS Excel Результаты работы функции приведены в таблицах 3.4, 3.5, 3.6. Результаты корреляционного анализа 
Множественный коэффициент корреляции R Коэффициент детерминации R2 Модифицированный коэффициент детерминации R Стандартная ошибка определения R Число наблюдений Таблица 3.5 Результаты дисперсионного анализа
Таблица 3.6 Результаты регрессионного анализа
Из таблицы 3.6 следует, что уравнение регрессии имеет вид y = –99,816 + 0,154·x1 + 4,459·x2 + 0,324·x3. 3) Определение значений коэффициента множественной корреляции R и коэффициента детерминации R2. Как следует из таблицы 3.2 R = 0,748; R2 = 0,560. 4) Проверка значимости уравнения регрессии (п. 2.4). Применим F-критерий Фишера. Вычислим фактическое значение критерия (2.14) 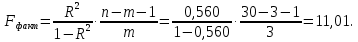 Это же значение 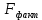 можно было взять из таблицы 3.4. можно было взять из таблицы 3.4.Определим критическое значение критерия 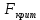 F-критерия Фишера, используя функцию MS Excel «FРАСПОБР()»: F-критерия Фишера, используя функцию MS Excel «FРАСПОБР()»:– уровень значимости α = 0,05; – число степеней свободы k1 = m = 3; k2 = n - m - 1 = 30 - 3 - 1 = 26; – 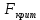 = FРАСПОБР(0,05; 3; 26) = 2,98. = FРАСПОБР(0,05; 3; 26) = 2,98.Так как 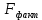 = 11,01 > = 11,01 > 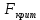 = 2,28, то делаем вывод о значимости построенного уравнения регрессии. = 2,28, то делаем вывод о значимости построенного уравнения регрессии.Из таблицы 3.5 следует, что уровень значимости уравнения регрессии α = 7,55·10-5, т. е. заведомо ниже требуемого уровня α = 0,05, т. е. уравнение значимо и при более низком уровне значимости. 5) Проверка значимости коэффициентов уравнения регрессии (п. 2.5). Применим t-критерий Стьюдента. Из таблицы 3.6 следует, что уровни значимости коэффициентов уравнения регрессии имеют значения: αa = 0,050; 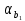 = 0,058; = 0,058; 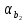 = 0,005; = 0,005; 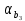 = 0,023. = 0,023.Таким образом, оценки параметров a, b2, b3 значимы при уровне значимости α = 0,05, а значение b1 не значимо при уровне значимости α = 0,05. 6) Построение уравнения линейной множественной регрессии с учетом только значимых факторов. Значимыми факторами являются x2, x3. Для построения уравнения линейной регрессии используем функцию «Сервис.Анализ данных.Регрессия» табличного процессора MS Excel (рис 3.1). Задав соответствующие диапазоны данных в окне ввода параметров регрессии (рис. 3.2), получим Множественный коэффициент корреляции R = 0,702, Коэффициент детерминации R2 = 0,493, 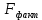 = 13,12, = 13,12,уровень значимости уравнения регрессии α = 0,0001. Таблица 3.7 |
