лабараторна 9. Практикум (раздел 3) Введение
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
|
Результаты регрессионного анализа
Из таблицы 3.7 следует, что уравнение регрессии имеет вид y = -89,520 + 4,082·x2 + 0,361·x3. 7) Проверка гипотезы о гомоскедастичности ряда остатков с уровнем значимости α = 0,05 (п. 2.9). Рассчитаем модельные значения переменной по уравнению регрессии и соответствующие остатки (табл. 3.8). Таблица 3.8 Промежуточные результаты расчета
Отсортируем данные таблицы 3.8 по переменным x2 и x3 (табл. 3.9). Таблица 3.9 Результаты сортировки данных таблицы 3.8 по переменным x2 и x3
Темным цветом в таблице 3.9 выделены данные, которые исключаются из дальнейшего рассмотрения. а) Для проверки гомоскедастичности ряда остатков по переменной x2 построим два уравнения регрессии 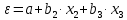 по первой и второй группе отсортированных данных по переменной x2 из таблицы 3.9 и определим остаточные суммы квадратов (S1) и (S2) остатков при n0 = 11 и р = 2: по первой и второй группе отсортированных данных по переменной x2 из таблицы 3.9 и определим остаточные суммы квадратов (S1) и (S2) остатков при n0 = 11 и р = 2:1) 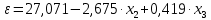 , S1 = 326,42, , S1 = 326,42,2) 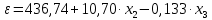 , S2 = 184,00. , S2 = 184,00.Вычислим отношение R= max(S2, S1) / min(S2, S1) = 326,42/184,00 = 1,77 и определим критическое значение F-критерия Фишера 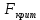 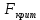 = FРАСПОБР(0,05; n0 – р; n0 – р) = =FРАСПОБР(0,05; 11–2; 11– 2) = FРАСПОБР(0,05; 9; 9) = 3,18. = FРАСПОБР(0,05; n0 – р; n0 – р) = =FРАСПОБР(0,05; 11–2; 11– 2) = FРАСПОБР(0,05; 9; 9) = 3,18.Так как не выполняется условие R = 1,77 > 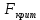 = 3,18, = 3,18,то нет оснований отвергать предположение о постоянстве дисперсии остатков (остатки гомоскедастичны) по переменной x2. 8) Для проверки гомоскедастичности ряда остатков по переменной x3 построим два уравнения регрессии 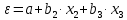 по первой и второй группе отсортированных данных по переменной x3 из таблицы 3.9 и определим остаточные суммы квадратов (S1) и (S2) остатков по первой и второй группе отсортированных данных по переменной x3 из таблицы 3.9 и определим остаточные суммы квадратов (S1) и (S2) остатков1) 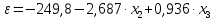 , S1 = 142,2, , S1 = 142,2,2) 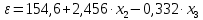 , S2 = 166,4. , S2 = 166,4.Вычислим отношение R = max(S2, S1) / min(S2, S1) = 166,4/142,2 = 1,17. Критическое значение F-критерия Фишера 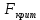 то же самое то же самое 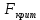 =3,18. =3,18.Так как не выполняется условие R = 1,77 > 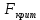 = 3,18, = 3,18,то нет оснований отвергать предположение о постоянстве дисперсии остатков (остатки гомоскедастичны) по переменной x3. 9) Построение частных уравнений регрессии (п. 3.5, формулы (3.6), (3.7)) на основании уравнения y = -89,520 + 4,082·x2 + 0,361·x3. Определим средние значения переменных используя функции СРЗНАЧ() табличного процессора MS Excel 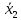 , , 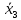 , , 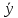 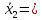 СРЗНАЧ()=37,70; СРЗНАЧ()=37,70; 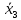 =168,27; =168,27; 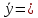 125,17. 125,17.Вычислим свободные члены частных уравнений регрессии (3.7) A2 = a + b3  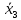 = –89,520 + 0,361·168,27 = –28,77; = –89,520 + 0,361·168,27 = –28,77;A3 = a + b2  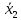 = = –89,520 + 4,082·37,70 = 64,37. = = –89,520 + 4,082·37,70 = 64,37.Частные уравнения регрессии  –28,77 + 4,082·x2, –28,77 + 4,082·x2, = 64,37 + 0,361·x3. = 64,37 + 0,361·x3.10) Определение средних частных коэффициентов эластичности (п. 3.6, формула (3.9)) 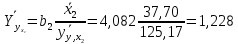 ; ;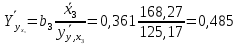 . . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||