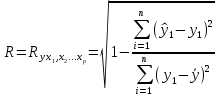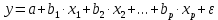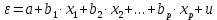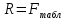лабараторна 9. Практикум (раздел 3) Введение
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
3.6. Множественная корреляция Коэффициент множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или, иначе говоря, оценивает тесноту совместного влияния факторов на результат и вычисляется по формуле (1.5).
где n – количество наблюдений; 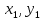 - данные наблюдений; - данные наблюдений; 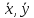 – средние значения переменных x и y; – средние значения переменных x и y; 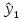 – расчетные значения переменной y, вычисленные по уравнению множественной регрессии, т. е. – расчетные значения переменной y, вычисленные по уравнению множественной регрессии, т. е. 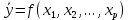 . .Коэффициент множественной корреляции изменяется от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина коэффициента множественной корреляции больше или равна максимальному парному коэффициенту корреляции 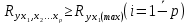 При правильном включении факторов в регрессионный анализ величина индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости. Квадрат коэффициента множественной корреляции называется коэффициентом детерминации и обозначается 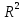 . Величина коэффициента детерминации используется для оценки качества регрессионной модели. Чем его величина больше, тем лучше данная модель согласуется с данными наблюдениями. . Величина коэффициента детерминации используется для оценки качества регрессионной модели. Чем его величина больше, тем лучше данная модель согласуется с данными наблюдениями.Низкое значение коэффициента (индекса) множественной корреляции означает, что либо в регрессионную модель не включены существенные факторы, либо рассматриваемая форма связи не отражает реальные соотношения между переменными, включенными в модель. В этом случае требуются дальнейшие исследования по улучшению качества модели и увеличению ее практической значимости. 3.7. Оценка качества результатов моделированияСтатистическая значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера (п. 2.4). Статистическая значимость коэффициентов уравнения множественной регрессии в целом оценивается с помощью t-критерия Стьюдента (п. 2.5). 3.8. Проверка остатков регрессии на гомоскедастичностьДля того чтобы МНК давал надежные оценки параметров линейной регрессии, требуется чтобы дисперсии остатков модели 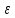
для каждого наблюдения были одинаковы. Остатки, обладающие таким свойством, называются гомоскедастичными, а не обладающие – гетероскедастичными. При нарушении гомоскедастичности мы имеем неравенства 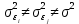 , , 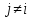 . .Для оценки гетероскедастичности можно использовать Гольдфельда-Квандта, который проверяет наличие зависимости остатков 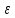 от одной из факторных переменных от одной из факторных переменных 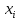 . Алгоритм применения теста Гольдфельда-Квандта состоит из следующих шагов: . Алгоритм применения теста Гольдфельда-Квандта состоит из следующих шагов:1) исходные данные наблюдений упорядочиваются по мере возрастания выбранной переменной 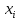 ; ;2) выделяются первые 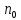 и последние и последние 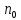 наблюдений и исключаются из рассмотрения наблюдений и исключаются из рассмотрения 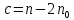 центральных наблюдений. При этом должно выполняться условие центральных наблюдений. При этом должно выполняться условие 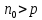 , где , где 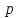 - число оцениваемых параметров; - число оцениваемых параметров;3) для каждой из групп наблюдений оцениваются уравнения регрессии остатков 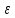 по значимым факторам по значимым факторам
4) для каждого уравнения определяются остаточные суммы квадратов ( 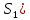 и ( и (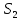 ) остатков ) остатков 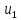 и находится их отношение: и находится их отношение: 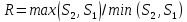 . .Если выполняется условие
где 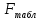 представляет собой табличное значение F-критерия Фишера при уровне значимости α и числе степенях свободы представляет собой табличное значение F-критерия Фишера при уровне значимости α и числе степенях свободы 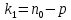 , , 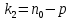 , то предпосылка о равенстве дисперсий остаточных величин отвергается с уровнем значимости α. , то предпосылка о равенстве дисперсий остаточных величин отвергается с уровнем значимости α.Чем больше величина 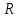 превышает табличное значение критерия превышает табличное значение критерия 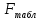 , тем более нарушена предпосылка о равенстве дисперсий остаточных величин. , тем более нарушена предпосылка о равенстве дисперсий остаточных величин.Авторами метода рекомендовано для случая одного фактора 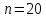 приниматься приниматься 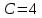 , при , при 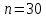 принимать принимать 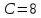 , при , при 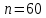 принимать принимать 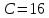 . . |