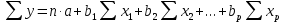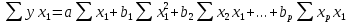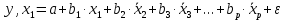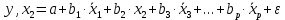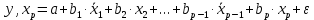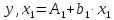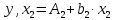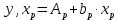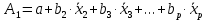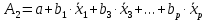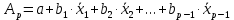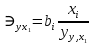лабараторна 9. Практикум (раздел 3) Введение
 Скачать 0.79 Mb. Скачать 0.79 Mb.
|
3.4. Оценка параметров уравнения множественной регрессииДля оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений регрессии строится система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии. В случае линейной множественной регрессии (3.2) система нормальных уравнений имеет следующий вид:
………………………………………………………………………………………. 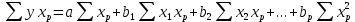 3.5.Частные уравнения регрессииУравнения линейной множественной регрессии (3.2) позволяет построить, так называемые, частные уравнения регрессии, показывающие зависимость результативного признака от отдельного фактора, при исключении влияния остальных факторов, входящих в уравнение множественной регрессии. Частные уравнения регрессии получаются из уравнения множественной регрессии (3.2) с помощью замены всех факторов, кроме одного из их средние значения:
Уравнения (3.5) можно представить в виде
где
В отличие от парной регрессии, частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Частные уравнения регрессии позволяют определить частные коэффициенты эластичности
где 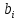 – коэффициенты регрессии для фактора – коэффициенты регрессии для фактора 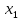 в уравнении множественной регрессии; в уравнении множественной регрессии; 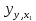 - значение результативного фактора, полученное из частного уравнения регрессии при данном значении фактора - значение результативного фактора, полученное из частного уравнения регрессии при данном значении фактора 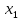 . .Средние показатели эластичности можно сравнить друг с другом и соответственно ранжировать факторы по силе их воздействия на результат. Средние коэффициенты эластичности для линейной множественной регрессии рассчитываются по формуле
и показывают, на сколько процентов в среднем по совокупности изменится результат y от своей величины при изменении фактора x на 1% от своего значения при неизменных значения других факторов. |