лабораторный практикум. Практикум волгоград 2014 Печатается по решению редакционноиздательского совета

• Название: Практикум волгоград 2014 Печатается по решению редакционноиздательского совета
• Анкор: лабораторный практикум
• Дата: 26.04.2023
• Размер: 5.21 Mb.
• Имя файла: LABORATORNAYa.doc
• Тип: Практикум; #1091404
• страница: 1 из 9

ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра лазерной физики


В.Н. Храмов, С.А. Куценко, Теряева С.В.


ОПТИКА

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

Волгоград 2014
Печатается по решению

редакционно-издательского совета

Волгоградского государственного университета
Рецензенты:

д-р техн. наук, проф. ВолГУ В.А. Михайлова;

д-р физ.-мат. наук, проф. ВолгГТУ А. Г. Шеин;
Храмов В.Н., Куценко С.А., Теряева С.В.,

Оптика. Лабораторный практикум: Учебно-методическое пособие для вузов / ВолГУ. – Волгоград: Изд-во ВолГУ, 2014. – 170с.: ил.

В данный сборник включены описания тринадцати лабораторных работ, являющихся неотъемлемой частью курсов «Общий физический лабораторный практикум», «Физика», «Основы оптики», рекомендованных Федеральными Государственными образовательными стандартами высшего профессионального образования направлений 200400 – Оптотехника., 200500 «Лазерная техника и лазерные технологии», 011200 «Физика», 11800 «Радиофизика», 200400 «Радиотехника», 200700 «Инфокоммуникационные технологии и системы связи» 090900 «Информационная безопасность», 090903 «Информационная безопасность автоматизированных систем». Лабораторный практикум охватывает следующие основные разделы оптики: «Геометрическая оптика», «Отражение и преломление света на границе двух сред», «Поляризация света», «Интерференция света», «Дифракция света», «Взаимодействие света с веществом», «Оптические спектральные приборы».

В каждом методическом указании достаточно подробно изложена теория исследуемых физических эффектов, описаны лабораторные установки и порядок выполнения работ, приведены контрольные вопросы и задания.



ГЕОМЕТРИЧЕСКАЯ ОПТИКА

Лабораторная работа

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ КАРДИНАЛЬНЫХ ЭЛЕМЕНТОВ

ОПТИЧЕСКОЙ СИСТЕМЫ

ЦЕЛЬ РАБОТЫ: изучение основных положений геометрической оптики, определение фокусных расстояний тонких линз, определение положения кардинальных элементов сложной оптической системы.

ПРИНАДЛЕЖНОСТИ: осветитель, матовое стекло с перекрестием, собирающая и рассеивающая линзы, сложная оптическая система (объектив), зрительная труба, линейка, экран, оптическая скамья с набором рейтеров.

1. 
   Теоретическая часть
   

Геометрической (лучевой) оптикой называется раздел оптики, в котором изучаются законы распространения света на основе представлений о световых лучах. Под световым лучом понимают линию, вдоль которой распространяется поток световой энергии. Понятием луча можно пользоваться только в случае, когда можно пренебречь дифракционными явлениями на каких-либо неоднородностях. Это допустимо, если длина волны много меньше характерных размеров этих неоднородностей. Таким образом, геометрическую оптику можно рассматривать как отдельную область физической оптики, при стремлении длины волны излучения к нулю. Законы геометрической оптики позволяют создать упрощенную, но в большинстве случаев достаточно точную теорию оптических систем.

Оптической системой (ОС) называют совокупность оптических деталей (линз, призм, зеркал и т.п.), предназначенную для формирования пучков световых лучей. Геометрическая оптика в основном объясняет образование оптических изображений, дает возможность вычислять аберрации оптических систем и разрабатывать методы их исправления, выводить энергетические соотношения в световых пучках, проходящих через оптические системы.

1.1. Прохождение лучей в центрированных оптических системах

Линзами называют детали из оптически прозрачных однородных материалов, ограниченные двумя преломляющими поверхностями, из которых хотя бы одна является поверхностью тела вращения (сфера, асферическая или цилиндрическая поверхность).

Рассмотрим прохождение лучей через сферическую линзу, не накладывая ограничений на ее толщину (рис.1). Обозначения видны из рисунка.


Рис. 1



Оптической осью линзы называется прямая, проходящая через центры кривизны ее поверхностей (в данном построении это ось Z). Если оптическая ось совпадает с осью симметрии ОС, то такая система называется центрированной. Свет распространяется вдоль положительного направления оси Z. Луч света лежит в плоскости XZ. Плоскость, образованная оптической осью и лучом, пересекающим эту ось, называется меридиональной плоскостью. r₁ и r₂ – радиусы кривизны 1-й и 2-й сферических поверхностей линзы (r₂ на рис.1 не показан, чтобы не загромождать рисунок). Весь расчет проводится в параксиальном приближении: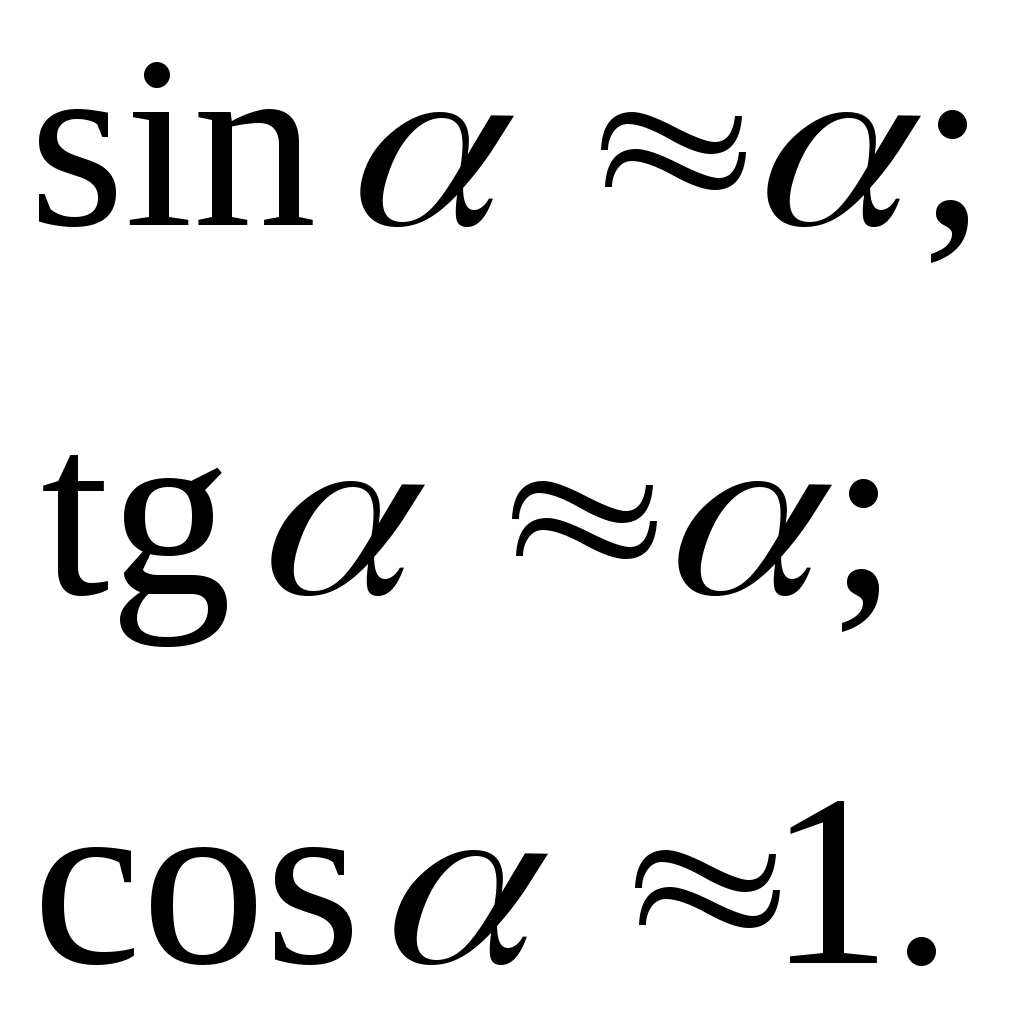

(1)

Рассмотрим преломление на первой сферической поверхности. В точке P₁ закон Снеллиуса в параксиальном приближении имеет вид:

(2)

Используя геометрические соотношения между углами:

(3)

и учитывая, что в параксиальном приближении 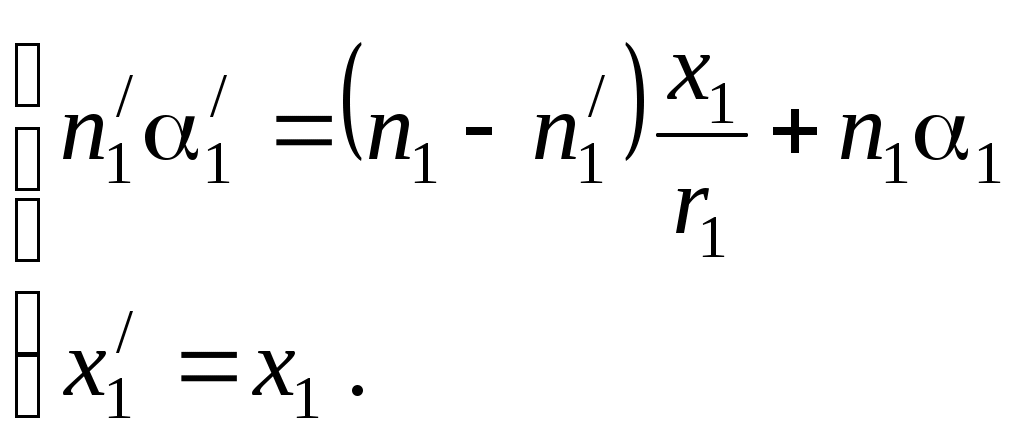из (2) и системы используемых обозначений получаем:

(4)

Система уравнений (4) позволяет, задав координаты падающего на первую поверхность линзы луча (n₁₁; x₁), найти координаты (n₁^/₁^/; x₁^/) преломленного в линзе луча. Полученную систему удобно записать в матричном виде: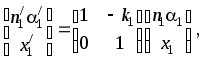

(5)

где k₁=(n₁^/–n₁)/r₁ называется преломляющей силой первой поверхности, а матрица (6)

называется преломляющей матрицей первой поверхности.

Рассмотрим распространение луча внутри линзы в параксиальном приближении. Преломленный луч, после прохождения внутри линзы, падает на её вторую поверхность на расстоянии x₂ от оси:

(7)

Отметим, что величина  в параксиальном приближении практически равна толщине линзы А₁А₂ вдоль оси. С учетом, что 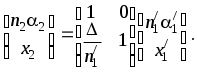получаем в 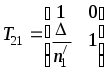матричном виде: (8)

Матрица (9)

описывает распространение луча от первой поверхности линзы ко второй и называется передаточной матрицей.

Преломление луча на второй сферической поверхности рассматривается точно так же, как и на первой поверхности. Величина k₂=(n₂^/ –n₂)/r₂ называется преломляющей силой второй поверхности, а матрица R₂– преломляющей матрицей второй поверхности:

(10)

Знаки всех величин в приведенных выражениях необходимо брать с учётом правил знаков: если встречаемая лучом преломляющая поверхность выпуклая, то её радиус кривизны надо брать с положительным знаком, а если вогнутая – с отрицательным; углы , отсчитываемые от оси Z против часовой стрелки, положительны, а по часовой стрелке – отрицательны; расстояния, отсчитываемые по Z (по рис.1 – слева направо), положительны, а против Z (справа налево) – отрицательны; расстояния от оси Z, отсчитываемые вверх, положительны, вниз – отрицательны.

Объединим полученные результаты и рассмотрим распространение луча через линзу в целом. Используя (5) – (10), получаем связь между характеристиками луча на выходе из линзы и входе в неё: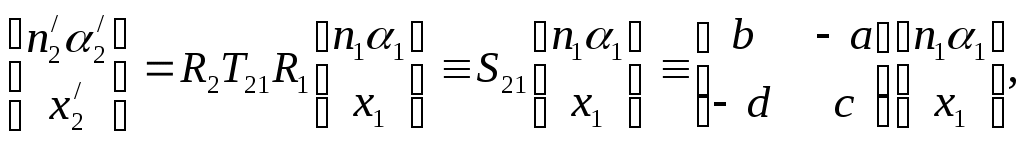

(11)

где a, b, c, d называются постоянными Гаусса. Они равны: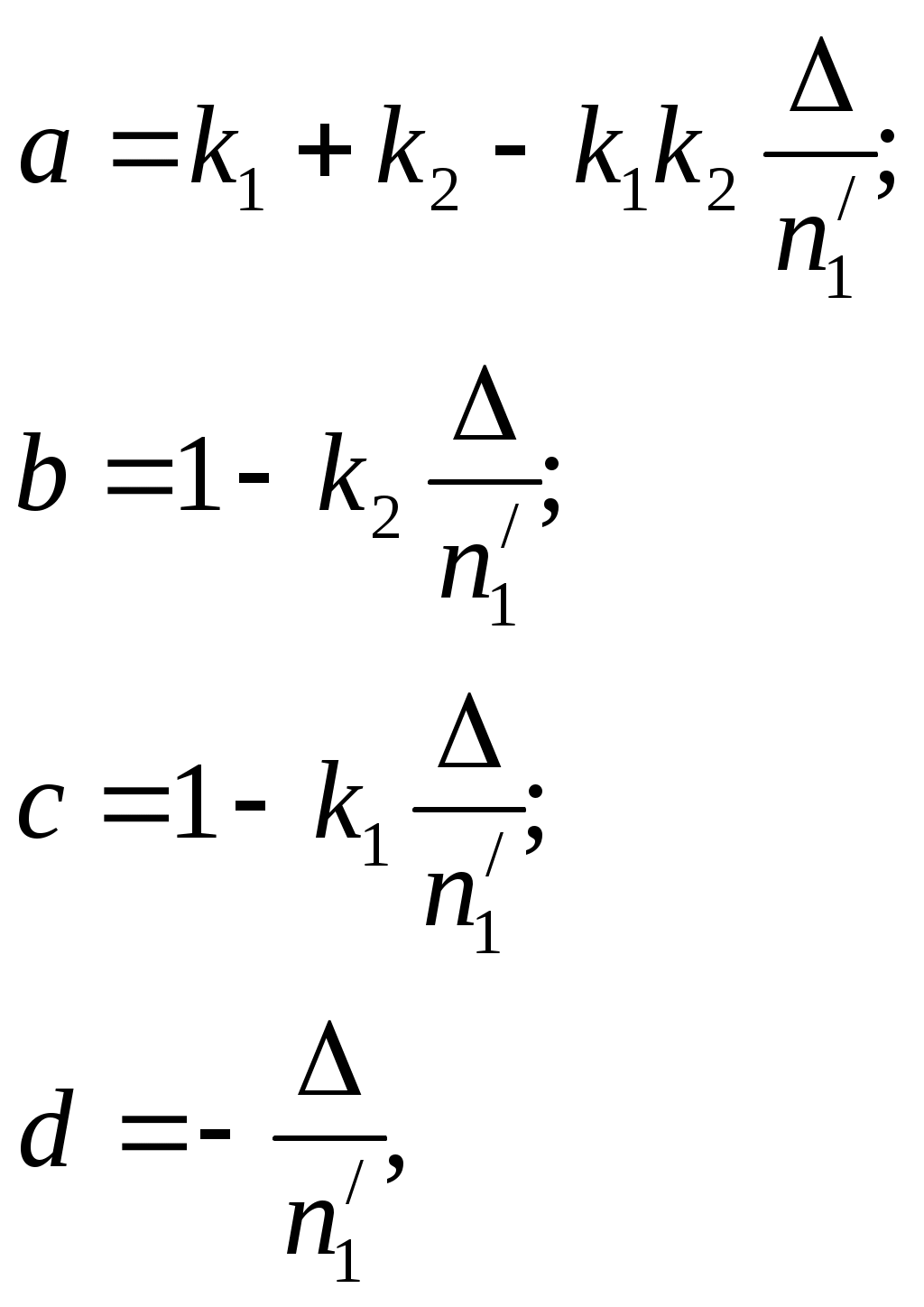

(12)

Независимыми являются только три из четырех постоянных Гаусса, т.к. . Матрица S₂₁ полностью описывает рассмотренную оптическую систему.

1.2. Преобразование луча от плоскости предмета к плоскости изображения

Пусть из точки некоторой плоскости (плоскости предмета), расположенной на расстоянии l слева от точки А₁ и выше оптической оси на расстоянии x, выходит луч с координатами (n₁₁, x) и падает на рассматриваемую линзу. В некоторой плоскости, расположенной справа от точки А₂ на расстоянии l^/ луч характеризуется координатами (n₂^/₂^/, x^/). Между этими парами координат по приведенным выше правилам получаем соотношение:

(13)

(Знак l уже учтён)

Перемножив матрицы в (13), получим:

(14)

Матрица Q₂₁ называется матрицей преобразования от предмета к изображению: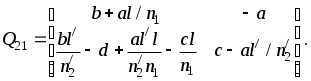

(15)

Обозначим – линейное (поперечное) увеличение оптической системы. Введем понятие изображения.

Под изображением понимается такое отображение плоскости предмета на плоскость, называемую плоскостью изображения, когда все лучи, исходящие от точки предмета, сходятся после преломления в оптической системе в одной точке плоскости изображения и все точки отображаются с одинаковым увеличением.

Исходя из этого определения, в точке изображения увеличение М не должно зависеть от угла ₁. Поэтому соответствующий член в матрице Q₂₁ обращается в нуль:

(16)

Из определения увеличения имеем:

(17)

Тогда матрица преобразования от предмета к изображению принимает вид: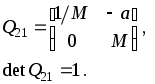

(18)

1.3. Кардинальные элементы оптической системы

Плоскости H и H^/, увеличение для точек которых М = 1, называются главными плоскостями, а их пересечения с осью системы (осью Z) – главными точками системы. Найдём из (17) их положение:

(19)

где l_H – отсчёт положения плоскости H относительно точки А₁; l_H^/ – отсчёт положения плоскости H^/ относительно точки А₂ .

Точка на оси системы, в которой сходятся лучи, падающие на оптическую систему параллельно главной оптической оси (т.е. точка с M = 0) и точка, выйдя из которой лучи после прохождения оптической системы становятся параллельными оптической оси (т.е. с M = ), называются фокусами оптической системы. Плоскости, проходящие через фокусы перпендикулярно оптической оси, называются фокальными. Найдём из (17) их положение: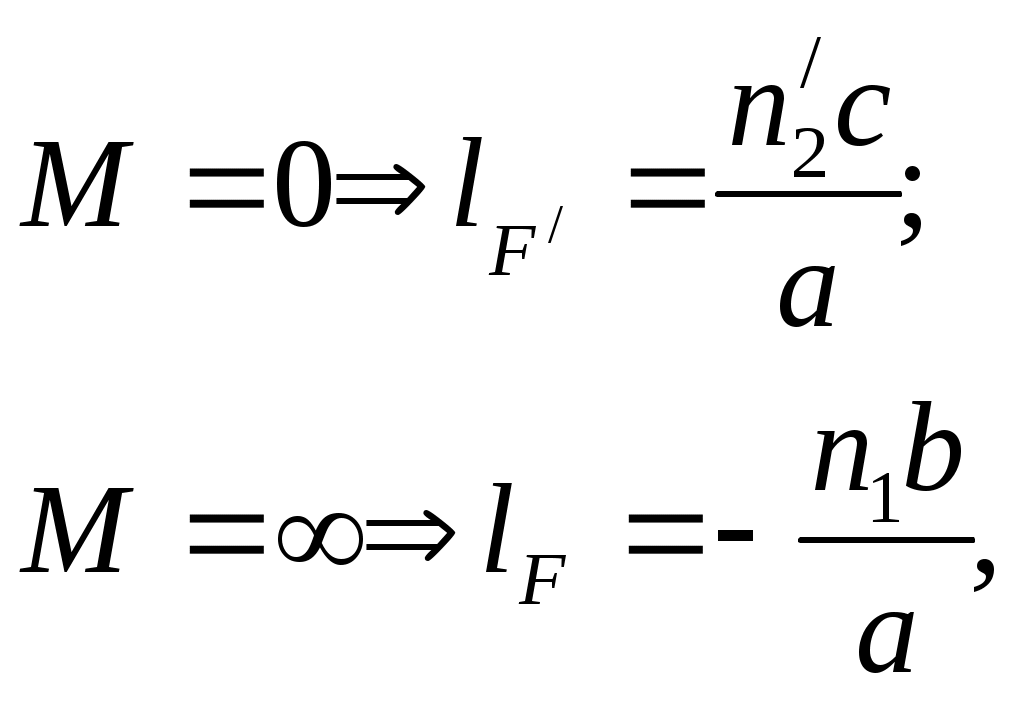

(20)

где l_F– отсчёт положения переднего фокуса относительно точки А₁ , l_F^/ – отсчёт положения заднего фокуса относительно точки А₂ .

Расстояние f между передней главной точкой и передним фокусом называется передним фокусным расстоянием; расстояние f^/между задней главной точкой и задним фокусом ‑ задним фокусным расстоянием:

(21)

Главные и фокальные плоскости называются кардинальными элементами оптической системы. Их положение позволяет полностью описать преломление лучей в оптической системе и построить изображение заданного предмета (рис.2).


Рис. 2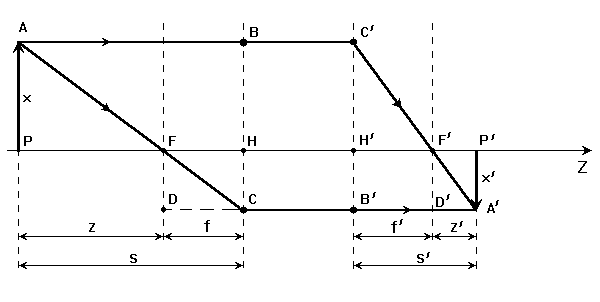


1.4. Уравнение линзы

Из подобия треугольников CDF, ABC, FPA (рис.5.4) следует:

(22)

а из подобия треугольников A^/D^/F^/, F^/H^/C^/, A^/B^/C^/ следует:

(23)

Из этих соотношений имеем: (24)

а отсюда получаем уравнение линзы в форме Ньютона:

(25)

Из этих же уравнений можно получить уравнение линзы в форме Гаусса:

(26)

Увеличение линзы определяется из формулы:

(27)

1.5. Тонкие линзы

Пусть 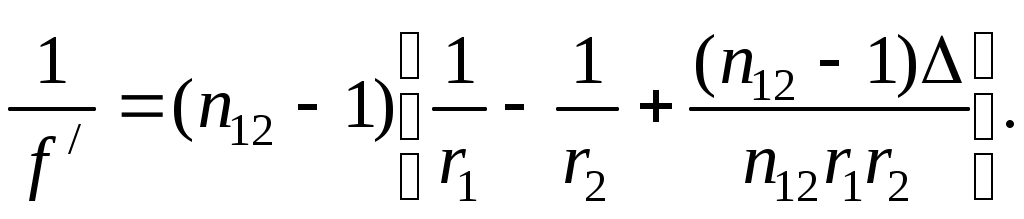– относительный коэффициент преломления и . Тогда из (12) и (21) следует выражение для фокусного расстояния линзы через относительный коэффициент преломления и её геометрические параметры:

(28)

Тонкой линзой называется линза, для которой можно пренебречь третьим слагаемым в скобках (28), что соответствует малости толщины линзы по сравнению с каждым радиусом кривизны:

(29)

С поверхностями тонкой линзы совпадают обе главные плоскости. Фокусное расстояние становится равным отсчёту от линзы до фокуса. При этом условии матрица с коэффициентами Гаусса для тонкой линзы принимает вид:

(30)

Величина (31)

называется оптической силой линзы. Оптическая сила измеряется в диоптриях (1 дптр соответствует фокусному расстоянию в воздухе 1 м). Оптическая сила положительна для собирающих линз и отрицательна для рассеивающих.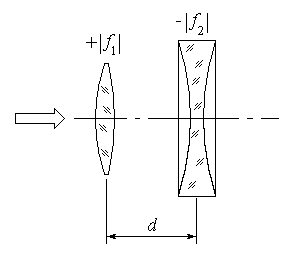

Рассмотрим в качестве примера простейшую систему из двух тонких линз (рис. 3).

Тогда матрица S, описывающая данную систему, будет получаться путём перемножения матриц: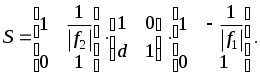

(32) Рис. 3

Далее находятся постоянные Гаусса, а из них кардинальные элементы данной оптической системы. Отсчет для передних главной точки и фокуса идет от первой линзы, а для задних кардинальных точек – от последней линзы по приведенному выше правилу знаков.

Примечание

При общем теоретическом введении выполнение данной лабораторной работы рекомендуется методически разбить на две последовательные части:

1. Определение фокусного расстояния тонкой линзы.

2. Определение фокусного расстояния и положения кардинальных элементов сложной оптической системы.

2. Описание лабораторных установок

2.1. Установка для измерений фокусных расстояний тонких линз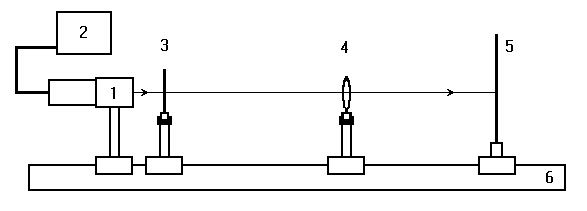


Лабораторная установка (рис.4) состоит из осветителя, включающего в себя излучатель (1) и блок питания (2) матового стекла (3) с перекрестием, играющим роль предмета, собирающей линзы (4), фокусное расстояние которой требуется определить, и экрана (5), на котором наблюдается действительное изображение предмета (3). Все элементы установлены на оптической скамье (6).

Рис. 4. Схема лабораторной установки

Линзы закреплены в оправах и устанавливаются в рейтеры, которые могут перемещаться вдоль оптической скамьи. Положение всех элементов на скамье определяется с помощью шкалы, прикрепленной к оптической скамье, или линейки. Все оптические детали центрируются, т.е. должны быть установлены так, чтобы их центры лежали на одной высоте, оптические оси линз были параллельны ребру оптической скамьи, плоскость экрана перпендикулярна оптической оси линз.

2.2. Установка для измерения положения кардинальных элементов сложной оптической системы

Лабораторная установка (рис.5) состоит из осветителя, включающего в себя излучатель (1) и блок питания (2), матового стекла (3) с перекрестием, играющим роль предмета, объектива (сложной оптической системы) (4), фокусное расстояние и положение кардинальных элементов которого требуется определить, зрительной трубы (5), настроенной на бесконечность. Все элементы установлены на оптической скамье (6). Наблюдение п 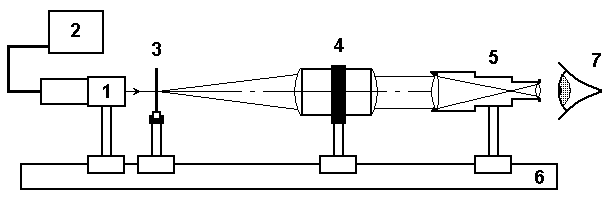роводится глазом (7).

Рис. 5. Схема лабораторной установки
3. Порядок выполнения работы «Определение фокусного расстояния тонкой линзы»

3.1. Определение фокусного расстояния собирающей линзы по расстояниям от предмета до линзы и от линзы до изображения.

3.1.1. Поместив экран достаточно далеко от предмета, поместить между ними собирающую линзу и передвигать ее до тех пор, пока на экране не получится отчетливое изображение предмета (уменьшенное или увеличенное). Отсчитать по шкале линейки положения предмета, линзы и экрана.

3.1.2. Передвинуть экран и предмет в другое положение и вновь зафиксировать по шкале положения экрана, линзы и предмета.

3.1.3. Из-за неточности визуальной оценки резкости изображения измерения следует проделать не менее десяти раз. Часть измерений полезно произвести при увеличенном, а часть – при уменьшенном изображении предмета.

3.1.4. По данным каждого измерения вычислить фокусное расстояние линзы по формуле: , (33)

где а – расстояние от предмета до линзы; b – расстояние от изображения до линзы.

3.1.5. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.2. Определение фокусного расстояния собирающей линзы по размерам предмета и его изображения и по расстоянию от изображения до линзы

3.2.1. Поместить собирающую линзу между предметом и экраном в таком положении, чтобы на экране появилось сильно увеличенное отчетливое изображение предмета.

3.2.2. Измерить при помощи линейки длину какого-либо штриха изображения (горизонтального или вертикального). Измерив расстояние от изображения (экрана) до линзы, найти фокусное расстояние линзы по формуле: , (34)

где b – расстояние от изображения до линзы, l – величина предмета (длина штриха предмета), L – величина изображения (длина штриха изображения).

3.2.3. Измерить расстояние от линзы до экрана не менее трёх раз. Для каждого из значений найти f. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.3. Определение фокусного расстояния собирающей линзы по величине перемещения линзы (способ Бесселя)

3.3.1. Установив предмет и экран на расстоянии А > 4f(ориентировочно значение f взять из предыдущих опытов), поместить линзу между ними и, передвигая ее, получить на экране отчетливое изображение предмета, например, увеличенное. Отсчитать по шкале положение линзы.

3.3.2. Проделать п. 3.3.1 не менее трёх раз. За положение линзы вновь принять среднее арифметическое отдельных отсчетов.

3.3.3. Передвигая линзу, получить второе отчетливое изображение предмета – уменьшенное. Снять отсчет положения линзы.

3.3.4. Проделать п. 3.3.3. не менее трёх раз. За положение линзы вновь принять среднее арифметическое отсчетов.

3.3.5. Измерить расстояние А между предметом и экраном.

3.3.6. Вычислить величину перемещения линзы l как разность отсчетов положения линзы.

3.3.7. Вычислить фокусное расстояние линзы по формуле:

. (35)

Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.4. Определение фокусного расстояния рассеивающей линзы

Отрицательная линза имеет мнимые фокусы. Фокусное расстояние рассеивающей линзы можно определить, если использовать действительное изображение предмета, полученное с помощью вспомогательной положительной линзы, играющее роль предмета для отрицательной линзы. Для этого необходимо использовать положительную линзу с оптической силой большей, чем модуль оптической силы исследуемой отрицательной линзы. В этом случае можно получит положительную оптическую систему, состоящую из собирающей и рассеивающей линзы.

3.4.1. Поместить между предметом и экраном собирающую линзу и получить на экране отчетливое уменьшенное изображение. Полученное с помощью собирающей линзы изображение А_рбудет играть роль предмета для рассеивающей линзы (рис. 6).

3.4.2. Не убирая экрана, между ним и собирающей линзой поместить рассеивающую линзу. Замерить расстояние b между рассеивающей линзой и экраном.

Р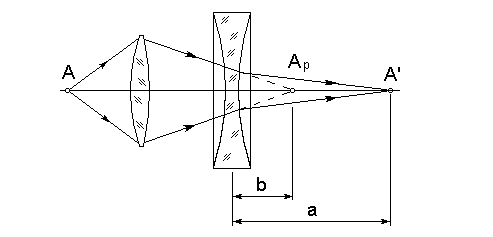
ис. 6

3.4.3. Отодвигая экран, снова добиться четкого изображения А^/предмета A.

3.4.5. Замерить расстояние от рассеивающей линзы до экрана a.

3.4.6. Рассчитать модуль фокусного расстояния рассеивающей линзы по следующей формуле: . (36)

3.4.7. Измерения повторить не менее пяти раз. Провести статистическую обработку результатов с доверительной вероятностью 90%.
4. Порядок выполнения работы «Определение фокусного расстояния и положения кардинальных элементов сложной оптической системы»

В данной работе сначала определяется фокусное расстояние сложного объектива по способу Аббе. Затем с помощью зрительной трубы, настроенной на бесконечность, определяют положения фокусов. Отложив от фокусов отрезки, равные фокусному расстоянию, находят положение главных плоскостей.

4.1. Поместить сложный объектив между предметом и экраном.

4.2. Передвинув экран на край оптической скамьи и перемещая объектив, получить на экране сначала увеличенное изображение предмета, затем уменьшенное изображение. Определить в обоих случаях линейные увеличения изображений М₁ и М₂.

4.3. Измерить величину перемещения объектива из первого положения во второе.

4.4. Рассчитать фокусное расстояние объектива по формуле:

. (37)

4.5. Убрать экран, а на его место поместить зрительную трубу, настроенную на бесконечность.

4.6. Перемещать объектив вдоль оптической скамью до тех пор, пока в поле зрения трубы не появится отчетливое изображения предмета. Измерить расстояние от передней преломляющей поверхности объектива по переднего главного фокуса.

4.7. Перевернуть объектив на 180. Повторив п.4.6., получить расстояние от задней преломляющей поверхности до заднего фокуса.

4.8. Отложив отрезки (см. формулы (19) – (21)), найти положения фокусов и главных точек объектива относительно преломляющих поверхностей.

4.9. Повторить п.4.1 – 4.8 не менее пяти раз. Провести статистическую обработку результатов с доверительной вероятностью 90%.

4.10. По предоставленным преподавателем данным о параметрах линз и их расположении в оптической системе объектива рассчитать положения его кардинальных элементов. Изобразить полученные результаты на рисунке. Сравнить экспериментальные и расчетные результаты.
5. Контрольные вопросы и задания

1. Дайте определения кардинальных элементов оптической системы. Объясните физический смысл главных и фокальных плоскостей и точек.

2. Выведите формулы (33) – (37).

3. Может ли двояковогнутая линза быть собирающей? Может ли двояковыпуклая линза быть рассеивающей?

4. Две собирающие линзы с фокусными расстояниями f₁ и f₂ установлены на расстоянии L друг от друга, так что их оптические оси совпадают. Найти фокусное расстояние этой системы линз.

5. Фокусное расстояние тонкой стеклянной линзы в воде равно f. При погружении ее в сероуглерод (n=1,63) фокусное расстояние изменилось на f. Чему равны фокусное расстояние линзы и показатель преломления стекла?

6. Расстояние между двумя точечными источниками равно L. Где нужно поместить собирающую линзу с фокусным расстоянием f, чтобы изображения обоих источников совпали?

7. С помощью тонкой собирающей стеклянной линзы с показателем преломления n=1,5 получено действительное изображение предмета на расстоянии 10 см от линзы. После того как предмет и линзу поместили в воду, не меняя расстояния между ними, изображение получилось на расстоянии 60 см от линзы. Найти фокусное расстояние линзы в воздухе, если показатель преломления воды n_в = 1,33.

8. Двояковыпуклая линза с радиусами кривизны поверхностей r₁= 6 см и r₂= ‑3 см, толщиной по оси =1,5 см, показателем преломления n=1,5 находится в воздухе. Найти фокусное линзы и расположение кардинальных плоскостей.

9 . Из плоскопараллельной стеклянной пластинки изготовлены три линзы (см. рис.). Фокусное расстояние линз 1 и 2, сложенных вместе, равно –f₁₂, фокусное расстояние линз 2 и 3 равно –f₂₃. Определить фокусное расстояние каждой линзы.

1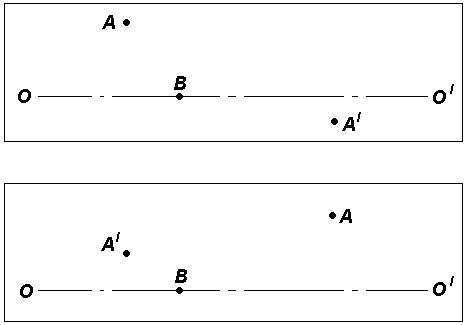
0. На рисунках указано положение оптической оси, предмета А и его изображения А^/. Определить положение линзы и ее фокусов.

Построить изображение точки В.

11. Оптическая сила тонкой линзы в воздухе и в жидкости с неизвестным показателем преломления равна соответственно Ф₀ и –Ф₁. Чему равен показатель преломления жидкости, если у стекла линзы он равен n?

1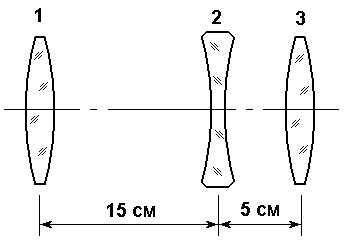
2. Найти положение кардинальных элементов системы с тонкими линзами, показанной на рисунке, если f₁= 10 см, f₂= ‑20 см. f₃= 9 см.