лабораторный практикум. Практикум волгоград 2014 Печатается по решению редакционноиздательского совета

• Название: Практикум волгоград 2014 Печатается по решению редакционноиздательского совета
• Анкор: лабораторный практикум
• Дата: 26.04.2023
• Размер: 5.21 Mb.
• Имя файла: LABORATORNAYa.doc
• Тип: Практикум; #1091404
• страница: 6 из 9

ПОЛЯРИЗАЦИЯ СВЕТА

Лабораторная работа

ЛИНЕЙНЫЙ ЭЛЕКТРООПТИЧЕСКИЙ ЭФФЕКТ

(ЭФФЕКТ ПОККЕЛЬСА)
ЦЕЛЬ РАБОТЫ: изучение линейного электрооптического эффекта и закономерностей прохождения поляризованного света через анизотропную среду.
ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, электрооптический модулятор, источник питания модулятора, поляризатор, фотоприемник, оптическая скамья.
1. Теоретическая часть
Электрооптический эффект состоит в изменении показателя преломления среды под действием электрического поля. Это изменение может быть как первого (линейный электрооптический эффект Поккельса), так и второго (квадратичный электрооптический эффект Керра) порядков относительно приложенного поля.

Изменение показателя преломления среды под действием электрического поля широко используется в лазерной физике и технике. Сюда следует отнести электрооптические затворы для модуляции добротности лазеров, системы сканирования световых пучков, модуляция света в приемо-передающих устройствах систем оптической связи и т.д.
1.1. Распространение света в анизотропной среде [1¸6, 10]
В изотропной среде связь между вектором напряженности электрического поля E и вектором индукции D дается соотношением

(1)

где e – постоянная скалярная величина, не зависящая от направления распространения волны, называемая диэлектрической проницаемостью. Поэтому вектор D совпадает по направлению с вектором E.

В случае анизотропной среды каждая компонента D зависит от величины всех трех составляющих электрического поля E :

(2)

(Индексы i, j=1,2,3 соответствуют декартовым координатам x,y,z.)

Коэффициенты e_ij являются компонентами тензора второго ранга –тензора диэлектрической проницаемости. Всю совокупность возможных значений диэлектрической проницаемости можно представить при помощи трехосного эллипсоида с осями x, y, z. Значение диэлектрической проницаемости для любого направления выражается длиной радиус-вектора эллипсоида, проведенного по этому направлению. Три значения диэлектрической проницаемости e_x, e_y, e_z , соответствующие полуосям эллипсоида, называются главными значениями диэлектрической проницаемости.

Используя связь между D и E, характеризующую анизотропию среды, можно решить систему уравнений Максвелла, причем в качестве осей координат удобно выбрать главные направления диэлектрической проницаемости (главные оси кристалла) ([1] ¸ [6]). Распространяющаяся в анизотропной среде электромагнитная волна обладает следующими особенностями [2]:

1. 
   По заданному направлению r могут распространяться две плоских линейно поляризованных волны с двумя различными фазовыми скоростями, соответствующими двум различным плоскостям колебания электрического вектора волны. Эти две плоскости колебания определяются свойствами кристалла (тензором диэлектрической проницаемости) и всегда взаимно перпендикулярны.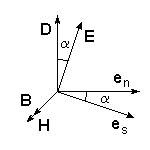
   

Рис. 1
2. В плоскости волнового фронта, т.е. в плоскости, перпендикулярной r, расположен вектор индукции D и вектор напряженности магнитного поля H, совпадающий по направлению с вектором магнитной индукции B = mH (не будем рассматривать магнитную анизотропию, т.к. она в оптическом диапазоне встречается и используется крайне редко). Вектор же напряженности электрического поля E в анизотропной среде не совпадает с D и образует некоторый угол a (рис.1).
Плоскость фронта волны, распространяющейся вдоль вектора e_n есть плоскость DH. Плоскость EH, обладающая тем свойством, что перпендикуляр к ней совпадает с направлением энергии световой волны (вектором Пойнтинга), повернута относительно DH на угол a. Таким образом, в анизотропной среде в общем случае направление энергии (луча) e_s не совпадает с направлением волновой нормали . Совпадение имеет место только в том случае, если e_n направлено вдоль одного из трех главных осей кристалла.

В оптике обычно имеют дело не с диэлектрической проницаемостью среды, а с показателем преломления n = e^1/2 , определяющем фазовую скорость распространения света v = c/n .

Для нахождения показателя преломления в анизотропной среде строят эллипсоид, называемый оптической индикатрисой. Если X,Y,Z – главные оси кристалла, то уравнение оптической индикатрисы имеет вид: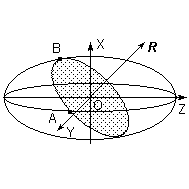

(3)

где – главные показатели преломления среды.




Рис. 2
Оптическая индикатриса имеет следующее важное свойство. Проведем из начала координат прямую OR в произвольном направлении (рис.2). Построив центральное сечение индикатрисы, перпендикулярное этой прямой, получим эллипс. Тогда показатели преломления для двух волн с волновой нормалью OR равны длинам полуосей этого эллипса OA и OB. Направление поляризаций волн совпадает с направлением осей эллипса. Вектор индукции D в плоско поляризованной волне, показатель преломления для которой равен OA, колеблется параллельно OA. Аналогично в волне для которой показатель преломления равен OB, вектор D колеблется параллельно OB. Отсюда, как частный случай, следует, что для волн с волновой нормалью X показатели преломления равны n_y и n_z, а вектор D в этих волнах параллелен соответственно Y или Z.

Симметрия кристалла налагает определенные требования на форму и ориентацию оптической индикатрисы. Например, для кубических кристаллов симметричными преобразованиями (т.е. такими преобразованиями, после которых кристалл переходит сам в себя) являются повороты относительно всех трех его осей. Отсюда следует, что оптическая индикатриса кубических кристаллов является сферой. Т.к. все центральные сечения индикатрисы в этом случае представляют окружности, эти кристаллы не обладают анизотропией.

Для гексагональных, тетрагональных (к этому классу относятся кристаллы дигидрофосфата калия KH₂PO₄ (сокращенно KDP)) и тригональных (ниобат лития LiNbO₃) кристаллов индикатриса представляет собой эллипсоид вращения вокруг главной оси симметрии. Принимая эту ось за ось z, уравнение индикатрисы можно записать в виде:

(4)

Центральное сечение, перпендикулярное главной оси (и только это сечение), есть окружность радиуса n_o. Поэтому для света с волновой нормалью, направленной вдоль главной оси Z, двулучепреломление отсутствует. В направлении, перпендикулярном плоскости кругового сечения, всем волнам соответствует одна и та же скорость, поляризация может быть любой. Направление, перпендикулярное круговому сечению, называется оптической осью кристалла. Для волн, идущих вдоль оптической оси среда ведет себя как изотропная. Такие кристаллы с одним круговым сечением индикатрисы называются одноосными.

Для трех остальных кристаллографических систем (орторомбической, моноклинной и триклинной) индикатриса является трехосным эллипсоидом. Она имеет два круговых сечения. Такие кристаллы называются двуосными.

Плоскость, проходящая через луч, направленный под углом к оптической оси и оптическую ось, называется главной. Из этого определения и определения главной оси следует, что у волны, вектор E которой направлен перпендикулярно главной плоскости, скорость не зависит от направления. Такая волна называется обыкновенной. Соответствующие ее параметры (скорость, показатель преломления) обозначаются индексом “о” (“ordinary”). У волны, вектор E которой лежит в главной плоскости, скорость зависит от направления, т.к. соответствующая полуось эллипса в сечении эллипсоида изменяется с изменением направления волны. Такая волна называется необыкновенной. Соответствующие ей параметры (скорость, показатель преломления) обозначаются индексом “е” (“extraordinary”) . Т.е., показатель преломления необыкновенной волны – величина переменная, зависящая от направления. Значение n_e, приводящееся для данного кристалла в справочной литературе – это максимально отличающееся от “обыкновенного” показателя преломления n_oзначение. Кристалл называется положительным, если n_e – n_o > 0, и отрицательным при n_e – n_o < 0 (кристаллы KDP и ниобата лития являются отрицательными).

Рассмотрим распространение поляризованного излучения в кристаллической пластинке. Линейно поляризованный свет, падая на кристалл, дает начало двум когерентным волнам, распространяющимся с различной скоростью и приобретающим после прохождения пластинки разность фаз, зависящую от толщины кристалла и различия в показателях преломления обеих волн. Так как колебания в этих волнах взаимно перпендикулярны, то они в общем случае ведут к образованию эллиптически поляризованного света. В точках, соответствующих различным разностям хода, форма и ориентация эллипсов могут быть различными, но интенсивность света везде одна и та же. Поместив после кристалла анализатор, мы от каждой волны пропускаем лишь ту компоненту колебания, которая параллельна его плоскости поляризации. Разность фаз между рассматриваемыми волнами на выходе кристаллической пластинки толщиной l определяется формулой:

(5)

где n₁ , n₂– показатели преломления для двух волн, l – длина волны света.
1.2. Эффект Поккельса
Эффект Поккельса возможен лишь в кристаллах, не имеющих центра симметрии. В кристаллах, имеющих центр симметрии, возможен только квадратичный эффект Керра.

В результате наложения электрического поля на кристалл происходят поворот и деформация оптической индикатрисы. Если в качестве координатных осей выбрать главные оси кристалла, то в отсутствие электрического поля уравнение оптической индикатрисы можно записать в виде:

(6)

где , а индекс “0” отражает тот факт, что на кристалл не наложено поле.

При наложении электрического поля E = {E_x; E_y; E_z} уравнение индикатрисы принимает вид:

(7)

где коэффициенты a_ijзависят от поля следующим образом: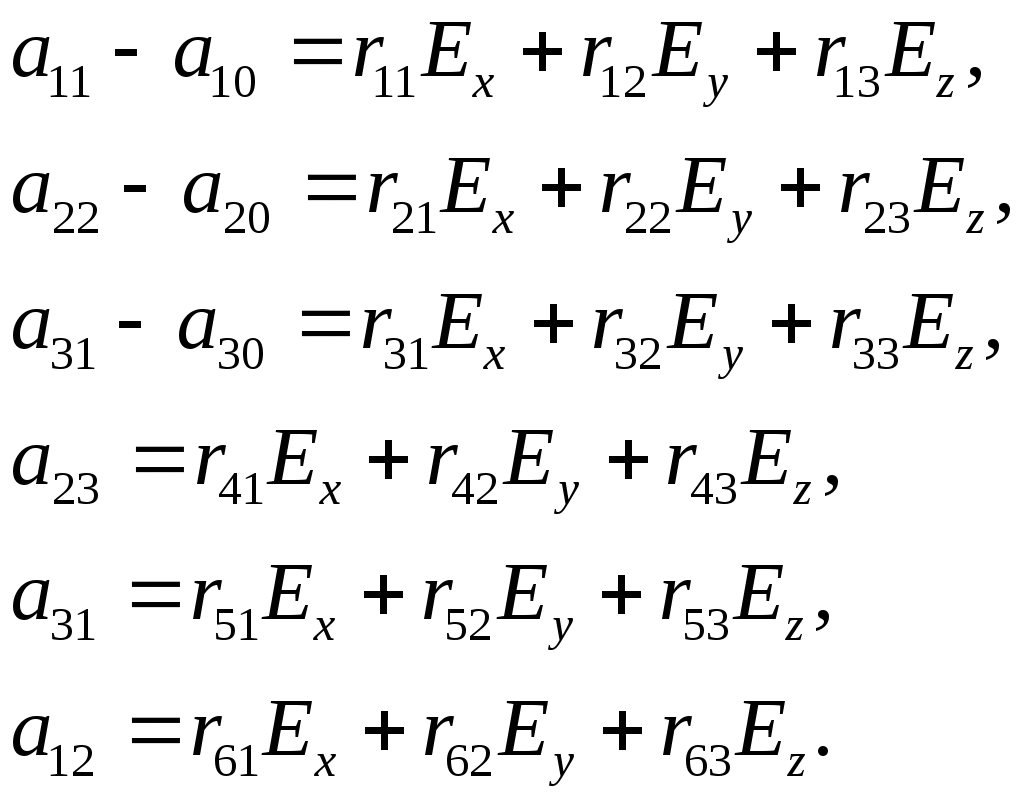

(8)

Коэффициенты r_ij называются электрооптическими коэффициентами, максимальное число их равно 18, однако число отличных от нуля и число независимых электрооптических постоянных значительно меньше и определяется симметрией кристалла.

Рассмотрим электрооптический эффект в кристалле ниобата лития. Это одноосный кристалл (a₁₀ = a₂₀), у которого отличны от нуля следующие электрооптические коэффициенты: r₁₃ = r₂₃; r₃₃; r₄₂ = – r₅₁; r₂₂ = – r₁₂ = – r₆₁ . Уравнение оптической индикатрисы для ниобата лития при произвольном направлении электрического поля имеет вид:

(9)

Видно, что при наличии электрического поля оси эллипсоида x^’, y^’, z^’ не совпадают с исходными кристаллографическими осями x, y, z. Для того, чтобы найти новые направления осей, необходимо привести (9) к каноническому виду.

Рассмотрим наиболее интересный в практическом отношении случай. Пусть электрическое поле перпендикулярно оптической оси z, т.е. E_z = 0; E_y ¹0; E_x ¹0. В этом случае уравнение индикатрисы принимает вид:

(10)

Если свет распространяется вдоль оптической оси кристалла (случай, когда поле приложено перпендикулярно направлению распространения света, называется поперечным электрооптическим эффектом), то для нахождения главных показателей преломления необходимо рассмотреть сечение оптической индикатрисы плоскостью, перпендикулярной z. Это сечение является эллипсом, удовлетворяющим уравнению:

(11)

Главные оси эллипса x^’, y^’повернуты на угол a относительно кристаллографических осей x, y, причем

(12)

В главных осях уравнение эллипса (11) запишется в виде: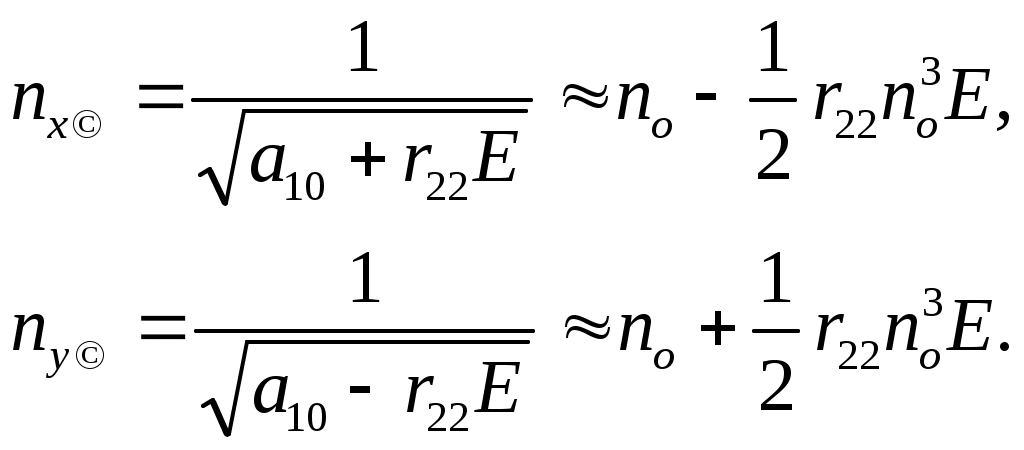

(13)

где . Т.о., показатели преломления для света, поляризованного в главных направлениях, равны:

(14)

Тогда, согласно (5), разность фаз между волнами после прохождения пластинки толщиной l равна:

(15)

где U – приложенное напряжение; d – размеры кристалла вдоль поля. Следует отметить, что если свет распространяется не точно по оптической оси, то в (15) появляется начальный сдвиг фаз

(16)

обусловленный естественной, не связанной с полем анизотропией. Индекс “е” вверху означает текущее (при произвольном угле между волной и оптической осью) значение показателя преломления для необыкновенной волны, которое может изменяться от n_oдо n_e.
1.3. Статическая модуляционная характеристика электрооптического модулятора
Как уже указывалось, если на кристаллическую пластинку падает линейно поляризованный свет, то на выходе ее получается свет эллиптически поляризованный в общем случае. Прикладывая электрическое поле к кристаллу, мы меняем форму и ориентацию эллипса, т.е. осуществляем модуляцию света по поляризации, но интенсивность света остается неизменной. Для получения модуляции интенсивности света необходимо кристалл поместить между поляризатором и анализатором, как это показано на рис.3. Если анализатор скрещен с поляризатором, то интенсивность на выходе такого модулятора равна:

(17)

где I₀ – максимальная интенсивность проходящего света.




Рис. 3



Рис. 4
Зависимость интенсивности света от статического напряжения U изображена на рис.4. Для изменения интенсивности света от нуля до максимального значения необходимо приложить к кристаллу напряжение U_l/2 . Это напряжение называется полуволновым , т.к. разность хода между обыкновенной и необыкновенной волнами в этом случае равна l/2. Из (15) нетрудно определить связь между полуволновым напряжением и параметрами кристалла:

(18)
При другой конфигурации поля и осей кристалла аналогичные формулы, естественно, будут иметь иной вид.

2. Описание установки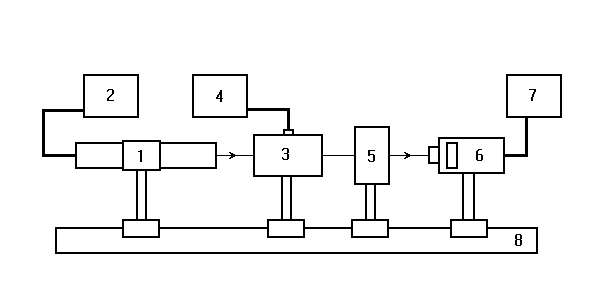



Рис. 5. Схема лабораторной установки

Лабораторная установка (рис.5) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), электрооптического модулятора МЛ-5 (3) на основе кристалла LiNbO₃, источника питания модулятора (4), анализатора (5), фотоприемника (6) с цифровым индикатором и блоком питания (7). Все оптические элементы размещены на оптической скамье (8). Показания цифрового индикатора фотоприемника (фототок) пропорциональны интенсивности света, падающего на фотоприемник. Излучение лазера линейно поляризовано. Поляризатор лазера (1), модулятор (3) и анализатор (5) образуют так называемую ячейку Поккельса, позволяющую осуществлять амплитудную модуляцию прошедшего через нее света с помощью прикладываемого к модулятору напряжения от источника питания (4).

ВНИМАНИЕ ! В работе используется высокое напряжение (до 600 В). Электрооптический модулятор электрически уже соединен со своим источником питания. Студентам самостоятельно подключать или отключать разъемы модулятора и источника питания ЗАПРЕЩАЕТСЯ.

3. Порядок выполнения работы
3.1. Включить источник питания лазера и блок питания фотоприемника.
3.2. Съюстировать при необходимости все оптические элементы по лучу лазера так, чтобы луч проходил через центр всех элементов нормально к рабочим поверхностям этих элементов. Это можно проконтролировать по отражению: отраженный луч должен попадать в выходное отверстие лазера.
3.3. Перекрыв лазерное излучение возле самого лазера, измерить темновой ток. В дальнейшем из показаний фотоприемника необходимо вычитать это значение.

3.4. Вращая оправу анализатора, определить такое положение, когда плоскость пропускания анализатора будет перпендикулярна плоскости поляризации падающего на анализатор лазерного излучения (по минимуму показаний фотоприемника).
3.5. Установить регулятор напряжения на источнике питания модулятора в крайнее левое положение. Включить источник питания модулятора.
3.6. Изменяя выходное напряжение U источника питания модулятора, снять зависимость показаний фотоприемника I от напряжения U через 20 В до 500 В (в области экстремумов зависимости – через 10 В). Измерения повторить не менее пяти раз.
3.7. Перевести регулятор напряжения на источнике питания модулятора в крайнее левое положение. Выключить все приборы.

3.8. Построить экспериментальную зависимость (где I^/= (I – I_min), I₀^/= (I₀ – I_min), I₀ – показания фотоприемника в максимуме пропускания ячейки Поккельса, I_min – показания фотоприемника в минимуме) с учетом статистической обработки результатов с доверительной вероятностью 90%.
3.9. Используя определение полуволнового напряжения U_l/2, определить его значение из полученного графика.
3.10. По формуле: (19)

где n₀ =2,2884 – обыкновенный показатель преломления кристалла; n_е =2,2019 – необыкновенный показатель преломления кристалла; l – длина волны излучения лазера; r₃₃=32,2×10^-12 м/В; r₁₃=10×10^-12 м/В – электрооптические коэффици­енты; d = 3 мм – толщина кристалла (расстояние между обкладками вдоль приложенного внешнего поля); l = 40 мм – длина кристалла вдоль направления луча, найти расчетное значение полуволнового напряжения для данного модулятора.
3.11. Используя полученное из эксперимента значение полуволнового напряжения, построить зависимость пропускания ячейки Поккельса от приложенного напряжения U по формуле:

(20)

в одной координатной плоскости с экспериментальным графиком п. 3.8.
3.12. Сравнить полученные расчетные результаты с экспериментальными.

4. Контрольные вопросы и задания

1. 
   Что называется оптической осью анизотропной среды? Какую поляризацию может иметь свет, распространяющийся вдоль оптической оси?
   
2. 
   Сколько оптических осей может существовать в кристалле? Что такое одноосные и двуосные кристаллы?
   
3. 
   Дайте характеристику взаимного расположения векторов электромагнитного поля для плоской волны в кристалле.
   
4. 
   Дайте определение обыкновенной и необыкновенной волны. Как соотносятся между собой показатели преломления этих волн?
   
5. 
   Что такое оптическая индикатриса кристалла? Какие характеристики можно определить с ее помощью?
   
6. 
   В чем заключаются электрооптические эффекты Керра и Поккельса? Чем они отличаются?
   
7. 
   Дайте определение полуволнового напряжения. Какие параметры влияют на его величину и какой физический смысл оно имеет?
   
8. 
   Выведите формулу (19). Какой конфигурации внешнего электрического поля и осей кристалла она соответствует?
   
9. 
   Ячейку Керра с нитробензолом поместили между двумя скрещенными поляризаторами так, что направление электрического поля Е в конденсаторе образует угол 45⁰ с плоскостями пропускания поляризаторов. Конденсатор имеет длину l=100 мм. Через систему проходит свет с l=0,5 мкм. Имея в виду, что здесь постоянная Керра B = 2,2×10^-10 см/В² , определите число прерываний света в 1 с, если на конденсатор подать синусоидальное напряжение с частотой 10 МГц и амплитудой напряженности E_m = 50 кВ/см. Постоянной Керра называется коэффициент B в формуле .
   
10. 
    Предложите, где на практике можно использовать электрооптический эффект.
    

Лабораторная работа

ЗАКОН МАЛЮСА
ЦЕЛЬ РАБОТЫ: ознакомление с методами получения и анализа линейно поляризованного света, работой простейших поляризационных устройств.
ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, поляризатор с лимбом, фотоприемник, оптическая скамья.
1. Теоретическая часть
Представление о поляризации света как его особом физическом свойстве впервые ввел И.Ньютон в 1704 г. Сам термин “поляризация” принадлежит французскому инженеру и физику Э.Малюсу (1775–1812). Световые волны, у которых направления колебаний векторов электрического E и магнитного H полей сохраняются неизменными в пространстве или изменяются по определенному закону, называются поляризованными.
1.1. Виды поляризации световых волн
Если вектор E световой волны колеблется лишь в одной неизменной в пространстве плоскости, то такая волна называется линейно или плоско поляризованной. При линейной поляризации плоскость, содержащая волновой вектор k и вектор E, называется плоскостью колебаний или плоскостью поляризации волны.

Если же колебания вектора E совершаются так, что его конец описывает окружность в плоскости, перпендикулярной направлению распространения волны k, то такая волна называется поляризованной по кругу, еслиэллипс, то эллиптически поляризованной.

Световая волна, в которой различные направления вектора E в поперечной к направлению распространения волны плоскости равновероятны, называется естественной (естественно поляризованной или неполяризованной).
1.2. Суперпозиция двух линейно поляризованных волн [2]
Рассмотрим суперпозицию двух линейно поляризованных волн с одинаковыми частотами w, амплитудами электрических полей E₁ и E₂, распространяющихся в одном направлении (вдоль оси Z декартовой системы координат) со сдвигом фаз d. Пусть вектор E₁ колеблется в плоскости XZ, а вектор E₂ – в плоскости YZ: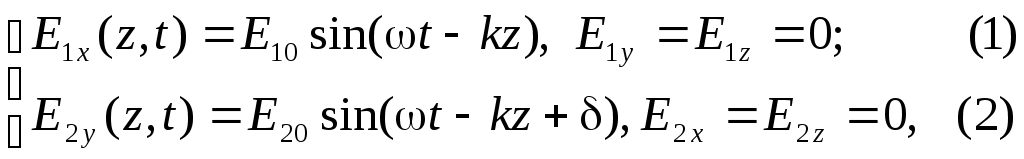



Найдем состояние поляризации суммарной волны, определяемой суперпозицией полей E ={E_x; E_y; E_z}= E₁+E₂, складывая покоординатно поля (1) и (2). Перепишем (2) в виде:

(3)

Исключая в (3) с помощью (1) 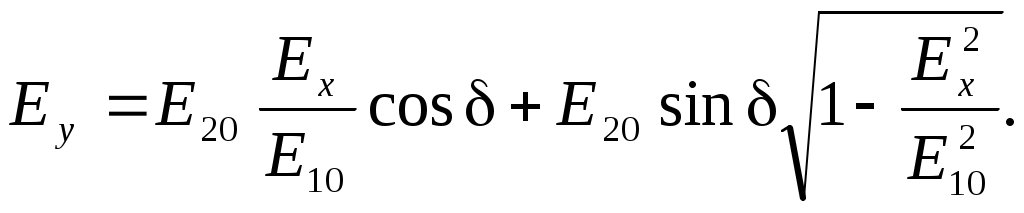и , получаем:

(4)

После перегруппировки получаем окончательно уравнение, описывающее состояние поляризации суммарного поля в общем виде: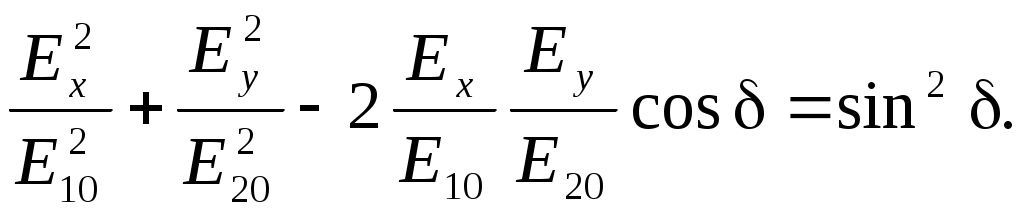

(5)
Рассмотрим основные случаи состояния поляризации. Если 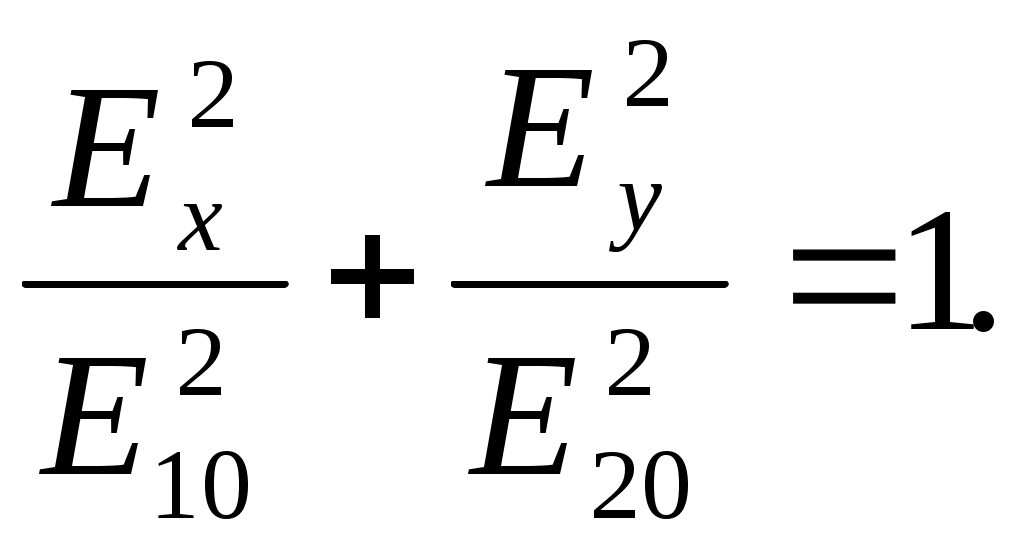, то уравнение (5) принимает вид:

(6)




Рис. 1
При это выражение является уравнением эллипса с центром в начале системы координат и осями, направленными вдоль осей X и Y (рис.1). Поляризация при этом называется эллиптической. Если при наблюдении навстречу волне вращение вектора E в фиксированной плоскости (перпендикулярной волновому вектору) происходит по часовой стрелке, то такая волна называется правой эллиптически поляризованной волной, если против часовой стрелки – левой эллиптически поляризованной волной.

Если , то эллипс вырождается в окружность. Такая поляризация называется круговой или циркулярной. Понятия правой и левой круговой поляризации применимы здесь аналогично определенным выше для эллиптической поляризации.




Рис. 2
При (общий случай выражения (5)) поляризация является также эллиптической, главные оси эллипса не совпадают с осями координат (рис.2). Ориентация эллипса зависит от сдвига фаз d. При этом эллиптичность поляризации остается и при .

При уравнение (5) описывает прямые:
(7)



Рис. 3

Конец суммарного вектора электрического поля движется вдоль соответствующего отрезка прямой (7) (рис.3). Получаемая линейно поляризованная волнаявляется предельным случаем эллиптически поляризованной волны.

Видно, что световая волна с любой поляризацией может быть представлена в виде суперпозиции двух линейно поляризованных во взаимно-перпендикулярных плоскостях волн. Поэтому можно сказать, что электромагнитные волны обладают двумя независимыми состояниями поляризации.
1.3. Методы получения линейно поляризованного света [9]
Излучение обычных (тепловых) источников света не поляризовано. В этом случае совокупность огромного числа элементарных источников (атомов или молекул) испускают свет независимо друг от друга с разными фазами и с разными ориентациями векторов электромагнитного поля E и H. Поэтому их ориентация в результирующей волне хаотически изменяется со временем, так что все направления оказываются равновероятными.

Для получения линейно поляризованного света применяются специальные оптические приспособления – поляризаторы. Принципы их действия и конкретные устройства могут быть различными, но общим является то, что при падении света с любым типом поляризации (в т.ч. и неполяризованного) на поляризатор на выходе свет имеет линейную поляризацию. Плоскость колебаний электрического вектора в волне, прошедшей через поляризатор, называется плоскостью поляризатора. Всякий поляризатор можно использовать и для исследования поляризованного света, т.е. в качестве анализатора.

Опишем некоторые способы получения линейно поляризованного света.

а) Отражение света от поверхности диэлектрика. Отраженный от диэлектрика свет всегда частично поляризован из-за различия коэффициентов отражения для двух волн с независимыми поляризациями (различают случаи, когда вектор E в падающей волне или лежит в плоскости падения (p–поляризация) или перпендикулярен ей (s–поляризация)). Состояние поляризации отраженной волны зависит от относительного показателя преломления n и от угла падения a (подробнее см. лабораторную работу “Отражение и преломление света на границе двух сред”). При падении произвольно поляризованной волны на границу раздела под углом Брюстера a_Б отраженная волна линейно поляризована и имеет s–поляризацию. P–поляризованная волна полностью проходит во вторую среду и не отражается.