лабораторный практикум. Практикум волгоград 2014 Печатается по решению редакционноиздательского совета

• Название: Практикум волгоград 2014 Печатается по решению редакционноиздательского совета
• Анкор: лабораторный практикум
• Дата: 26.04.2023
• Размер: 5.21 Mb.
• Имя файла: LABORATORNAYa.doc
• Тип: Практикум; #1091404
• страница: 3 из 9

1.2. Закон Бугера

Рассмотрим поглощение света модельной средой, представляющей собой ансамбль гармонических осцилляторов (атомов в единице объёма). Пусть плоская монохроматическая световая волна проходит отрезок длиной dz, причём среда содержит N элементарных осцилляторов (атомов в единице объёма). Обозначив площадь поперечного сечения светового пучка S, запишем полное число осцилляторов, находящихся в поле световой волны в виде
dN=NSdz. (21)
Будем считать, что каждый осциллятор поглощает мощность P₀. Тогда суммарное изменение мощности света на данном отрезке среды составит
dP= –P₀ dN. (22)

Соответственно, изменение интенсивности света будет равно

dI= –SdP= –P₀ Ndz. (23)

Подставив сюда выражение для P₀, получаем уравнение для интенсивности света: dI= –IαΝdz, (24)

решение которого: I(z)=I₀ exp(–αz), (25)

где I₀ – интенсивность падающей волны, α– показатель поглощения.

Это соотношение отражает закон поглощения света в среде, называемый также законом Бугера – Ламберта – Бэра. Согласно этому закону, интенсивность света экспоненциально уменьшается по мере увеличения расстояния, пройденного светом в среде.

Показатель поглощения α не зависит ни от интенсивности падающего света, ни от геометрических размеров облучаемого образца, а является характеристикой самого поглощающего материала. Для разных веществ, в разных условиях коэффициент поглощения света меняется в широких пределах. Например, для оптических волокон α=10^-4-10^-6 см^-1, а для металлов и полупроводников α=10³-10⁶ см^–1. Наряду с показателем преломления, показатель поглощения является важнейшей оптической характеристикой вещества.

Мы вывели закон Бугера исходя из простейшей модели среды как ансамбля неподвижных невзаимодействующих между собой классических осцилляторов. Однако экспериментальные исследования показывают, что этот закон справедлив для широкого класса объектов: жидких, твёрдых, газообразных сред, а также смесей различных веществ. Отклонения от этого закона начинают проявляться лишь при воздействие на вещество очень мощных (лазерных) световых пучков. Эти отклонения связаны с нелинейностью отклика вещества на сильное световое поле, квантовыми эффектами и т.д.

2. Описание установки

Лабораторная установка (рис.3) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), набора плоскопараллельных пластин (3), фотоприемника (4) с цифровым индикатором и блоком питания (5). Все оптические элементы размещены на оптической скамье (6). Показания цифрового индикатора фотоприемника (фототок) пропорциональны интенсивности света, падающего на фотоприемник.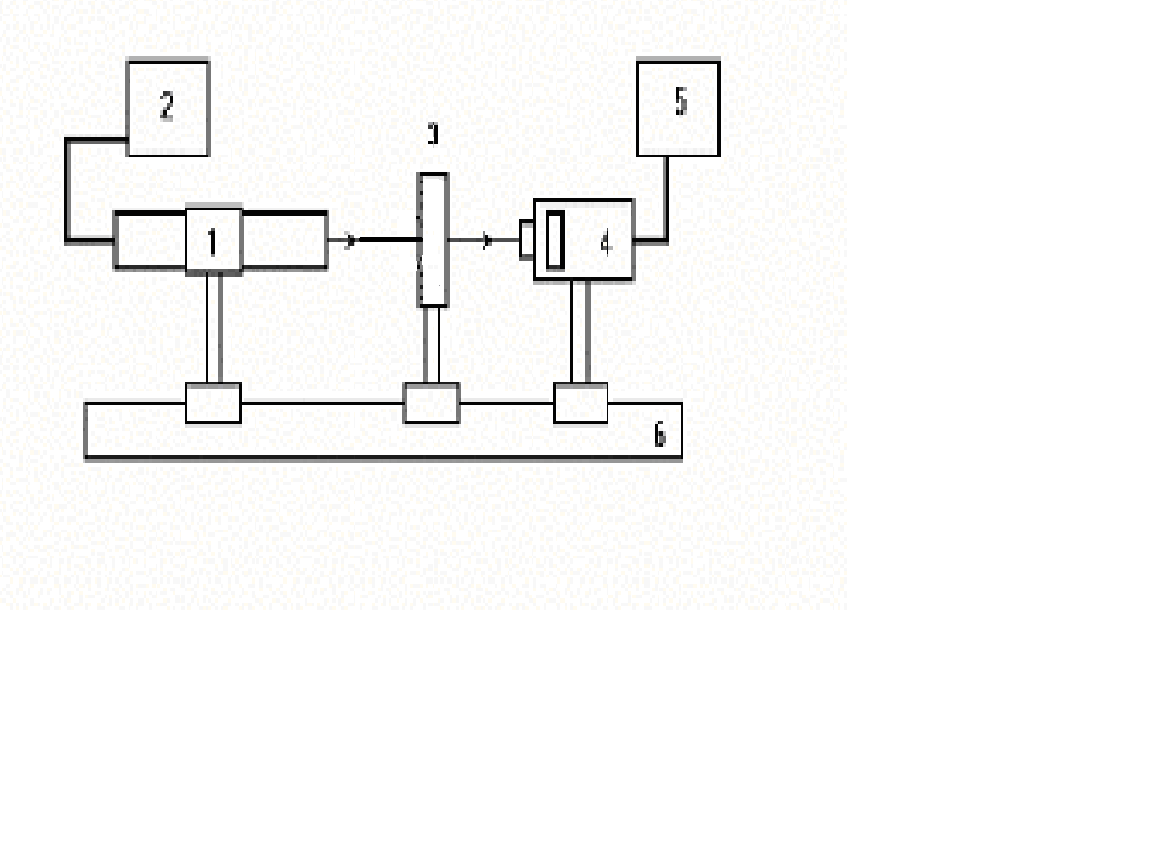



Рис.3. Схема лабораторной установки
3. Порядок выполнения работы

3.1. Включить источник питания лазера и блок питания фотоприемника.

3.2. Съюстировать при необходимости все оптические элементы по лучу лазера так, чтобы луч проходил через центр всех элементов нормально к их рабочим поверхностям. Это можно проконтролировать по отражению: отраженный луч должен попадать в выходное отверстие лазера.

3.3. Перекрыв лазерное излучение возле самого лазера, измерить темновой ток. В дальнейшем из показаний фотоприемника необходимо вычитать это значение.

3.4. Направить излучение лазера на фотоприемник и измерить значение фототока I₀ в отсутствие поглотителей (z=0).

3.5. Постепенно увеличивая толщину поглощающего слоя zпутем введения в поток излучения все большего числа поглотителей, снять значения фототока I(z), соответствующие текущим толщинам поглощающего слоя.

3.6. Повторить п.3.5. пять раз, сохраняя последовательность введения поглотителей. Вычислить I_ср(z).

3.7. Учесть темновой ток и потери на отражение от поверхности поглотителей. Измеренное значение фототока I_эксп (z)= [I_ср(z) – I_темн] / (1 – R) ^β,

где R=[(n-1)/(n+1)]² – энергетический коэффициент отражения при нормальном падении света; n=1.5 – коэффициент преломления стекла, β - число, равное количеству отражающих поверхностей.

3.8. Построить зависимость ln{I₀ / I_эксп(z)}, аппроксимировать её прямой по методу наименьших квадратов. Вычислить коэффициент поглощения α как тангенс угла наклона полученной прямой к оси z.

3.9. На одной координатной плоскости построить графики экспериментальной I_эксп(z) / I₀ и теоретической exp {–αz} зависимостей.

3.10. Провести статистическую обработку результатов с доверительной вероятностью 90%. Отметить погрешности на экспериментальной зависимости. Занести результаты в таблицу 1.

Таблица 1. Экспериментальная I_эксп(z) / I₀ и теоретическая exp {–αz} зависимости интенсивности излучения, прошедшего через поглощающий слой толщиной z.

Z,мм	I1	I2	I3	I4	I5	Iср(z), Вт/м2	Iэксп(z)/I0	Iэксп (z) Вт/м2	Iэксп(z) Вт/м2	exp{–αz}

4. 
   Контрольные вопросы и задания
   

1. 
   Исходя из формулы (10) получить выражение (14) для комплексного показателя преломления.
   
2. 
   Как изменится интенсивность света, прошедшего через пластинку толщиной z при изменении частоты падающего излучения.
   
3. 
   Найти коэффициент отражения от поглощающего вещества, показатель преломления которого равен . Свет падает на вещество нормально.
   
4. 
   Найти «глубину проникновения» света в поглощающее вещество при нормальном падении. Показатель преломления вещества (). За глубину проникновения принять расстояние, на котором интенсивность уменьшается в е раз.
   
5. 
   Описать качественно зависимость глубины проникновения от частоты падающего света, если для () и () справедлива формула (20).
   
6. 
   Как изменяется отражательная способность (отношение интенсивности отраженного света к интенсивности падающего) при увеличении ()? Когда происходит увеличение () и по какой причине? Падение света нормальное.
   
7. 
   Может ли показатель преломления быть меньше единицы?
   
8. 
   Радиоволна распространяется вверх. Волны каких частот могут проходить через ионосферу? Какие волны будут полностью отражаться?
   
9. 
   Радиосигнал определенной частоты  посылается вверх и отражается на определенной высоте. Определить концентрацию электронов в точке отражения.
   
10. 
    Объясните происхождение «блеска» металлов. Какой металл «блестит» сильнее – Au или Ag? Показатели преломления для этих металлов соответственно равны .
    
11. 
    Описать качественно, почему возможно использование излучения СО₂ лазера (=10.6 мкм) для резки стекла и керамики?
    
12. 
    Пользуясь выражением для () объяснить качественно, по какой причине и как изменяется показатель преломления воздуха при увеличении высоты над поверхностью Земли. К каким оптическим эффектам в атмосфере приводит такое изменение?
    
13. 
    Изменяется ли с высотой величина для атмосферного воздуха?
    
14. 
    Пользуясь формулами (14) и (15), опишите, как и почему возможно использование спектрофотометра для целей спектрального анализа.
    
15. 
    Объясните принцип действия фильтров: красного, синего, зеленого.
    
16. 
    Показатель преломления германия для ₀=0.5 мкм (в вакууме) определяется выражением . Чему равен коэффициент отражения от полированной поверхности германия при нормальном падении?
    
17. 
    Рассчитать для германия ( ) для λ₀=0.5 мкм (в вакууме) фазовый сдвиг, возникающий при отражении, для случая нормального падении.
    
18. 
    Чему равна глубина проникновения плоской волны в германий?
    

Лабораторная работа

ИССЛЕДОВАНИЕ ОПТИЧЕСКОЙ АКТИВНОСТИ
ЦЕЛЬ РАБОТЫ - ознакомление с экспериментальным методом исследования веществ, обладающих способностью вращать плоскость поляризации проходящего через них излучения.

ПРИНАДЛЕЖНОСТИ - монохроматор, кювета с исследуемым раствором, поляризатор, ртутная лампа, осветитель.
I. Теоретическая часть.

Электромагнитные волны, в частности световые, у которых направления колебаний электрического и магнитного полей сохраняются неизменными либо испытывают закономерные изменения ориентации (вращаются), - называются поляризованными. В этом случае для волн видимого диапазона употребляется термин поляризованный свет. К числу излучателей, испускающих поляризованный свет, относятся, например, возбужденные газы или пары, помещенные в магнитное поле. У таких источников света спектральные линии излучения поляризованы. Можно получить поляризованный свет и из естественного с помощью различных приборов (например, призмы Николя или поляроидов). В поляризованном свете плоскость, параллельная направлению колебаний вектора Е и направлению распространения волны (направление волнового вектора k), называется плоскостью поляризации.
1.1. Оптическая активность

Вещества, обладающие способностью вращать плоскость поляризации, называются оптически активными. Опыт показывает, что угол поворота плоскости поляризации прямо пропорционален толщине вращающего слоя d:

=d , (1)

где  - некоторая характерная для каждого оптически активного вещества постоянная. Например, для кварца для длины волны =5890 A (желтая линия в спектре испускания натрия) величина  =21.7 град/мм

Наряду с твердыми телами, способностью вращать плоскость поляризации обладают растворы некоторых веществ. Вращательная способность растворов прямо пропорциональна толщине слоя раствора и его концентрации (закон Био):

=dс (2)

где  - постоянная вращения, d - толщина слоя, с - концентрация раствора. Из формулы (2) следует, что если известна величина , то, измеряя при данной толщине слоя d угол поворота плоскости поляризации , можно измерить концентрацию вещества в растворе. На этом принципе основано действие соответствующих приборов (например, сахариметров).
1.2. Теоретическое описание вращения плоскости поляризации

Френель, изучая оптически активные вещества, высказал предположение, что в этих веществах возбуждаются волны, поляризованные по кругу. Т.е. структура этих веществ допускает существование в них волн круговой поляризации в качестве так называемых нормальных (или собственных) волн. Свое предположение Френель доказал при помощи специально созданной системы призм. При этом важным является предположение о том, что скорости волн, поляризованных по правому и левому кругу, являются различными.

Рассмотрим прохождение плоской линейно-поляризованной волны через оптически активное вещество. Предположим, что вектор электрического поля падающей волны направлен вдоль оси Х. Ось Z направим по вектору m, указывающему направление распространения волны. Таким образом, падающая на оптически активное вещество волна имеет компоненты: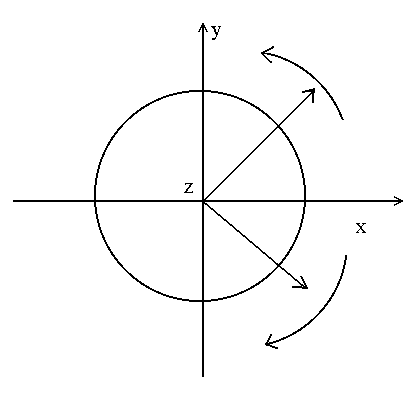


Рис. 1
(3)

Падающая линейно поляризованная волна возбуждает в веществе две волны, поляризованные по кругу. При этом на границе среды

(4)

здесь , - амплитуды волн, поляризованных соответственно по пра­вому и левому кругу; 2Е - амплитуда падающей линейно поляризованной волны.

Для каждой волны после прохождения расстояния d в оптически активной среде можно записать: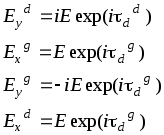

, (5)

где фаза волны . (6)

Здесь учтен тот факт, что для волны, поляризованной по кругу

, (7)

где знак (+) берется для волны, поляризованной по право­му кругу, а знак (–) - для волны, поляризованной по левому кругу. Волна на выходе будет иметь компоненты:





Для определения характера поляризации выходящей волны найдем отношение компонентE_y/E_x: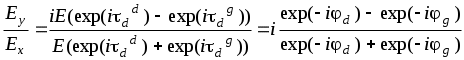


где

Далее

Здесь (8)

После проведения несложных преобразований получаем:

(9)

Из последнего выражения следует два важных результата.

1. Поскольку отношение вещественно, то выходящая волна поляризована линейно.

2. По смыслу отношение есть тангенс угла, образуемого на­правлением колебаний линейно поляризованного света с осью X, т.е , или для малых углов .

В нашем случае угол как раз характеризует угол поворота плоскости поляризации, поскольку по условию в начальный момент времени вектор напряжённости электрического поля Е направлен вдоль оси X. Следовательно, угол поворота плоскости поляризации линейно поляризованной волны после прохождения оптически активного вещества толщиной d оп­ределяется выражением (10)

Таким образом, в рамках макроскопической электромагнитной тео­рии света вращение плоскости поляризации получило объяснение. Однако, эта теория не может объяснить, почему скорость волны в правовращающем веществе отлична от скорости в левовращающем.

С позиций молекулярной теории вращение плоскости поляризации связано с асимметрией строения оптически активного вещества. Этот вопрос был исследован М. Борном, рассмотревшим сложные асимметричные молекулы с пространственной структурой, не имеющие ни центра симмет­рии, ни плоскости симметрии.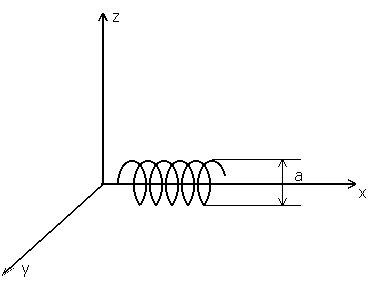

Наиболее простая модель этой молекулы – отрезок спирали. Пусть на такую молекулу, диаметр витка которой равен а, падает линейно поляризованная волна (рис.2). Она вызовет движение зарядов, направленное вдоль оси Х. Но если заряды будут двигаться вдоль спирали, то неизбежно возникнет их движение вдоль оси Y. Возникающее движение зарядов приведет к возбуждению Y - компоненты волны в Рис. 2

веществе, наличие которой должно привести к отклонению плоскости колебаний от направления Е=Е_х Детальный расчет приводит к следующему результату для разности показателей преломле­ния:

(11)

здесь - некоторая постоянная, l - характерный размер молекулы оптически активного вещества. Таким образом, молекулярная теория позволяет объяснить различие в скоростях распространения волн, по­ляризованных по правому и левому кругу, что является существенным моментом в объяснении явления вращения плоскости поляризации.
2.Описание установки.

Лабораторная установка (рис. 3) состоит из монохроматора (1), ртутной лампы (2), предназначенной для градуировки монохроматора, пульта питания (3), двух окулярных насадок к монохроматору - с ножом (4) и со щелью (5). Первая используется при градуировке, вторая - при измерениях.
Рис. 3. Схема лабораторной установки

О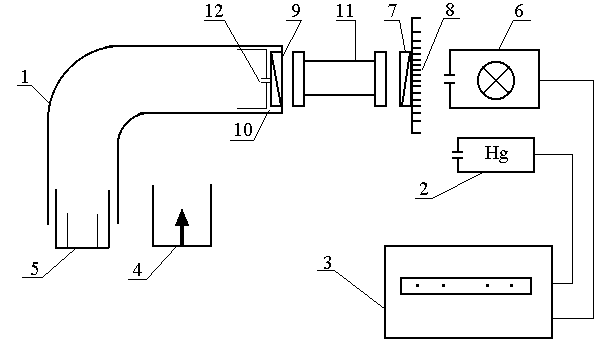
светитель (6) служит источником сплошного спектра. На нем укреплен вращающийся поляризатор (7) с лимбом и нониусом (8). Анализатор (9) вмонтирован во входное окно (10) монохроматора. Он неподвижен. Исследуемый раствор находится в кювете (11). При градуировке входная щель (12) монохроматора должна быть предельно малой (0.01 - 0.02 мм); при работе - полностью открытой. Для уменьшения фоновой засветки раствора желательно, чтобы оптические оси источника света, кюветы и входной трубы монохроматора совпадали. Однако, в процессе работы переюстировка запрещается.

3. Порядок выполнения работы

В настоящей работе исследуется вращение плоскости поляризации раствором активного вещества (сахарозы С₁₂Н₂₂О₁₁ в оптически нейт­ральном растворителе).

3.1. Используя формулу 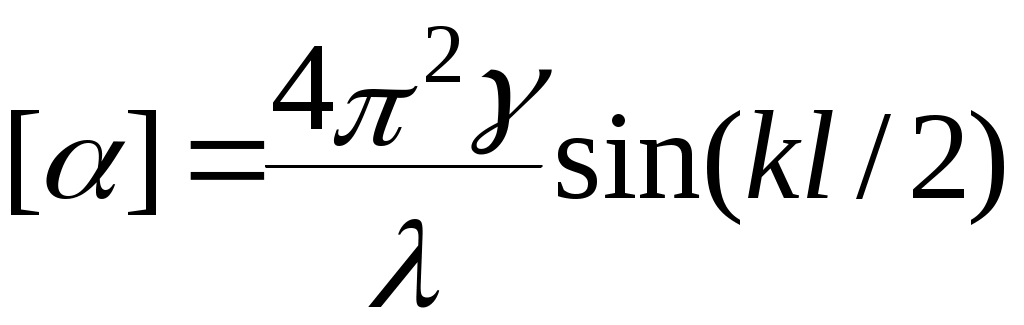построить теоретическую зависимость постоянной врашения от длины волны для видимой области спектра в диапазоне от 400 Ả до 800 Ả с интервалом 25 Ả, полагая l = 10 Ả, = 0.019 град·см²/г. Построение выполнить заранее в процессе домашней подго­товки к работе.
3.2. Произвести градуировку монохроматора. Для этого:

3.2.1. Установить ртутную лампу на рельсе и совместить оптические оси источника излучения и входной трубы монохроматора. Для увеличения интенсивности спектра поместить между ртутной лампой и монохроматором конденсор.

3.2.2. Добиться четкого изображения источника в центре колпачка на входной трубе, меняя положение лампы и конденсора на рельсе.

3.2.3. Укрепить на спектроскопе окулярную насадку с ножом.

3.2.4. Навести окуляр на резкость по ножу.

3.2.5. Ориентируясь на желтый дублет ртути (5770 Ả и 5790 Ả), отож­дествить ртутный спектр с указанным в атласе.

3.2.6. Произвести градуировку прибора (снять зависимость между пока­заниями барабана и длиной волны для каждой наблюдаемой линии ртутного спектра), взять не менее 25 точек во всех областях видимого спек­тра.

3.2.7. Построить градуировочный график.

3.3. Используя метод скрещенных поляризаторов, получить зави­симость угла поворота плоскости поляризации от длины волны излучения _.

3.3.1. Заменить ртутную лампу источником сплошного спектра.

3.3.2. Совместить оптические оси входной трубы монохроматора и ос­ветителя.

3.3.3. Укрепить на монохроматоре окулярную насадку со щелью.

3.3.4. Вращением поляризатора добиться минимального значения интенсивности, при этом от­счет по лимбу поляризатора принять за нулевой.

3.3.5. Установить между поляроидами кювету с исследуемым раствором.

3.3.6. Вращая поляризатор, добиться вновь минимального значения интенсивности для последовательных положений барабана монохроматора с шагом, соответствующим изменению длины волны излучения на 50 Ả За угол поворота плоскости поляризации φ принять разницу положений поляризатора (по лимбу).
3.4. Пересчитать зависимость по формуле

при d= 20 см, c= 0.87 г/см³.

3.5. Провести статистическую обработку результатов с доверительной вероятностью 90%.

3.6. На одной координатной сетке построить экспериментальные и теоретические зависимости постоянной вращения от длины волны и _.
4. Контрольные вопросы и задания

1. В чем отличие поляризованного света от неполяризованного ?

2. Как отличить свет, поляризованный по кругу, от естественного света ?

3. Описать характер поляризации плоской монохроматической световой волны в зависимости от отношения компонент комплексной амплитуды - электрического поля волны.

4. Описать установку, предложенную Френелем для экспериментального доказательства существования в одной из модификаций кристалла кварца двух циркулярно поляризованных волн.

5. Дать свои соображения относительно прямо пропорциональной зависимости угла поворота плоскости поляризации в растворах оптически активных веществ от концентрации последних.

6. Рассмотреть случай, когда падающий на активное вещество линейно поляризованный свет направлен под углом 45° к оси Х. Провести анализ вращения плоскости поляризации.

7. Пластинка кварца толщиной в 1 мм вырезана перпендикулярно к оптической оси и помещена между скрещенными николями. Будет ли пластинка оставаться освещенной при любой, длине волны падающего света из видимого диапазона? Объясните возникающее явление.

8. Какую минимальную разность показателей преломления право- и левополяризованных по кругу волн ( = 5893 А°) можно обнаружить при слое вещества l = 30 см, если измерять угол поворота плоскости поля­ризации с точностью 1° ?

9. Объяснить действие поляризационной призмы Николя. Определить степень поляризации выходящего из призмы излучения при падении на нее естественного света.

10. Сравните действие поляроидной пластинки на поляризованное излу­чение маломощного непрерывного лазера и на естественный свет (в пос­леднем случае для контроля поляризации применить два скре­щенных поляроида).

11. Оценить степень поляризации прошедшего света, отраженного под углом Брюстера от стеклянной пластинки. Падающий свет – естественный.

12. Ветровое стекло и фары автомашины иногда снабжаются пластинками из поляроида. Как должны быть расположены эти пластины, чтобы шофер мог видеть дорогу, освещенную светом его фар, и не страдал от света фар встречных машин? Возможна ли, ситуация, когда при включенных фарах машин водители не увидят машину, едущую навстречу, и произойдет автомобильная катастрофа? Объяснение дать на основании законов оптики.