лабораторный практикум. Практикум волгоград 2014 Печатается по решению редакционноиздательского совета
 Скачать 5.21 Mb. Скачать 5.21 Mb.
|
|
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА НА ГРАНИЦЕ ДВУХ СРЕД Лабораторная работа ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ СВЕТА НА ГРАНИЦЕ ДВУХ СРЕД (ФОРМУЛЫ ФРЕНЕЛЯ) ЦЕЛЬ РАБОТЫ: Изучение законов и исследование отражения и прохождения световых электромагнитных волн (ЭМВ) на границе раздела двух сред; анализ амплитудных и энергетических коэффициентов отражения и пропускания ЭМВ на этой границе; освоение методов юстировки оптических систем с использованием лазера. ПРИНАДЛЕЖНОСТИ: оптическая скамья, маломощный непрерывный лазер, диафрагма, стеклянная плоскопараллельная пластина, укрепленная на лимбе, фотоприемник. Теоретическая часть Электромагнитная волна, падая на границу раздела двух сред, частично отражается от поверхности раздела и частично преломляется, переходя во вторую среду. Физические явления, имеющие место в этом случае, следует прежде всего охарактеризовать энергетически, вводя понятие коэффициентов отражения и пропускания. Но необходимо исследовать и фазовые соотношения на границе двух сред. Это позволит получить новую информацию об изучаемых физических явлениях. 1.1. Законы отражения и преломления электромагнитных волн Граничные условия для векторов поля световой волны на границе между двумя диэлектриками при отсутствии свободных зарядов и токов проводимости имеют вид: где t, n – индексы тангенциальных (касательных к границе раздела) и нормальных компонент векторов соответственно. Пусть на плоскую границу двух диэлектриков с абсолютными (не относительными!) проницаемостями (e1 ; m1) и (e2 ; m2) (магнитную проницаемость пока оставим в общем виде) падает под некоторым углом плоская световая волна (рис.1). Тогда для напряженностей электрического поля в падающей, отраженной и преломленной волнах соответственно имеем: 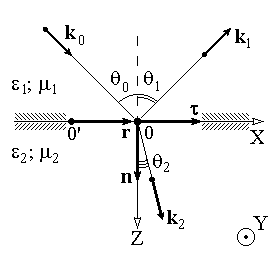 Рис. 1  (3) (3)где Законы отражения и преломления света на границе полностью определяются граничными условиями (1) и (2). Для электрического поля с учетом (3) граничные условия принимают вид: 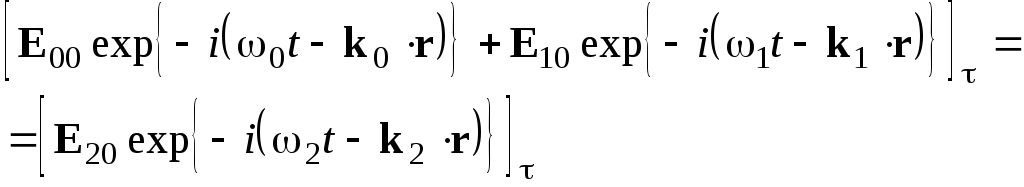 (4) (4)Отметим, что начало отсчета вектора r (точка 0’ ) совершенно произвольно. Если 0’ лежит не на поверхности раздела, то При этом в (4): Равенство (4) будет соблюдаться для произвольных значений r и t только при Отсюда следует, что частота ЭМВ при отражении и преломлении не меняется Выберем точку 0’ так, чтобы вектор Плоскость, в которой лежат волновой вектор k0 и нормаль к поверхности раздела n в точке падения луча, называется плоскостью падения. Из рис.1 видно, что 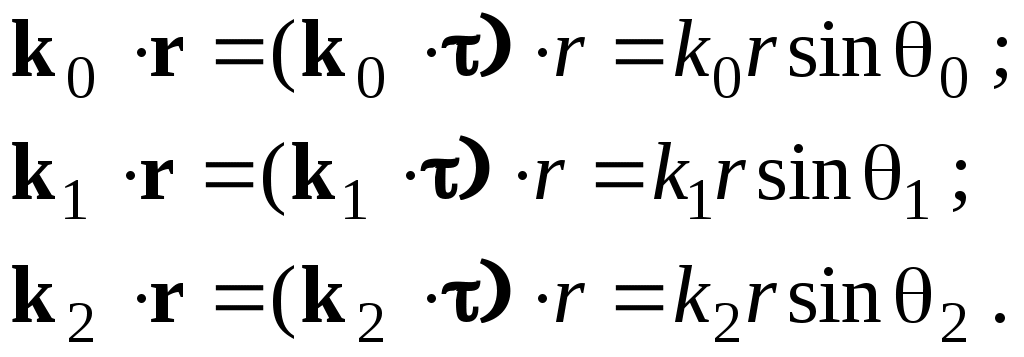 (9) (9)Тогда с учетом (7) получаем: или из (3) и (8): Вспомним, что Введем обозначение Тогда закон Снеллиуса примет вид: При 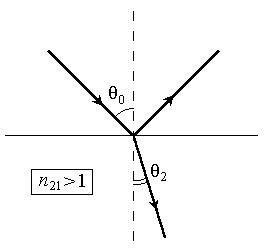 Рис. 2 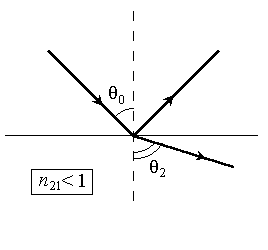 Рис. 3 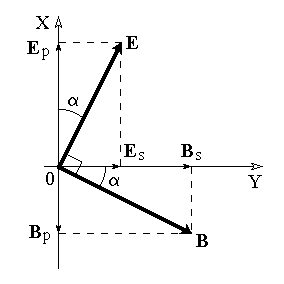 Рис. 4 Рис. 4Вообще говоря, вектор E0 в падающей волне может иметь произвольный азимут a (угол между E и плоскостью падения. Разложим векторы электромагнитного поля на две составляющие: перпендикулярные плоскости падения (будем обозначать их индексом s (или ^) и параллельные плоскости падения (будем обозначать их индексом p (или || )) (рис.4): 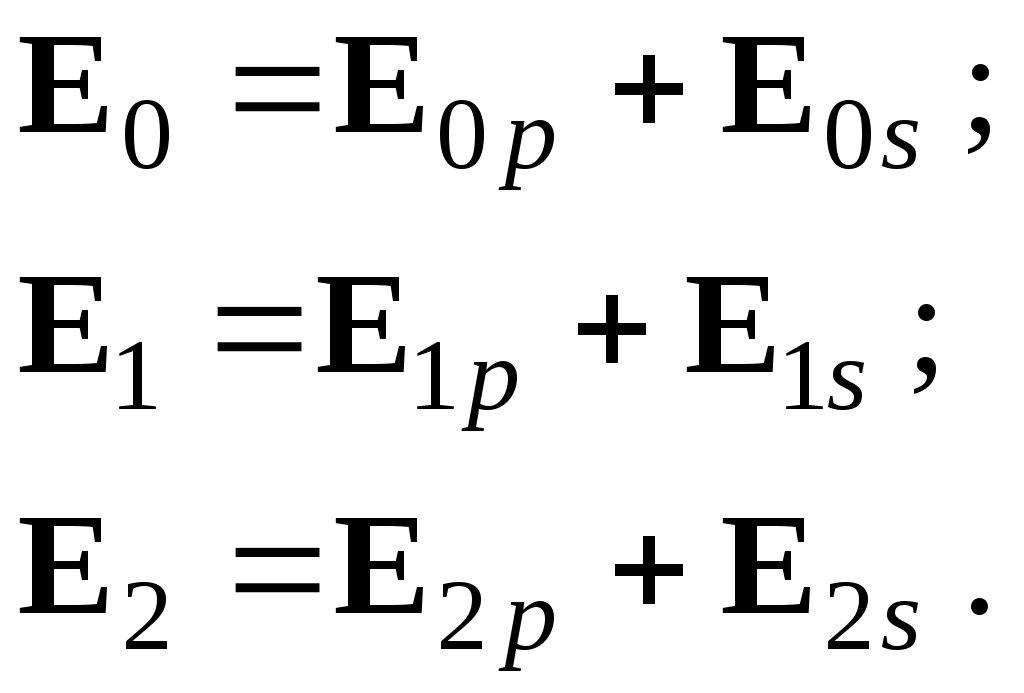 (16) (16)Видно, что векторы Т.о., плоскую волну с произвольным азимутом можно разложить на сумму волн, у одной из которых Ep (p – поляризация) лежит в плоскости падения, а у другой Es (s – поляризация) – перпендикулярна ей. Изучив поведение этих волн на границе с учетом принципа суперпозиции и аддитивности (в данном случае) плотностей потока энергии, получим поведение ЭМВ с произвольным азимутом. 1.2. Отражение и преломление s-поляризованной ЭМВ Введем единичные векторы в направлении волновых векторов:  Рис. 5 Рис. 5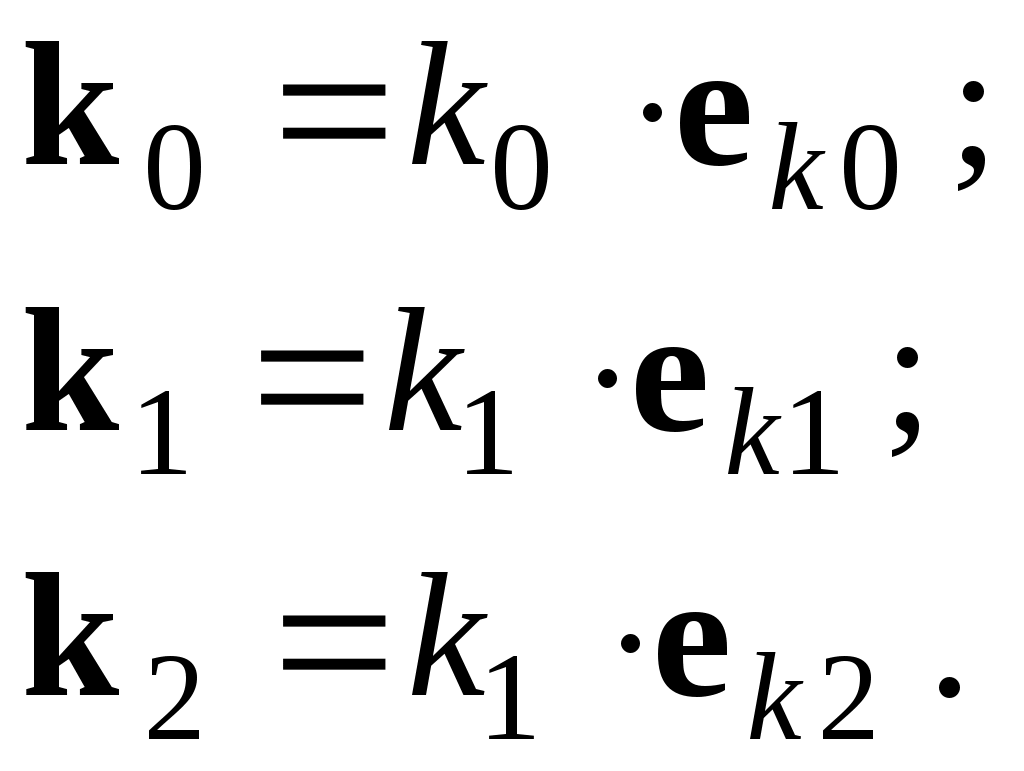 (17) (17)Как направлены векторы E1 и E2 заранее не известно. Направим условно их так, как показано на рис.5. Если знак получится отрицательный, значит векторы направлены в противоположную сторону. Граничные условия для s–поляризации (индексы s опустим): 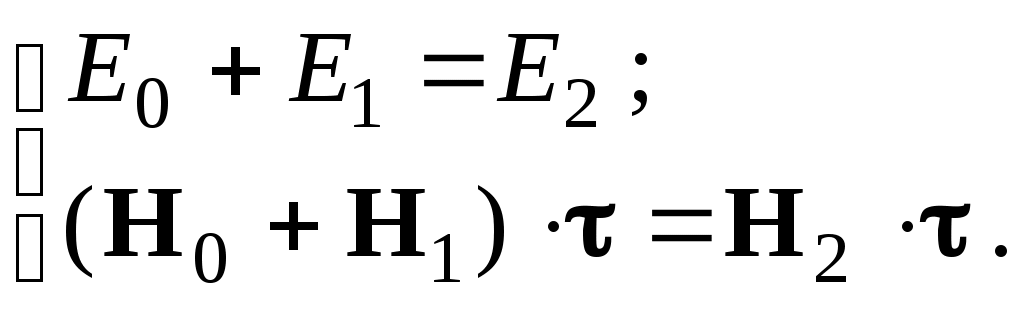 (18) – (19) (18) – (19)Обозначим Из рис.5 можно найти связь Для дальнейшего использования в (19) получим из (20) и (21) скалярное произведение для любой из рассматриваемых волн: С учетом известной из векторного анализа формулы получаем: Тогда из (19) имеем: Соотношения (25) и (18) совместно можно записать в виде: 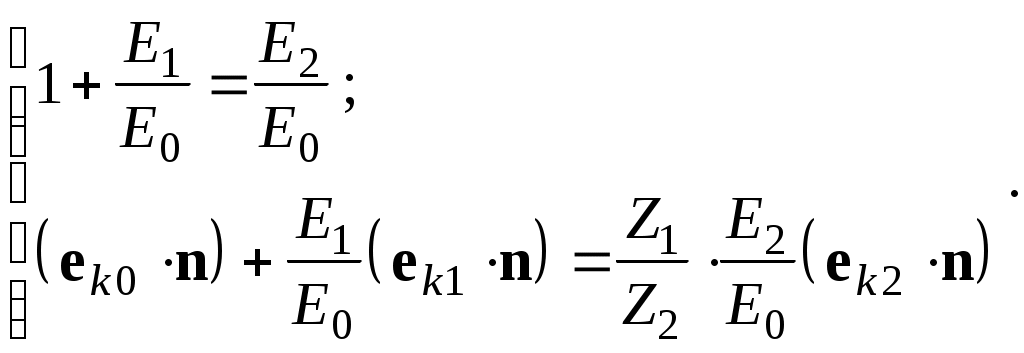 (26) (26)Обозначим: Учтем, что 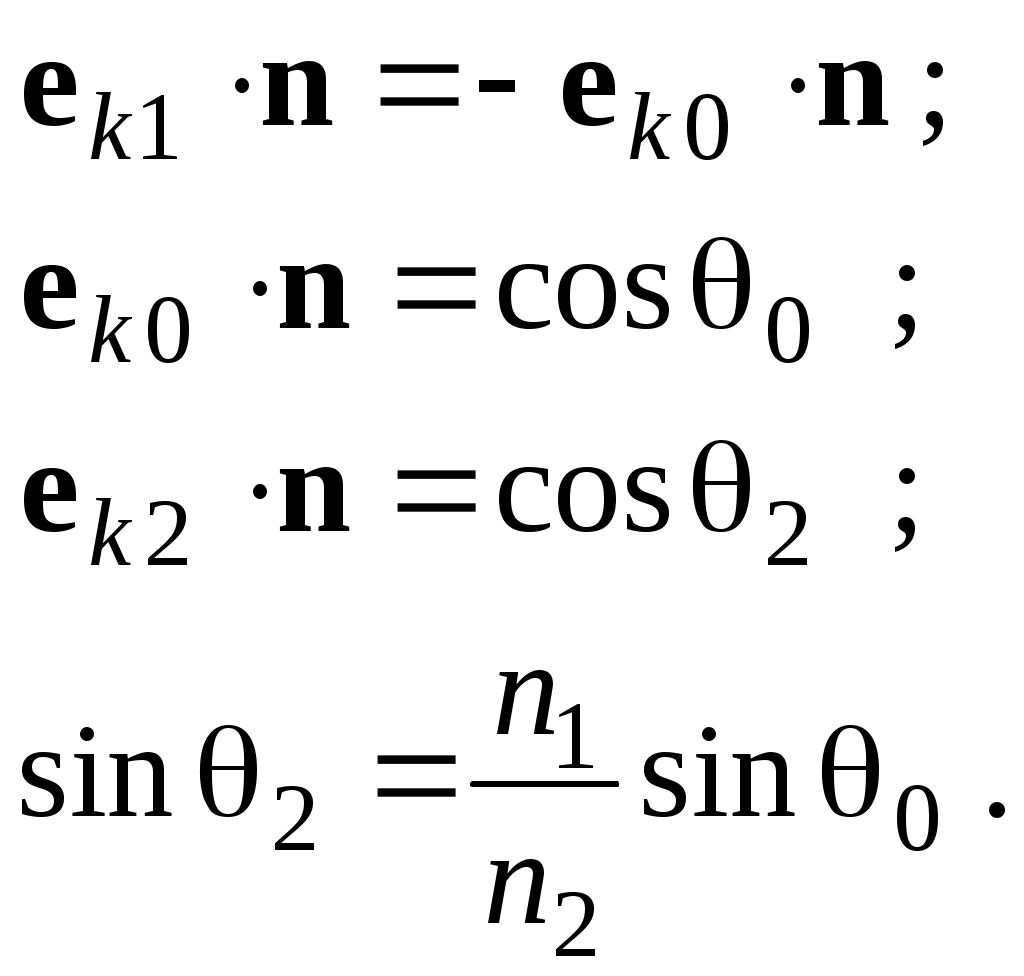 (29) (29)При 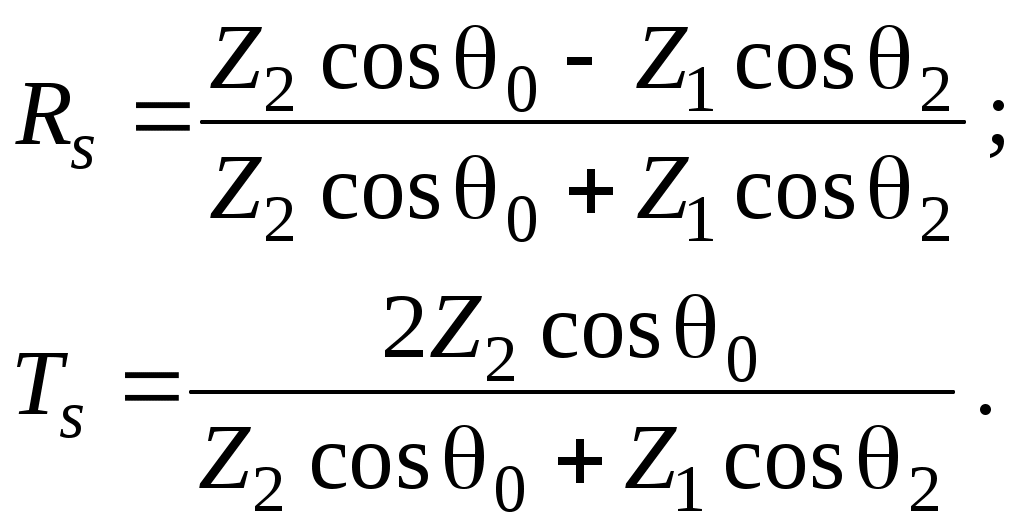 (30) – (31) (30) – (31)Для диэлектриков в оптическом диапазоне обычно 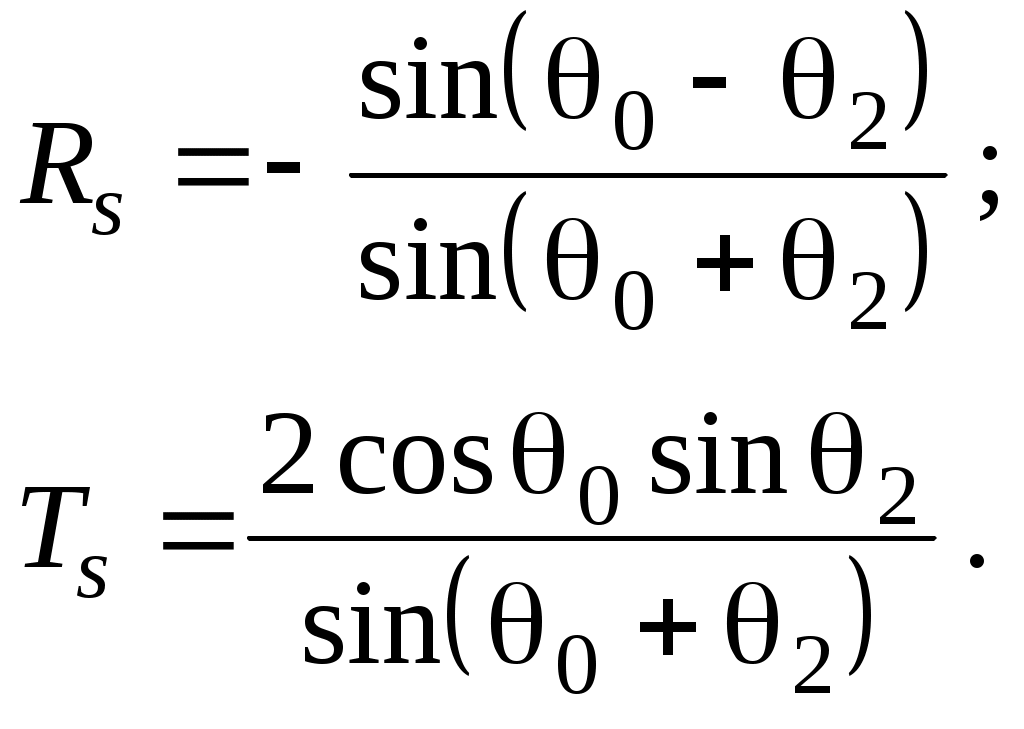 (32) – (33) (32) – (33)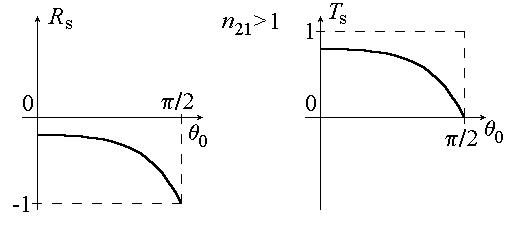 Рис. 6 Рис. 6Графики зависимостей При отражении света от диэлектрика с При отражении света от диэлектрика с 1.3. Отражение и преломление p–поляризованной ЭМВ 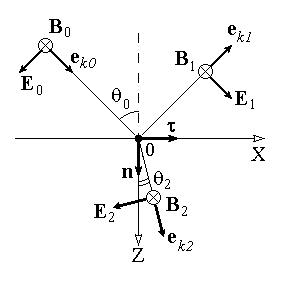 Рис. 7 Рис. 7Рассмотрение в данном случае проводится аналогично случаю s–поляризации. Для этого учтем, что 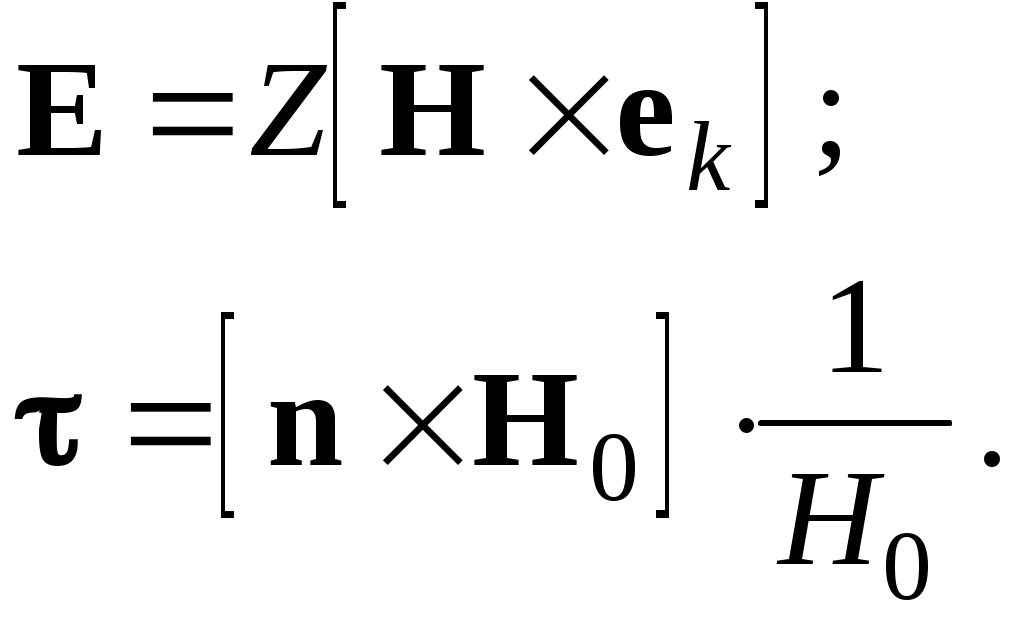 (34) – (35) (34) – (35)Отсюда Граничные условия для p–поляризации принимают вид: Подставляя (36) в (37), получаем: Для действительных углов преломления получаем обобщенные формулы Френеля для p–поляризации:  (41) – (42) (41) – (42)или для диэлектриков с m1 = m2 : 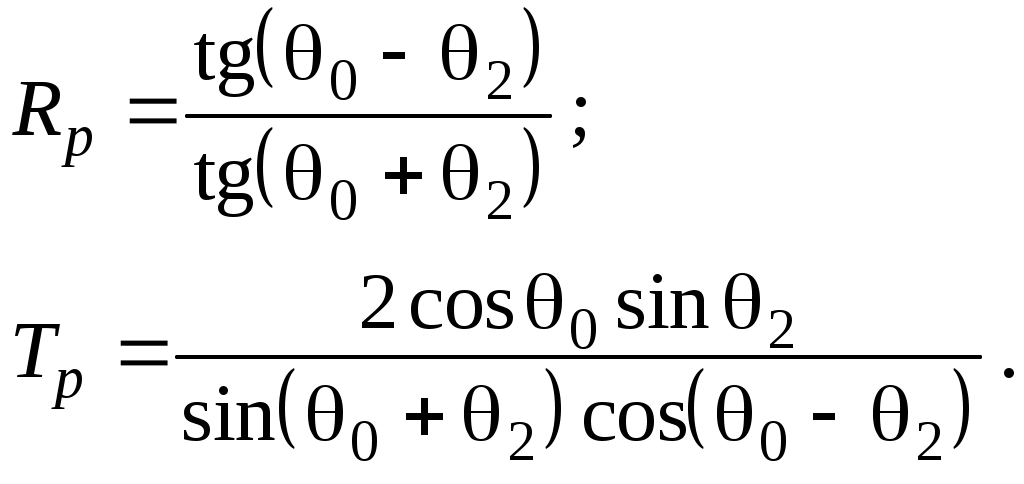 (43) – (44) (43) – (44)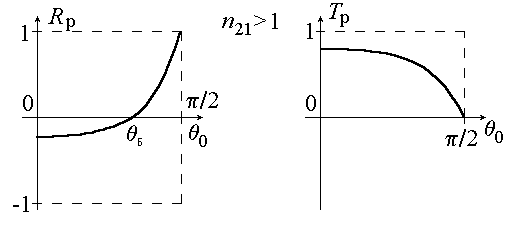 Рис. 8 Графики зависимостей 1.4. Явление Брюстера Из формулы (43) и из графика рис.8 видно, что для p–поляризованной волны при некотором угле падения 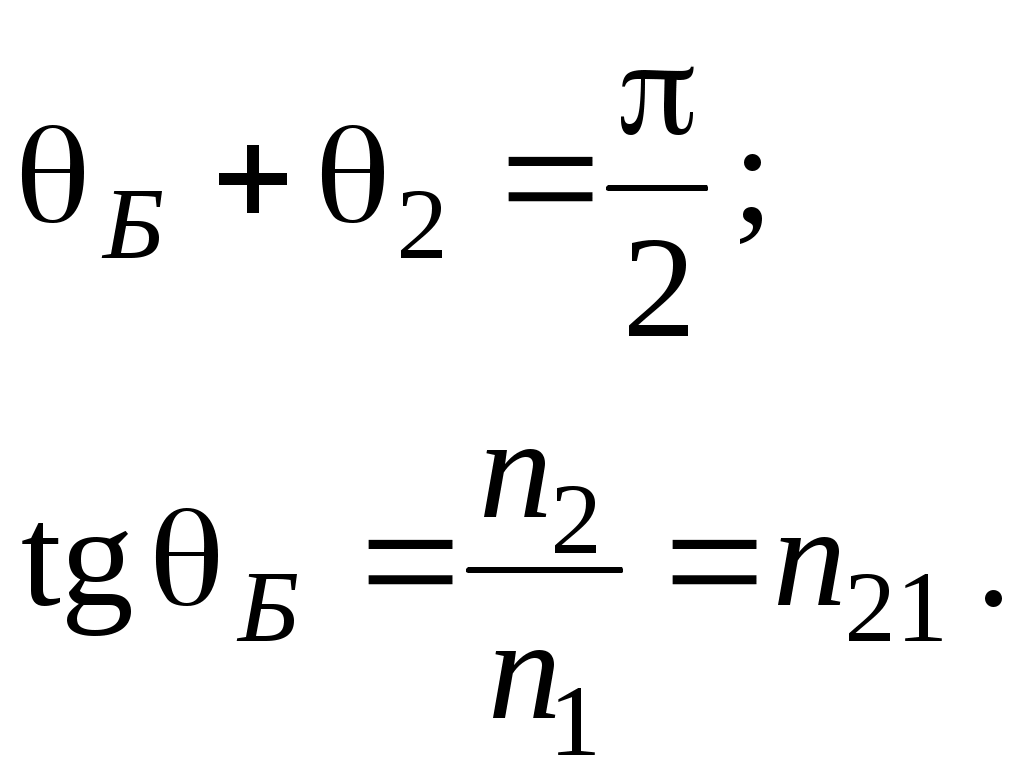 (45) (45)При переходе через угол Брюстера фаза колебаний отраженной волны скачком меняется на p. Заметим, что явлении Брюстера наблюдается тогда, когда направления преломленной и отраженной волны ортогональны. С физической точки зрения это можно объяснить следующим образом. Если связывать наличие отраженной волны с вынужденными колебаниями электронов во второй среде, то в направлении, перпендикулярном преломленной волне, не должна распространяться энергия, т.к. образующийся при этом диполь не излучает в направлении собственных колебаний. При При нормальном падении света ( 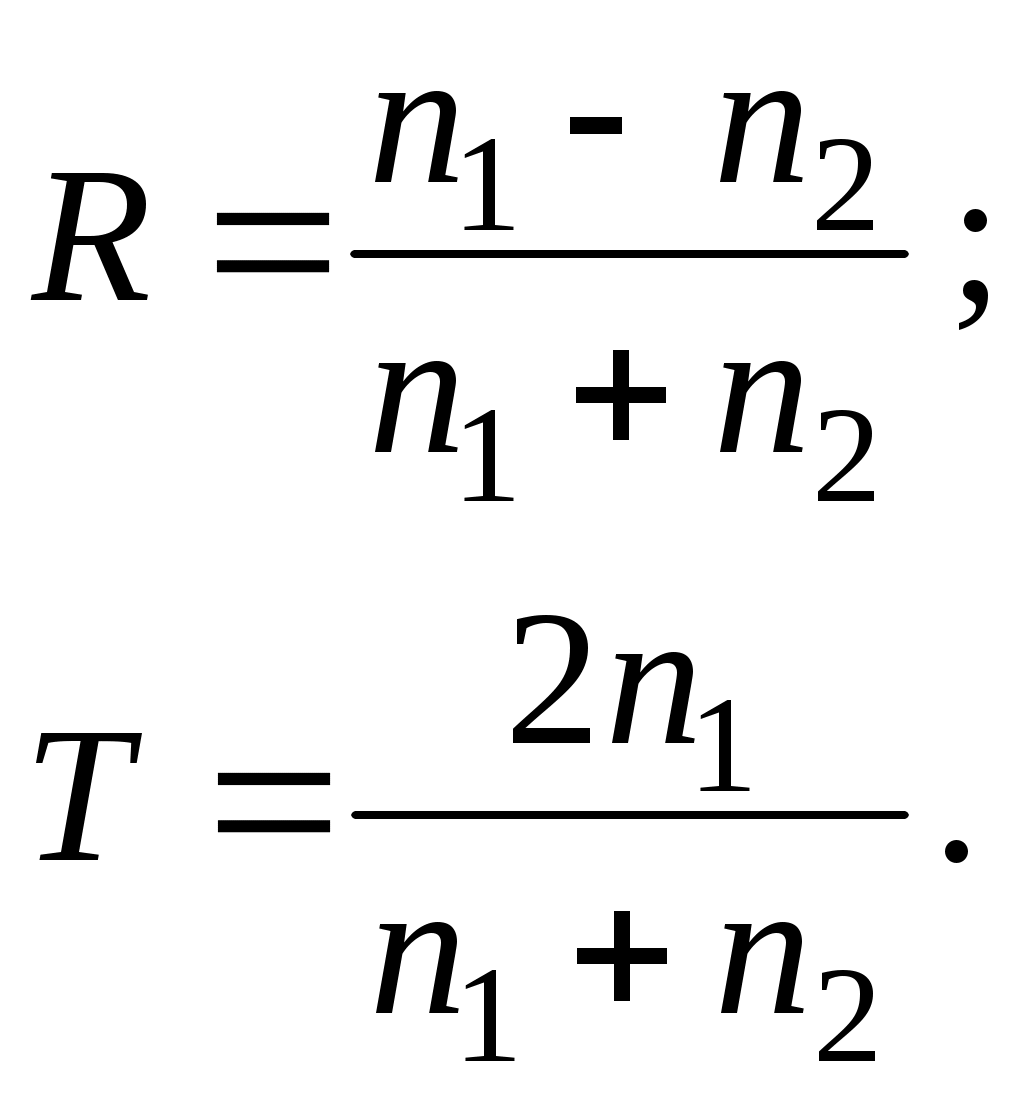 (46) – (47) (46) – (47)1.5. Энергетические соотношения при отражении и преломлении света Энергетическим коэффициентом отражения Энергетический коэффициент пропускания Т.к. , то для Â имеем: или с учетом (30), (31), (41), (42): 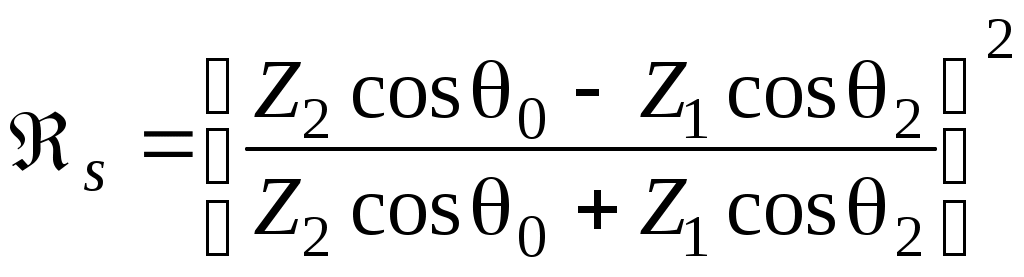 ; (54) ; (54)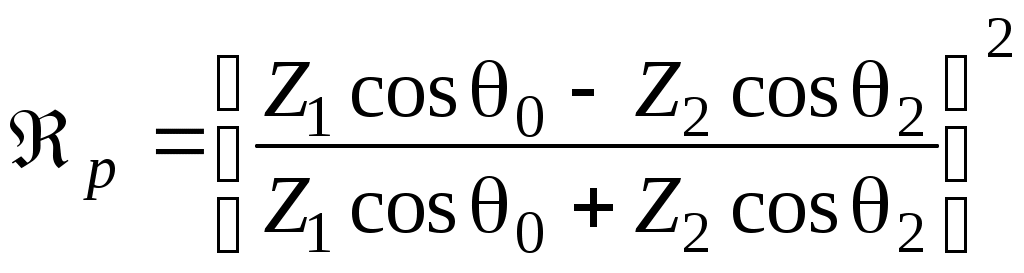 ; (55) ; (55)При q0 = 0 для m1 = m2 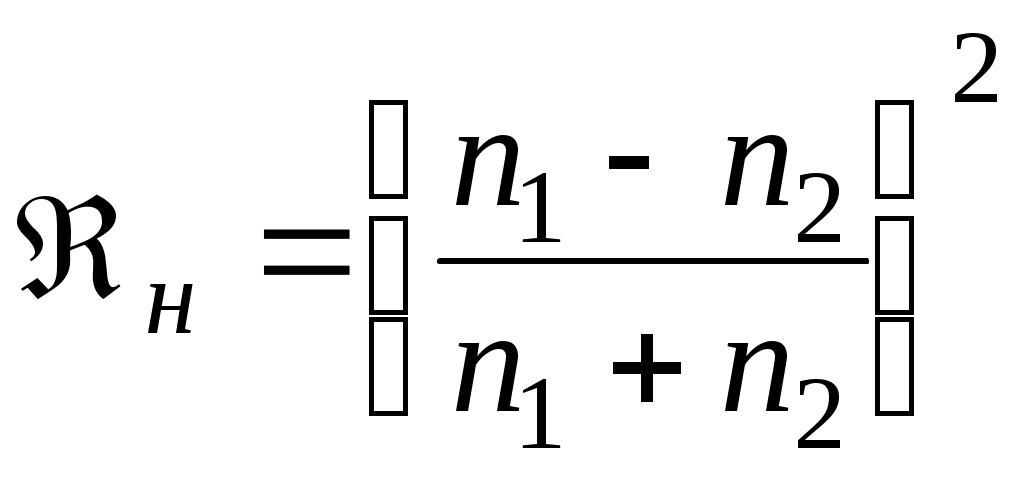 ; (58) ; (58)Прямой проверкой можно показать, что  Рис. 9 Рис. 9Это выражает закон сохранения энергии при отражении и преломлении света на границе раздела двух сред. Графики для 2. Описание установки Лабораторная установка (рис. 10) состоит из маломощного непрерывного лазера ((1) - излучатель, (2) – источник питания лазера), стеклянной плоскопараллельной пластины (3) с показателем преломления n=1.5, укрепленной на лимбе, имеющем градусную меру, фотоприемника (4) с цифровым индикатором и блоком питания (5). Показания цифрового индикатора фотоприемника (фототок) пропорциональны интенсивности света, падающего на фотоприемник. Излучение лазера линейно поляризовано. Все оптические элементы размещены на оптической скамье (6). 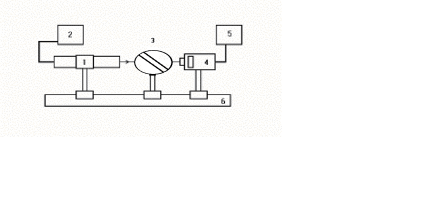 Рис.10. Схема лабораторной установки 3. Порядок выполнения работы 3.1. Установить оптические элементы, входящие в состав установки, на скамью. Проверить с помощью преподавателя правильное соединение элементов электрической части установки. ВНИМАНИЕ! В установке используется высокое напряжение и лазерное излучение. Приборы включают только инженер или преподаватель! 3.2. После включения приборов убрать стойку с пластиной, съюстировать оптические элементы так, чтобы луч, пройдя все элементы, попадал на фотоприемник (по максимуму фототока). Измерить фототок, соответствующий интенсивности падающей на пластину световой волны. Установить стойку с пластиной на место. Повторить юстировку. 3.3. Перекрыв лазерное излучение возле самого лазера, измерить темновой ток. В дальнейшем из показаний фотоприемника необходимо вычитать это значение. 3.4. Выставить плоскость поляризации излучения лазера перпендикулярно плоскости падения на стеклянную пластину. При необходимости повторить юстировку. 3.5. Снять зависимость фототока от угла падения света на пластину в диапазоне углов от 0 до 80 градусов с шагом 5 градусов. Угол падения устанавливается поворотом лимба. При изменении угла падения на каждом шаге необходимо подъюстировать фотоэлемент (по максимуму фототока). Измерения повторить не менее трёх раз. 3.6. Установить плоскость поляризации излучения параллельно плоскости падения. Повторить пункт 3.5. 3.7. Построить теоретические зависимости энергетических коэффициентов пропускания от угла падения для плоскопараллельной стеклянной пластины по формулам ((54)–(57)) с учетом отражения от двух граней пластины. На этих же графиках построить соответствующие экспериментальные зависимости с учетом статистической обработки результатов с доверительной вероятностью 90%. 3.8. Оценить по экспериментальным зависимостям угол Брюстера и сравнить с рассчитанным значением. 4. Контрольные вопросы и задания Сформулируйте граничные условия для векторов напряжённости электрического и магнитного полей волны. Какие физические факторы определяют значение угла Брюстера? Почему экспериментальная проверка формул Френеля может быть выполнена наиболее эффективно при углах Брюстера? Естественный свет падает на поверхность стекла (n=1.5) под углом Брюстера. Определить степень поляризации преломлённого луча. Найти степень поляризации узкого пучка лучей естественного света при прохождении плоскопараллельной пластины из стекла (n=1.5) если пучок падает на пластину под углом Брюстера. Найти азимуты колебаний в отражённых и преломлённой волнах, если азимут колебаний в падающей волне α0, а угол падения –Θ0. На поверхность стекла (n=1.5) под углом 450 падает линейно поляризованная волна. Найти коэффициенты отражения и пропускания, если: а) вектор напряжённости электрического поля перпендикулярен плоскости падения; б) колеблется в плоскости падения. Найти область углов падения линейно поляризованной волны из воздуха на поверхность воды (n=1.33), при которой коэффициент отражения больше 0.5. Рассмотреть случаи, когда плоскость поляризации падающей волны совпадает с плоскостью падения, перпендикулярна ей, падающий свет естественный. Из воды (n=1.33) на границу раздела с воздухом под углом 600 падает световая волна. Найти критический угол и сдвиги фаз колебаний напряжённости электрического поля φ┴ и φ║. Лабораторная работа ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ СТЕКЛА ЦЕЛЬ РАБОТЫ: изучение одного из наиболее простых методов определения показателя преломления прозрачного вещества; ознакомление с работой микроскопа. ПРИНАДЛЕЖНОСТИ: микроскоп, штангенциркуль, набор прозрачных плоскопараллельных пластинок. 1. Вывод основного соотношения В основу метода измерения показателя преломления в данной работе положена зависимость параметров оптического изображения данного предмета от показателя преломления окружающей среды. Связь размеров предмета и изображения находится с помощью закона Снеллиуса, вывод которого из граничных условий приведён в предыдущей работе (соотношение 13) . Р 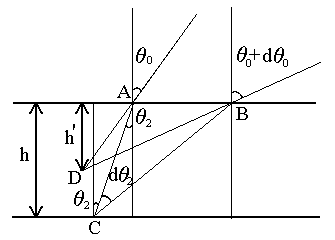 ассмотрим следующую задачу. На внутренней стороне стеклянной пластинки в точке С находится предмет. Толщина пластинки h, показатель преломления n. Пусть предмет С наблюдается глазом (см. рис.1). Рис.1 Нас интересует вопрос: на каком расстоянии h' от верхней поверхности пластинки получается изображение точки С?Для решения этого вопроса предположим, что из точки С выходят два луча, угол Имеем, откуда Поэтому 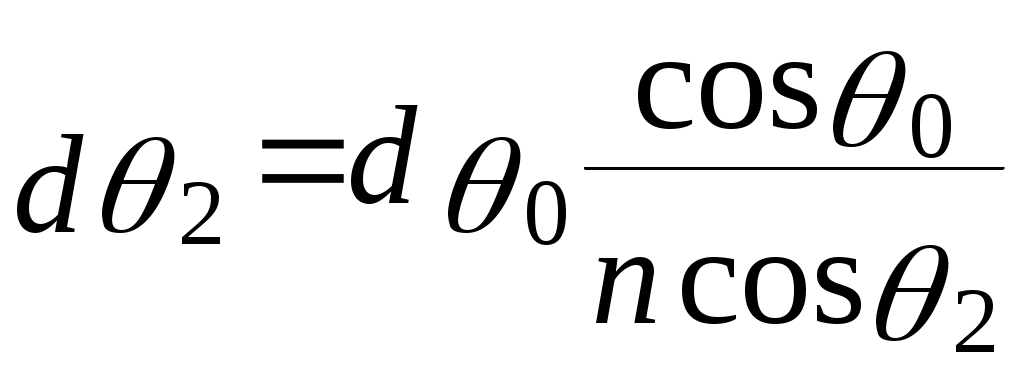 Для нахождения h` заметим, что АВ = h 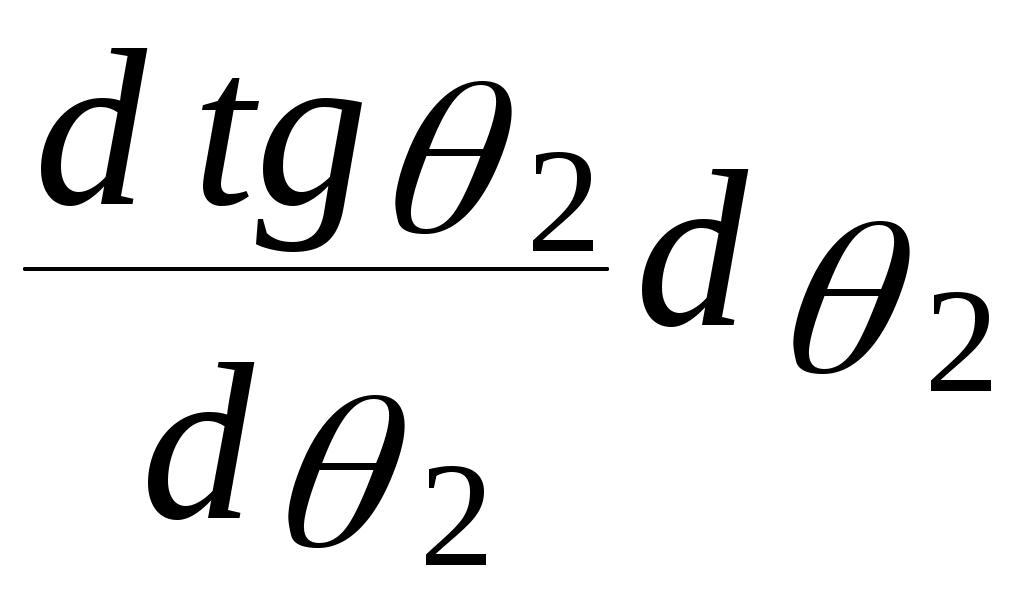 (1) (1)С другой стороны АВ= h` 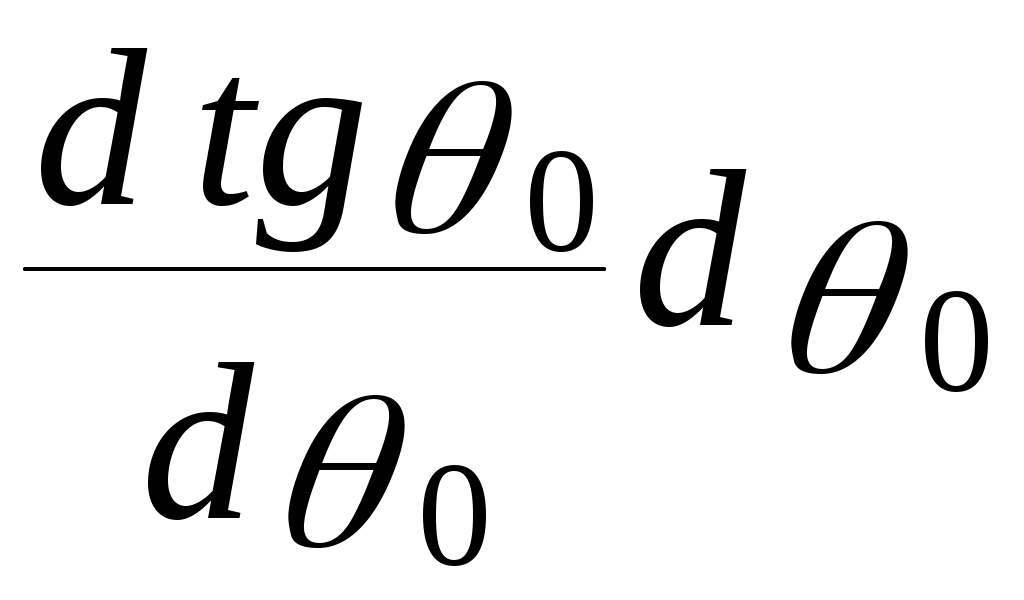 (2) (2)Поэтому сравнивая (1) и (2), получим: h` =  h = h = 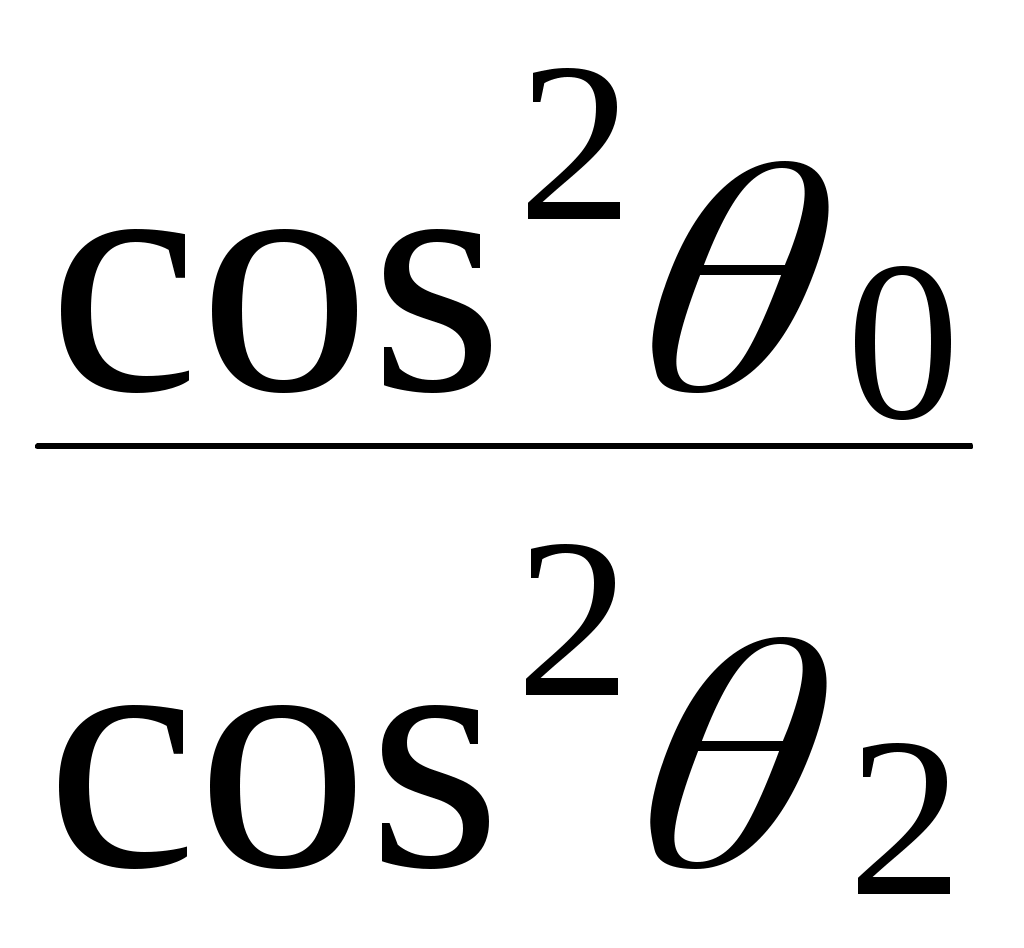 h h 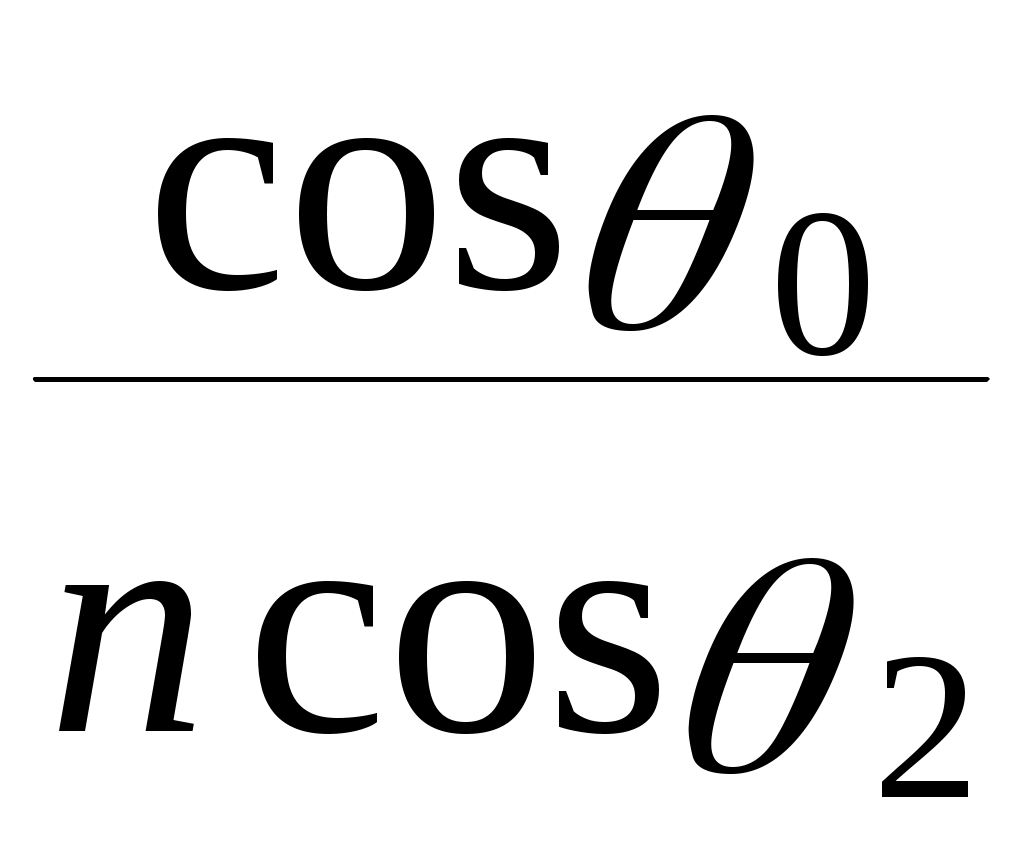 = h = h 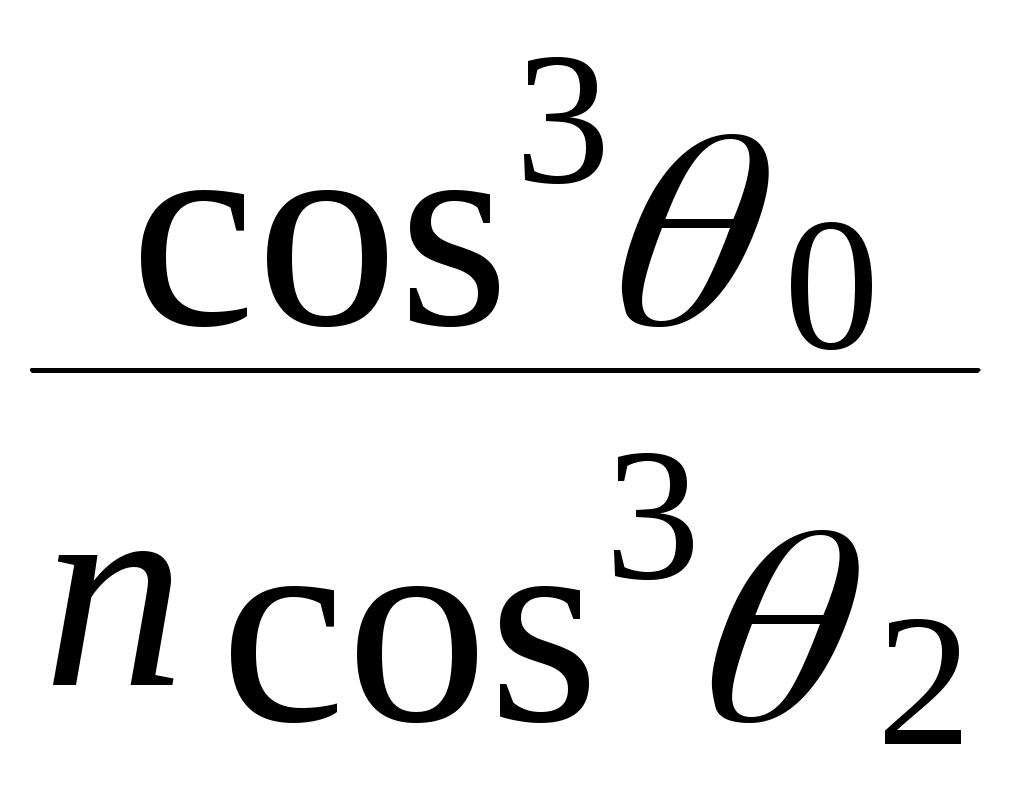 (3) (3)Выражая h` = h 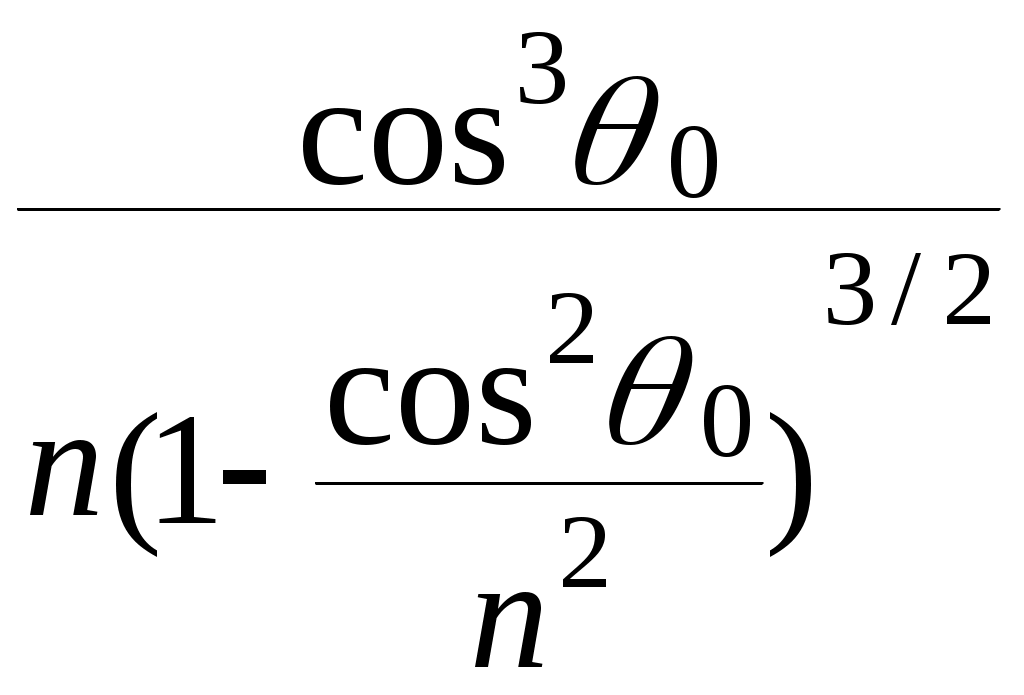 . (4) . (4)Для частного случая 2. Описание установки В 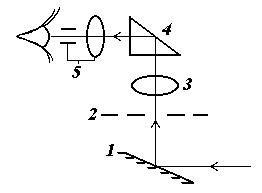 работе для определения показателя преломления стекла используется микроскоп. Оптическая схема прибора показана на рис.2. Осветительная часть состоит из зеркала (1), а наблюдательная включает в себя предметный столик (2), куда помещается исследуемый объект, объектив (3), призму (4) и окуляр (5). Рис.2. Оптическая схема микроскопа Порядок выполнения работы. . Для измерений используются две плоскопараллельные пластинки (стекло и оргстекло) с разными толщинами. 3.1. С помощью штангенциркуля измерить их толщины 3.2. Определить средние значения истинных толщин пластинок 3.3. Поместить пластинку на предметный столик. Поднять тубус микроскопа с помощью микрометрического диска, вращая его против часовой стрелки до упора. С помощью ручек грубой фокусировки получить четкое изображение верхнего следа. 3.4. Вращая диск микрометрической фокусировки против часовой стрелки, получить четкое изображение нижнего следа. 3.5. Определить видимую толщину пластинки 3.6. Повторить пп.3.3. – 3.5. пять раз для обеих пластинок. 3.7. Определить средние значения видимых толщин пластинок 3.8. По формуле 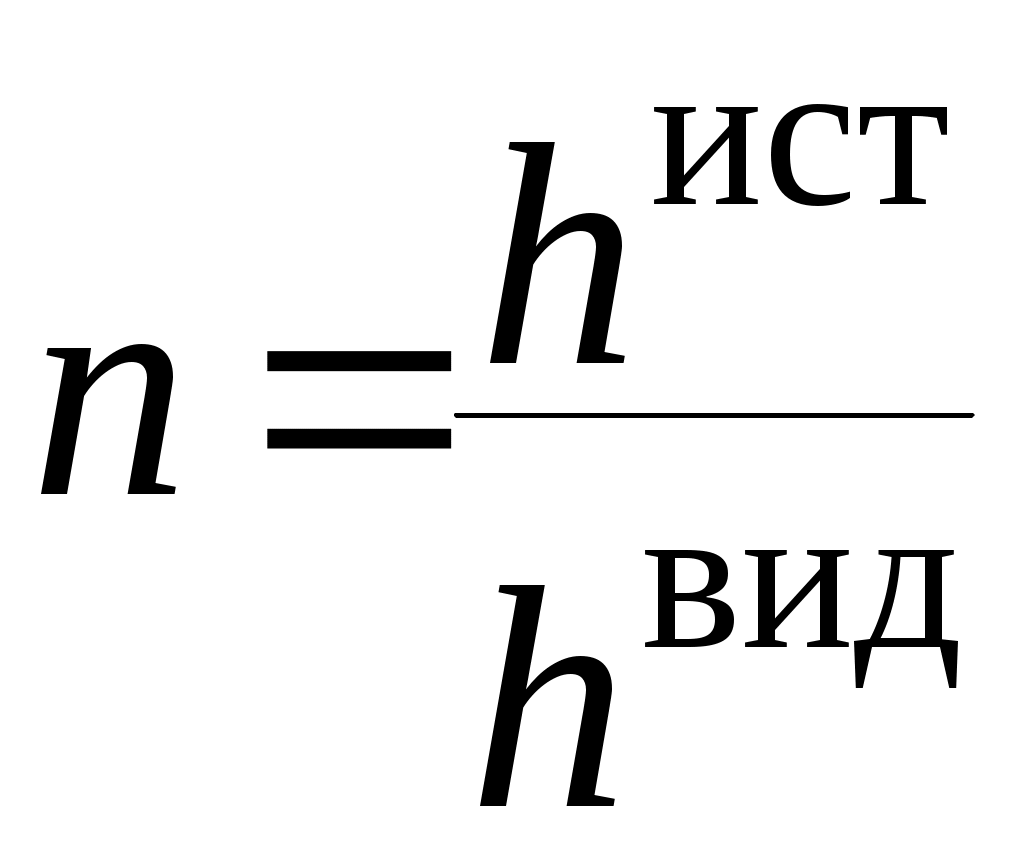 найти коэффициент преломления стекла. найти коэффициент преломления стекла.3.9. Вычислить доверительный интервал значений 3.10. Занести результаты в таблицу 1. Таблица 1. Истинные и видимые толщины пластинок
4. Контрольные вопросы и задания 1. Для какой формы границы раздела двух сред справедлив закон Снеллиуса для плоской волны? 2. Можно ли пользоваться законом преломления Снеллиуса для световой волны, падающей из воздуха на границу диэлектрического шара с показателем преломления n = 1.5 и радиусом R = 10 см. 3. На дне сосуда, наполненного водой до высоты h, находится точечный источник света. На поверхности воды плавает круглый диск так, что его центр находится над источником. При каком минимальном радиусе диска лучи от источника не будут выходить из воды? 4  . На шар радиуса R, изготовленный из материала с меньшим показателем преломления, чем показатель преломления среды, где находится шар, падает пучок параллельных лучей. Определить радиус светового пучка, который может проникнуть в шар. 5. Стеклянная пластинка, показатель преломления которой n, находится в воздухе. Могут ли лучи, падающие на грань 1, после преломления на ней испытать полное внутреннее отражение на грани 2? 6. То же, что и в п.5, но в случае, когда грань и пластинки граничит с жидкостью с показателем преломления n3>1. 7. То же, что и в п.5, только вместо жидкости помещается плазма с показателем преломления n3<1. 8. Что такое мнимое изображение? Когда оно получается и трактуется? 9. К зеркалу подносится фотопластинка. Будет ли на фотопластинке запечатлено изображение предмета, находящегося перед зеркалом? 10. Как объясняется явление миража? 11. Объяснить причину искривления солнечных лучей в атмосфере Земли. К чему приводит такое искривление? (Рассмотреть восход и заход Солнца). 12. Какие еще методы (кроме описанного в данной работе) вы можете предложить для определения показателя преломления? 13. Доказать, что если световой луч проходит несколько сред разделенных плоскопараллельными границами, то направление выходящего луча зависит только от направления входящего луча и от показателей преломления первой и последней сред. 14. Под стеклянной пластинкой толщины d=15 см лежит маленькая крупинка. На каком расстоянии l от верхней поверхности пластинки образуется ее видимое изображение, если луч зрения перпендикулярен к поверхности пластинки, а показатель преломления стекла n = 1.5?  ВЗАИМОДЕЙСТВИЕ СВЕТА С ВЕЩЕСТВОМ Лабораторная работа ЗАКОН БУГЕРА ЦЕЛЬ РАБОТЫ: Ознакомиться с экспериментальным методом исследования оптических свойств поглощающих материалов. ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, набор плоскопараллельных пластин, фотоприемник, оптическая скамья. Теоретическая часть В диэлектриках скорость световых ЭМВ зависит от частоты. Это явление называется дисперсией. Дисперсия проявляется лишь в распространении немонохроматических волн, т.к. ее монохроматические составляющие с различными частотами распространяются с различными скоростями. Дисперсия является следствием зависимости поляризуемости атомов от частоты. Для нахождения явного вида (), входящей в материальные уравнения, воспользуемся микроскопической классической теорией взаимодействия электромагнитного поля волны с веществом. Микроскопическая теория исходит из некоторой идеализированной модели строения вещества. Наибольшей простотой отличается модель газообразной среды, т.к. для нее в первом приближении можно не учитывать взаимодействие атомов или молекул и считать, что действующее на отдельный атом поле совпадает со средним полем ЭМВ. В таких условиях для получения макроскопического материального уравнения достаточно рассмотреть действие поля ЭМВ на изолированный атом. Вообще говоря, применять классическую теорию к таким процессам нужно крайне осторожно. Но в данном случае квантовая теория дисперсии приводит к таким же результатам, что и классическая. 1.1. Классическая электронная теория дисперсии В классической теории дисперсии электрон, с которым взаимодействует электромагнитное поле (внешний, или оптический электрон), в атоме рассматривается как затухающий дипольный осциллятор, характеризуемый определенной собственной частотой о и постоянной затухания , так что уравнение его движения в поле E(t) = Eoe–it световой волны имеет вид: где r – смещение электрона из положения равновесия. Будем искать решение этого уравнения в виде: В результате получим: Дипольный момент атома p(t), индуцированный полем E(t): Если N – концентрация электронов с собственной частотой колебаний 0, то поляризация P среды определяется как С другой стороны поляризация среды равна где – линейная диэлектрическая восприимчивость среды, которая вообще говоря, зависит от частоты . Учтем также, что векторы D, E и P связаны соотношением: Тогда из (6) и (7) следует, что диэлектрическая проницаемость: а из (4), (5), (6) имеем: или Т.к. Тогда с учетом (10) имеем уравнения: 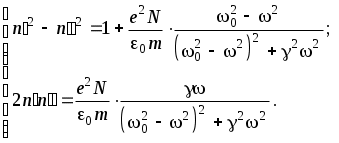 (12) (12)Для прозрачных или частично прозрачных в оптическом диапазоне диэлектриков очень мало. Тогда Из этого приближения получаем: 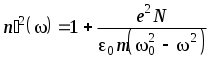 . (14) . (14)Если в среде дисперсию определяют различные ансамбли электронов с собственными частотами 0i и концентрацией Ni, то формулу (14) можно обобщить: 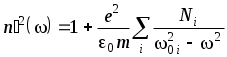 . (15) . (15)В этой формуле не учтены колебания ионов. Т.к. их масса много больше массы электронов, то собственные частоты ионов лежат в дальней инфракрасной области. Нормальная дисперсия. Вдали от собственных резонансов величина Тогда 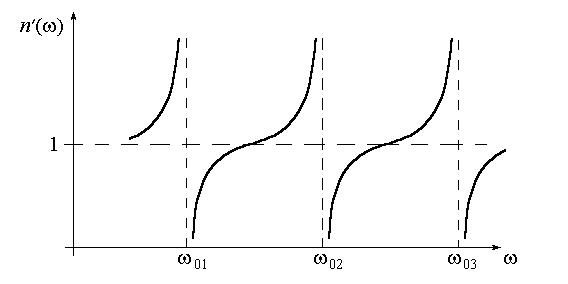 Рис. 1 Графическая зависимость Если действительная часть показателя преломления увеличивается с ростом частоты, то дисперсия называется нормальной. Нормальная дисперсия наблюдается во всей области прозрачности диэлектриков. Для малых частот ( << 0i) формула (17) дает статическое значение показателя преломления: Это значение может существенно отличаться от значения показателя преломления для оптических частот. (Например, для воды в области оптических частот n = 1,33 , а статическое значение Для больших частот ( >> 0i ) Т.о. для коротковолнового излучения диэлектрик является оптически менее плотной средой, чем вакуум. Например, для рентгеновского излучения может наблюдаться полное отражение. Кроме того, при очень больших частотах характер связи электронов роли не играет, а показатель преломления n зависит лишь от общей концентрации всех электронов. Аномальная дисперсия . Пренебрежение затуханием ( = 0) привело к тому, что 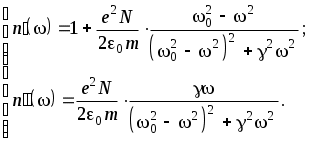 (20) (20)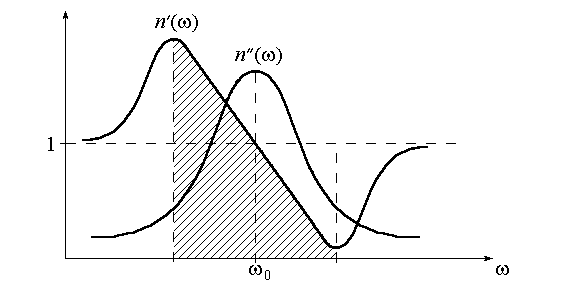 Рис.2 Дисперсионные кривые (20) представлены на рис.2. Вблизи резонансной частоты 0 показатель преломления |
