|
|
лабораторный практикум. Практикум волгоград 2014 Печатается по решению редакционноиздательского совета
ИНТЕРФЕРЕНЦИЯ СВЕТА
Лабораторная работа
ИНТЕРФЕРЕНЦИЯ СФЕРИЧЕСКИХ ВОЛН
(БИПРИЗМА ФРЕНЕЛЯ)
ЦЕЛЬ РАБОТЫ: изучение явления двухлучевой интерференции с помощью бипризмы Френеля, определение длины световой волны с использование данной интерферометрической схемы.
ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, две линзы (собирающая и рассеивающая), бипризма Френеля, экран, линейка, оптическая скамья с набором рейтеров.
1. Теоретическая часть [1¸6]
1.1. Интерференция волн
В эксперименте возможна ситуация, когда интенсивность света, создаваемая какими-либо двумя источниками, не равна сумме интенсивностей отдельных источников. Оказывается, что если свет от одного источника разделить прибором на два пучка и заставить их проходить разные пути, а затем наложить их друг на друга, то интенсивность их в области суперпозиции пучков будет изменяться от точки к точке. Она может достигать максимума, превышающего сумму интенсивностей пучков, и минимума, который может оказаться равным нулю. Это явление называется интерференцией. Оказывается, что при суперпозиции пучков строго монохроматического света интерференция возникает всегда. Однако, свет от физических источников никогда не бывает строго монохроматическим. Как следует из теории излучения атома, его амплитуда и фаза флуктуируют непрерывно и так быстро, что ни глаз, ни быстрый физический детектор не могут уследить за их изменениями.
Если две световых волны происходят от одного источника, то возникающие в них флуктуации амплитуды и фазы, вообще говоря, коррелированы, и о таких волнах говорят, что они полностью или частично когерентны, в зависимости от того, будет ли эта корреляция полной или частичной. В общем случае колебания (или волны) называются когерентными, если разность их фаз остается постоянной (или изменяется по определенному закону) во времени. В световых пучках от разных источников флуктуации совершенно независимы и пучки, как говорят, взаимно некогерентны. При наложении таких пучков от независимых источников интерференция в обычных экспериментальных условиях не наблюдается. Детальный анализ показывает, что «степень корреляции» между флуктуациями в двух световых пучках определяет «четкость» интерференционных эффектов, возникающих при суперпозиции пучков и, наоборот, «степень корреляции» сама определяется этими эффектами.
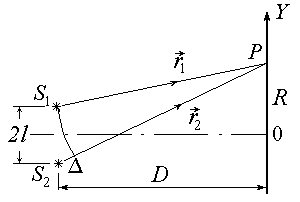
Рис.1
Рассмотрим вначале классическую схему Юнга наблюдения интерференционной картины для простейшего случая двух гармонических волн. Пусть два точечных источника S1 и S2 , расположенных на расстоянии 2l друг от друга излучают две монохроматические сферические когерентные волны 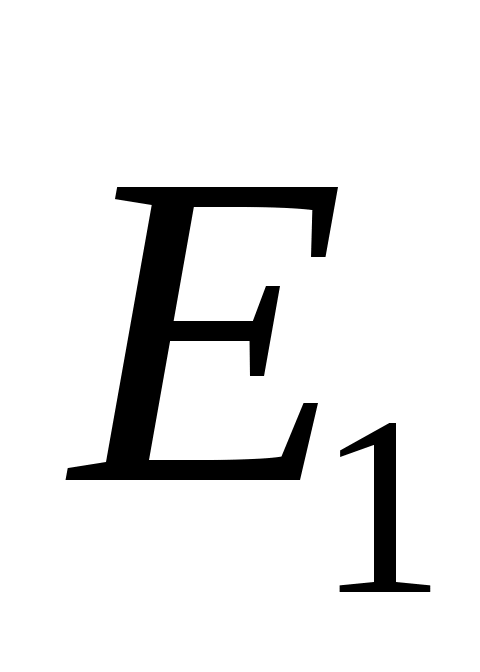 и и 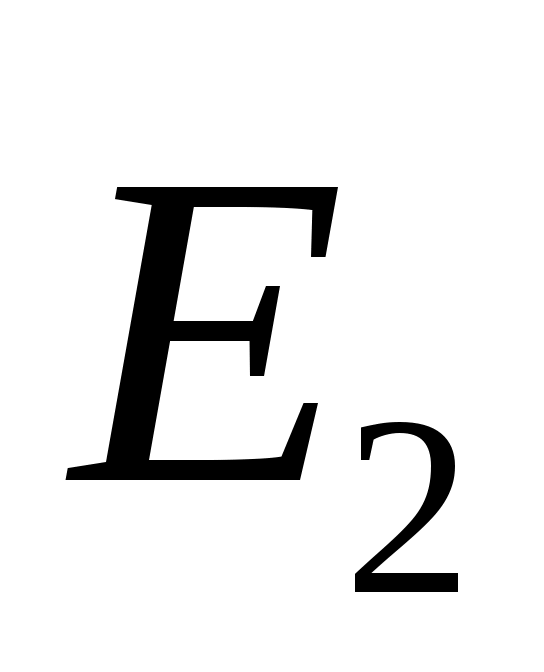 (рис.1). Предположим, что расстояние D от источников до экрана значительно больше 2l и положим для простоты, что амплитуды волн E1и E2в точке Р одинаковы и равны Е0 . Найдем результирующую амплитуду волн в точке Р, если (рис.1). Предположим, что расстояние D от источников до экрана значительно больше 2l и положим для простоты, что амплитуды волн E1и E2в точке Р одинаковы и равны Е0 . Найдем результирующую амплитуду волн в точке Р, если
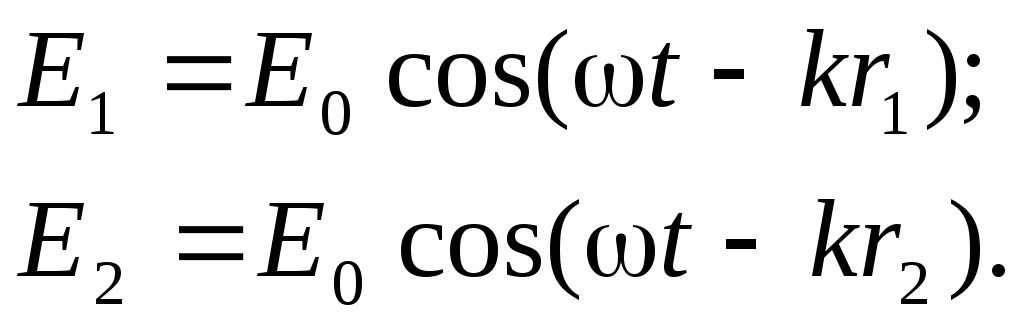 (1) (1)
Тогда суммарная волна в точке Р:
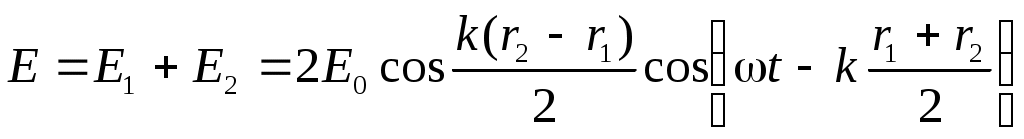 . (2) . (2)
Введем величину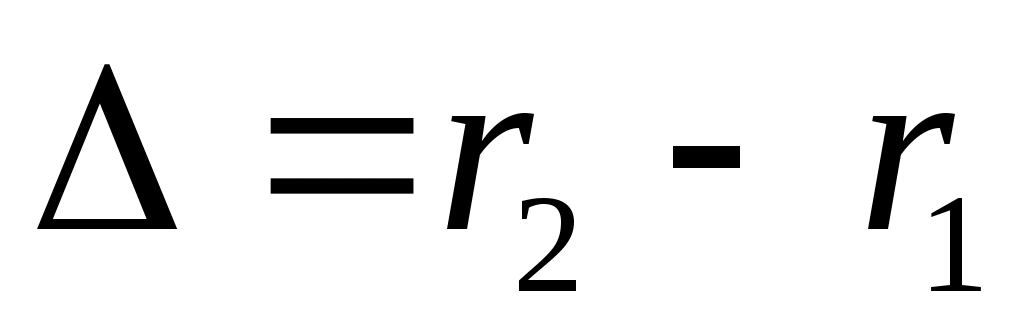 , называемую геометрической разностьюхода. Тогда интенсивность света будет равна: , называемую геометрической разностьюхода. Тогда интенсивность света будет равна:
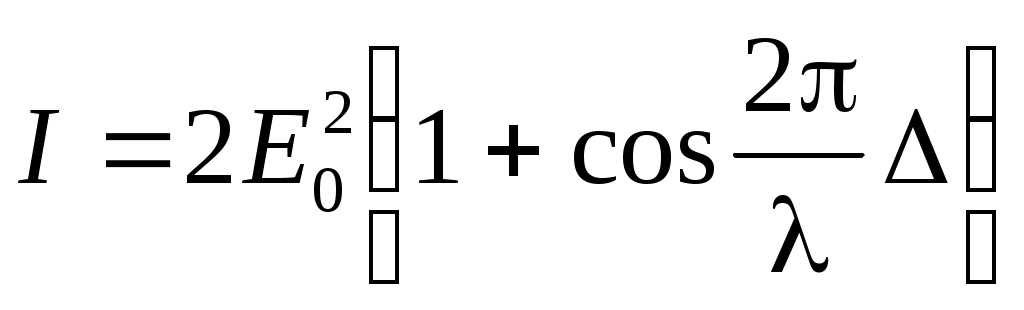 . (3) . (3)
Видим, что
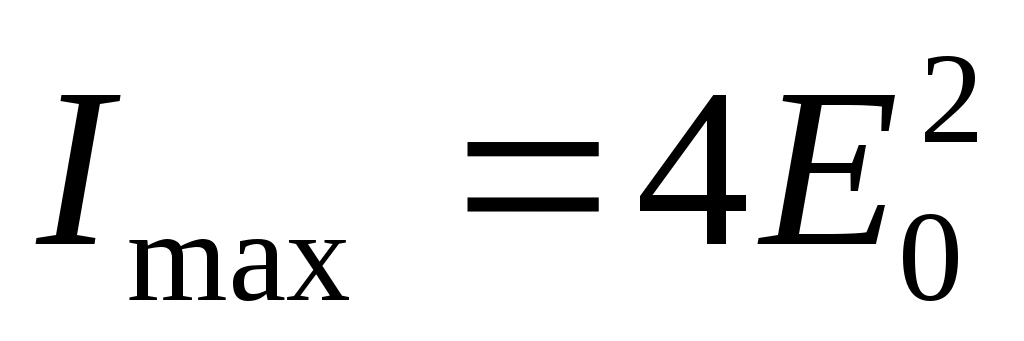 при при 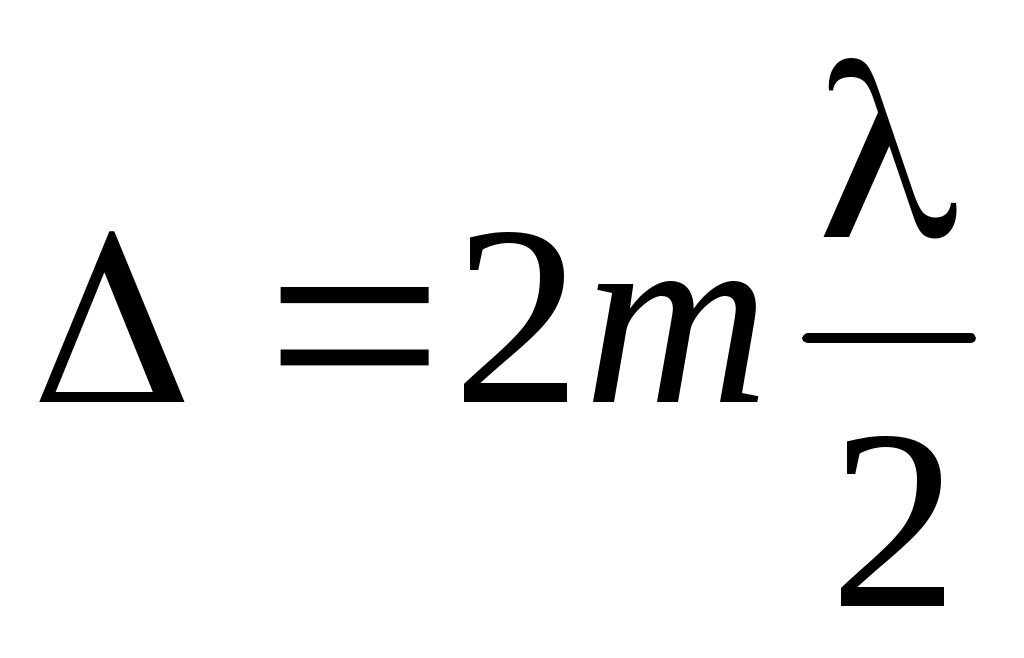 ; (4) ; (4)
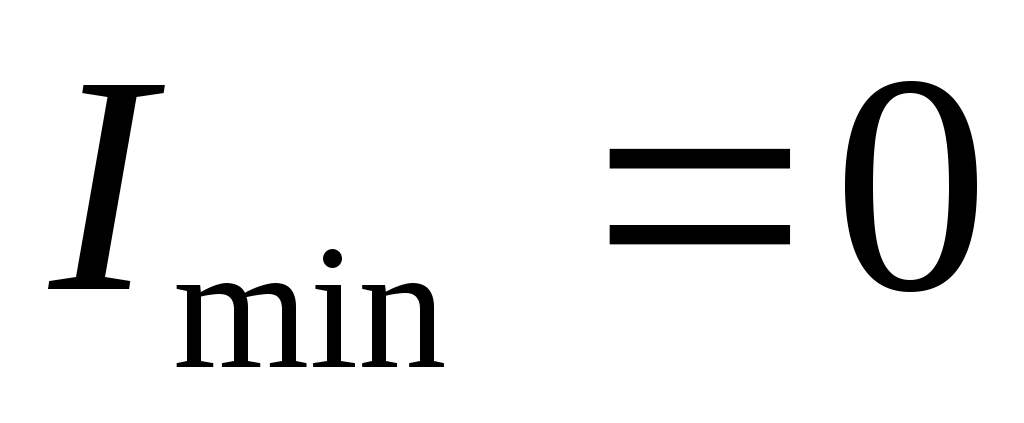 при при  . (5) . (5)
Таким образом, в результате наложения двух когерентных волн мы будем наблюдать в пространстве (или на экране, как это делается в эксперименте) чередующуюся в зависимости от разности хода картину максимумов и минимумов, называемую интерференционными полосами.
1.2. Получение когерентных световых волн с помощью бипризмы Френеля
Для получения когерентных световых волн от реальных источников пользуются следующим искусственным приемом. Волновой фронт разделяют на несколько частей. Полученные таким образом волны проходят различные оптические пути и при дальнейшем сложении уже обладают разностью хода, оставаясь когерентными. Потому, что разность хода зависит только от конструкции прибора.
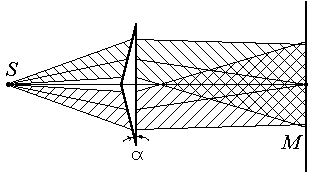
Рис.2
На рис. 2 приведен способ деления фронта волны на две части с помощью бипризмы Френеля. Важно отметить, что в практических приборах разность хода не делается обычно больше 100 ¸ 200 мм, т.к. длительность излучения атома
10-8 с, и при большой разности хода может случиться, что будут складываться волны, полученные уже от разных актов испускания, т.е. когерентность нарушится. Бипризма Френеля имеет малые преломляющие углы (a = 30/ ) и разность хода, приобретаемая волнами здесь мала. После преломления в бипризме падающий пучок света разделяется на два когерентных пучка с источниками в мнимых изображениях S‘ и S“ источника S (рис.3). Вычислим разность хода волн, приходящих в точку Р, через геометрические размеры оптической схемы.
 . (6) . (6)
Считая, что в практических схемах d » D, ОР = y«D и следовательно: 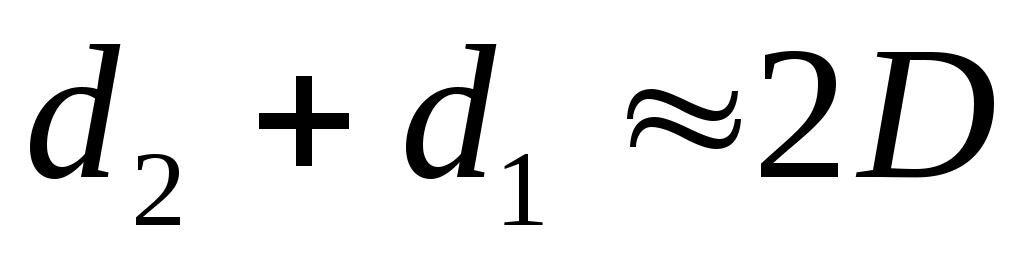 , получим: , получим:

Рис.3
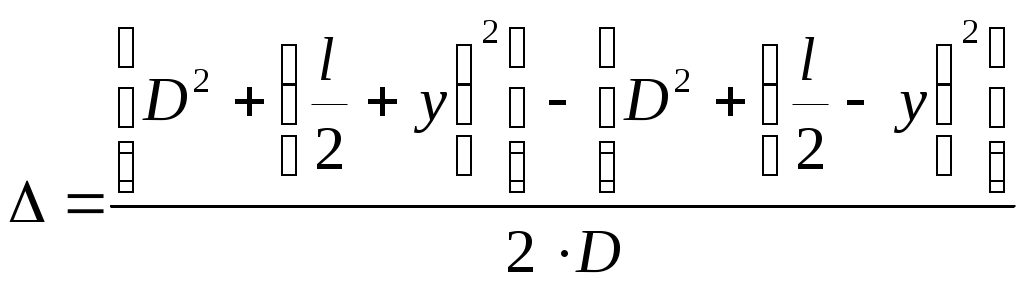 (7) (7)
Преобразуя (7), получим:
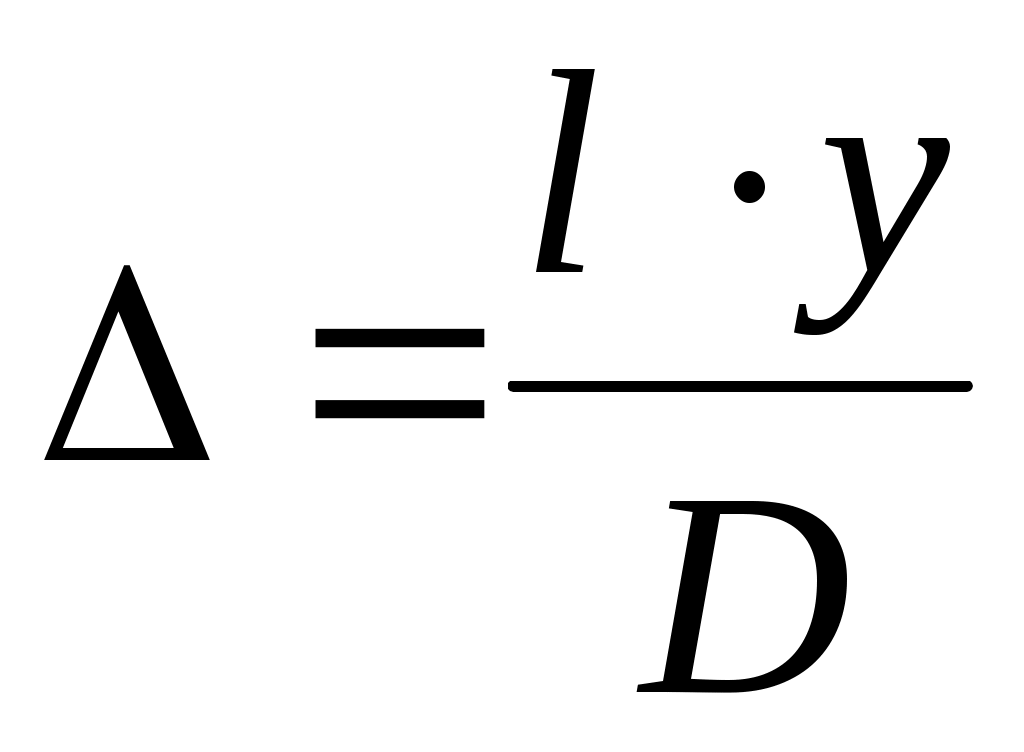 (8) (8)
Пользуясь условием (4), при котором получается максимум интенсивности на экране, находим:
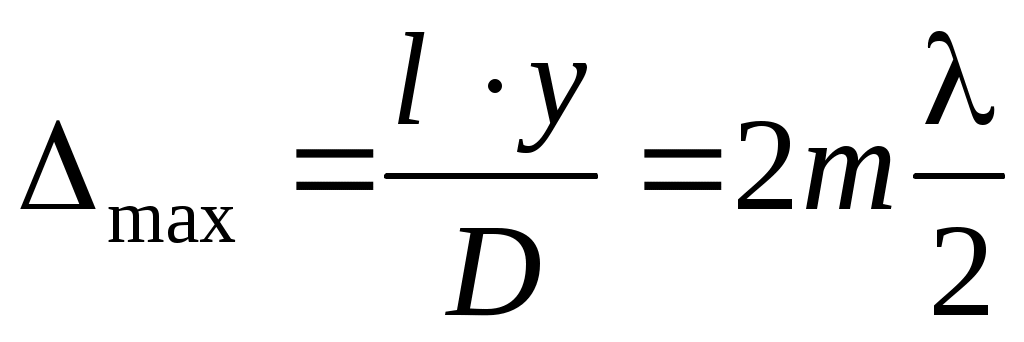 ; (9) ; (9)
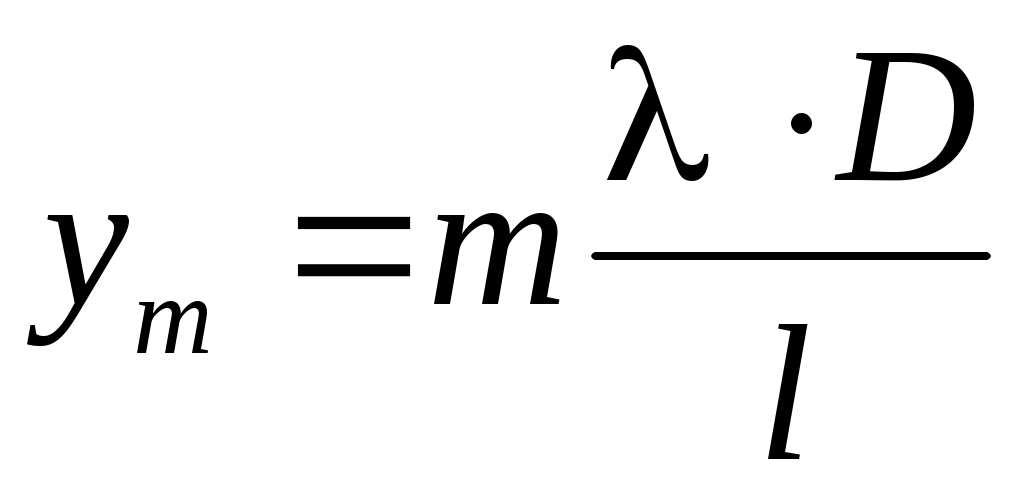 . (10) . (10)
Соотношение (10) показывает, что максимумы отстоят друг от друга на равных расстояниях. Обозначая расстояние, соответствующее одному из максимумов ym, а следующему ym+1, получим:
 . (11) . (11)
2. Описание установки
2.1. Определение длины световой волны с помощью бипризмы Френеля
Лабораторная установка (рис.4) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), короткофокусной собирающей линзы с фокусным расстоянием f1= 1 см (3), бипризмы Френеля (4) и экрана (5). Все элементы установлены на оптической скамье (6).
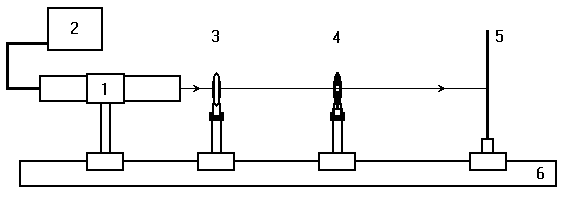
Рис. 4. Схема лабораторной установки
2.2. Получение увеличенного изображения интерференционной картины
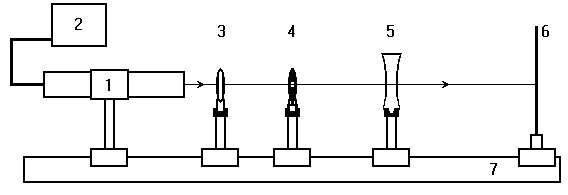
Рис. 5. Схема лабораторной установки
Лабораторная установка (рис.5) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), короткофокусной собирающей линзы (3) с фокусным расстоянием f1= 1 см, бипризмы Френеля (4), рассеивающей линзы (5) с фокусным расстоянием f2= -11 см, и экрана (6). Все элементы установлены на оптической скамье (7).
Линзы закреплены в оправах и устанавливаются в рейтеры, которые могут перемещаться вдоль оптической скамьи. Положение всех элементов на скамье определяется с помощью шкалы, прикрепленной к оптической скамье, или линейки. Все оптические детали центрируются, т.е. должны быть установлены так, чтобы их центры лежали на одной высоте, оптические оси линз были параллельны ребру оптической скамьи, плоскость экрана была перпендикулярна оптической оси линз.
3. Порядок выполнения работы
3.1. Установить оптические элементы согласно рис.4. Включить лазер.
3.2. Съюстировать линзу (3) по лучу лазера. Луч должен проходить вдоль главной оптической оси линзы. Это можно проконтролировать по отражению от поверхности линзы: отраженный луч должен попадать в выходное отверстие лазера. При этом лазерный пучок собирается в точку в фокальной плоскости.
3.3. Установить бипризму на расстоянии a
8–10 см от точки фокуса линзы. Расположить ее так, чтобы ребро бипризмы находилось в середине расфокусированного пятна.
3.4. Установить экран на расстоянии b
100 см от бипризмы. На экране будет наблюдаться интерференционная картина, образованная двумя когерентными пучками, идущими от мнимых источников, расстояние l между которыми вычисляется по формуле:
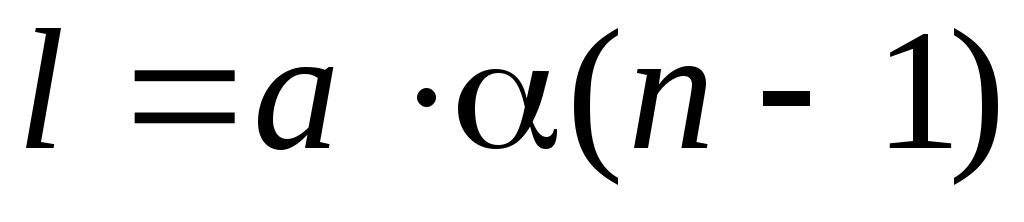 , (12) , (12)
где a - угол между преломляющей гранью и основанием бипризмы (a = 20/ = 5,8.10-3 рад).
Измерить ширину интерференционной полосы Dy (расстояния между соседними максимумами) не менее трёх раз. С целью увеличения точности измерения Dy нужно определять расстояние между максимально удаленными друг от другаi-й и k-й интерференционными полосами и делить его на 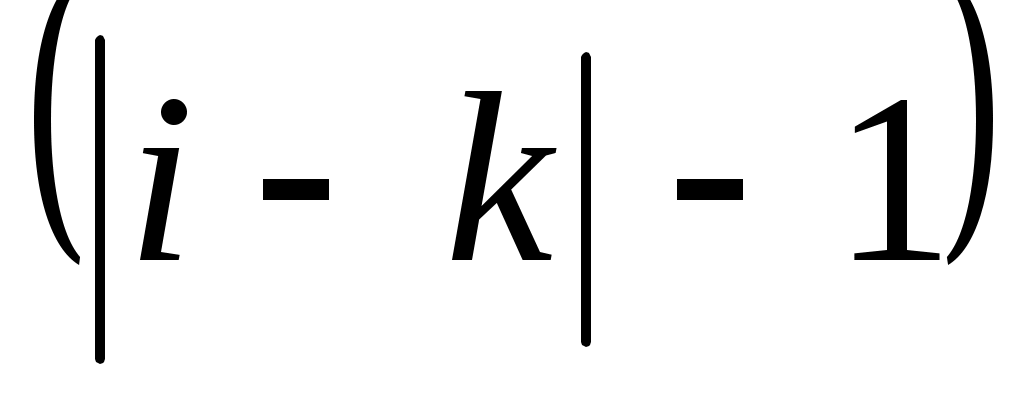 . .
По формуле:
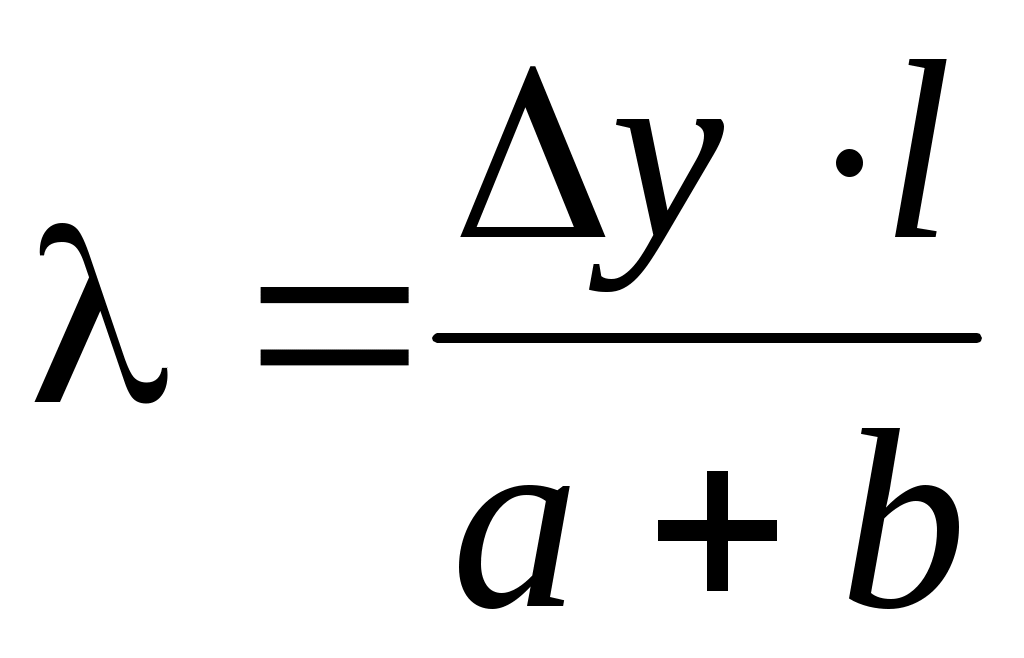 (13) (13)
определить длину волны l излучения лазера для различных значений Dy.
3.7. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.8. Установить оптические элементы согласно рис.5. Получить увеличенную интерференционную картину. Ширина интерференционной полосы при наличии рассеивающей линзы будет определяться выражением:
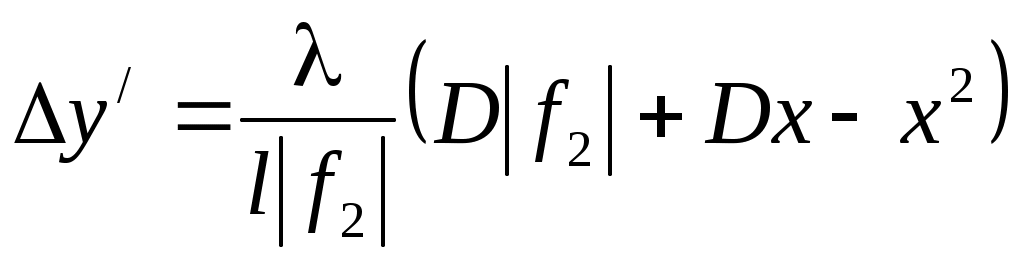 , (14) , (14)
где x - расстояние между мнимыми источниками и рассеивающей линзой, D - расстояние между экраном и мнимыми источниками. Измерить Dy’ при разных положениях линзы не менее трёх раз.
3.9. Определить из формулы (14) длину волны лазера для различных значений Dy’. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.10. Сравнить полученный результат с истинной длиной волны лазера и со значением, полученным в п.3.7.
4. Контрольные вопросы и задания
В чем состоит классический опыт Юнга по наблюдению интерференционной картины? Из какого условия находятся минимальные и максимальные значения интенсивности на экране для этого случая?
Что называется интерференцией?
В результате интерференции каких волн получается четкая интерференционная картина?
Как связаны между собой когерентность и монохроматичность световых волн?
Может ли наблюдаться интерференционная картина в солнечном свете?
Какие существуют способы получения когерентных волн в оптике?
Объясните принцип действия билинзы Бийе, бизеркал Френеля, зеркала Ллойда?
Точечный монохроматический источник света (l = 0,5 мкм) расположен на оси симметрии бипризмы Френеля, перпендикулярной наибольшей стороне, на расстоянии 0,1 м от бипризмы, а плоский экран находится на расстоянии 2,9 м от бипризмы. Сколько белых и темных полос образуется на экране (угол a при вершине бипризмы составляет 20’, толщиной бипризмы в расчетах можно пренебречь)?
Найдите распределение интенсивности на экране в установке с зеркалами Френеля. Интерферирующие лучи падают на экран приблизительно перпендикулярно его поверхности.
Найдите ширину полос интерференции в установке с зеркалом Ллойда, если известна длина волны излучения, расстояние от вторичных источников до экрана и расстояние от источника до зеркала.
Лабораторная работа
КОЛЬЦА НЬЮТОНА
ЦЕЛЬ РАБОТЫ: изучение явления интерференции в тонких клиньях с помощью колец Ньютона (полосы равной толщины), определение радиуса кривизны линзы и длины световой волны с помощью такой интерференционной схемы.
ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, ртутная лампа, оптическая скамья, набор светофильтров, микроскоп, волоконный световод, система «линза-пластинка» для наблюдения колец Ньютона.
1. Теоретическая часть [1¸6]
1.1. Виды интерференционных полос
Происхождение интерференционной картины и способ ее получения определяют вид интерференционных полос, представляющих собой чередующиеся максимумы и минимумы интенсивности света.
Пусть интерференционное устройство представляет собой слой прозрачного диэлектрика с частично отражающими и пропускающими поверхностями, в котором возникает геометрическая разность хода D при произвольном угле падения j света на это устройство. К такому типу интерферометров можно отнести плоскопараллельные и клиновидные диэлектрические пластины (например, интерференция в тонких пленках, кольца Ньютона и др.), а также интерферометры, расщепляющие пучки с помощью зеркал (интерферометр Майкельсона и его аналоги, эталон Фабри-Перо). Здесь можно рассмотреть три вида интерференционных полос, получающихся при следующих условиях:
l = const; j = const. При вариации геометрической разности хода имеют место полосы равной толщины.
l = const; D = const. При вариации угла падения получаем полосы равного наклона.
j = const; D = const. При вариации длины волны получаем полосы равного хроматического порядка.
Полосы равной толщины возникают в том случае, если интерферирующие пучки после прохождения интерференционной системы имеют реальное или мнимое пересечение в пространстве изображений.
Полосы равного наклона возникают между параллельными пучками света, которые после прохождения интерферометра приобретают определенную разность хода.
Полосы равного хроматического порядка в интерференционных схемах используется крайне редко (для очень точных измерений толщины плоскопараллельных пластин или воздушных промежутков).
1.2. Интерференция в тонких пленках
При распространении световой волны в среде уменьшается скорость распространения волны и соответственно ее длина, т.к. частота не изменяется. При расчете изменения фаз волны в среде в качестве длины пути удобнее брать оптическую длину пути, равную геометрической длине, умноженной на показатель преломления:
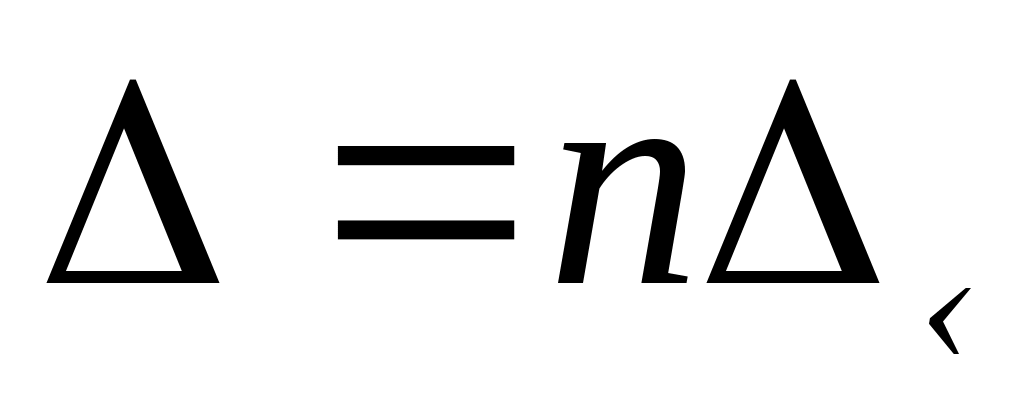 . (1) . (1)
Тогда длину волны и волновой вектор в формулах можно задавать равными их значениям в вакууме. Аналогично (1) вводится и связь между геометрической и оптической разностью хода.
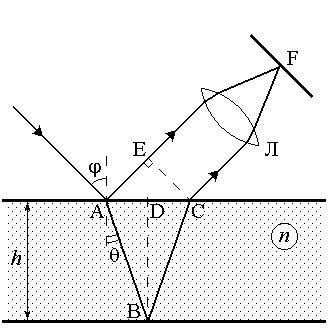
Рис.1
Полосы равного наклона. Рассмотрим случай, когда плоская монохроматическая волна падает под углом j на поверхность плоскопараллельной пластинки с относительным показателем преломления n и толщиной h(рис.1). Интерференция возникает между двумя волнами, отраженными от верхней и нижней поверхностями пластины. Так как эти пучки параллельны между собой, то интерференция наблюдается (локализована) или на бесконечности, или в фокальной плоскости Fлинзы Л. С учетом потери полволны на границе раздела сред (если n> 1, то в точке A, если n< 1, то в точке B) оптическая разность хода в данном случае равна
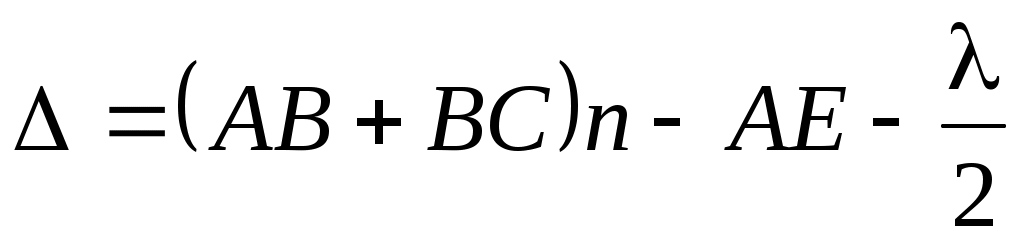 . (1) . (1)
Проведем ряд несложных преобразований для нахождения оптической разности хода.
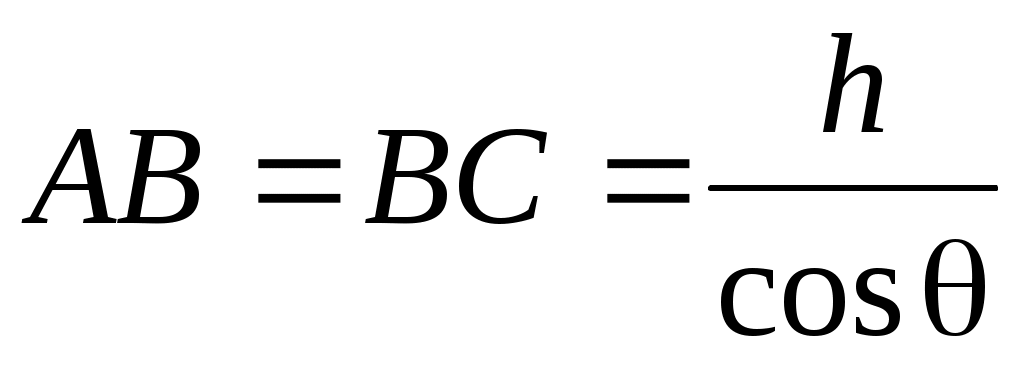 . (2) . (2)
Тогда
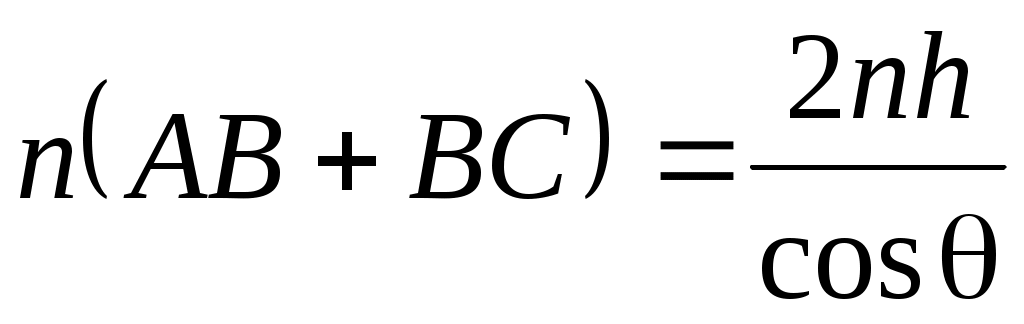 . (3) . (3)
Далее,
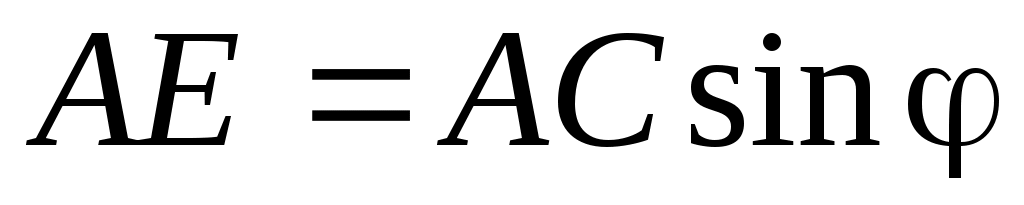 . (4) . (4)
Но
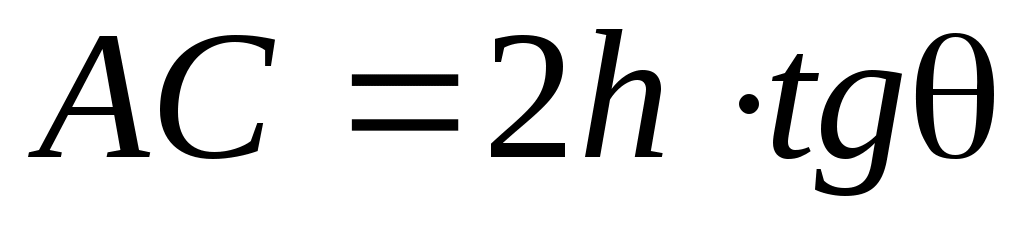 . (5) . (5)
Поэтому
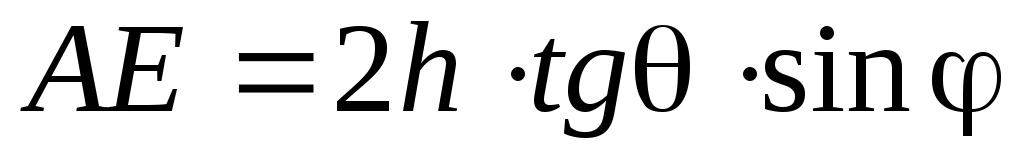 . (6) . (6)
Тогда:
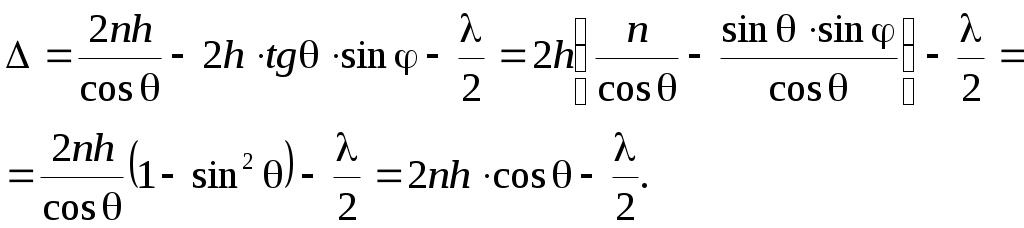 (7) (7)
Здесь учтена связь из закона Снеллиуса углов падения j и преломления q:
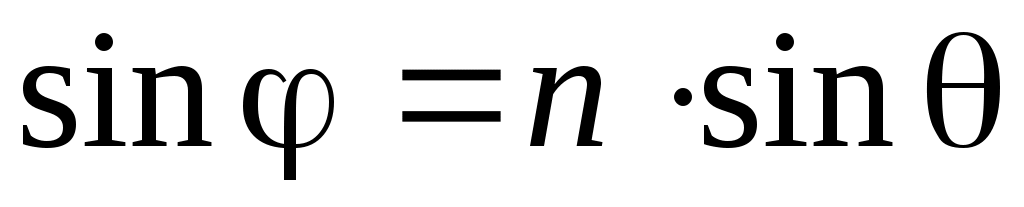 . (8) . (8)
Таким образом, получаем для оптической разности хода:
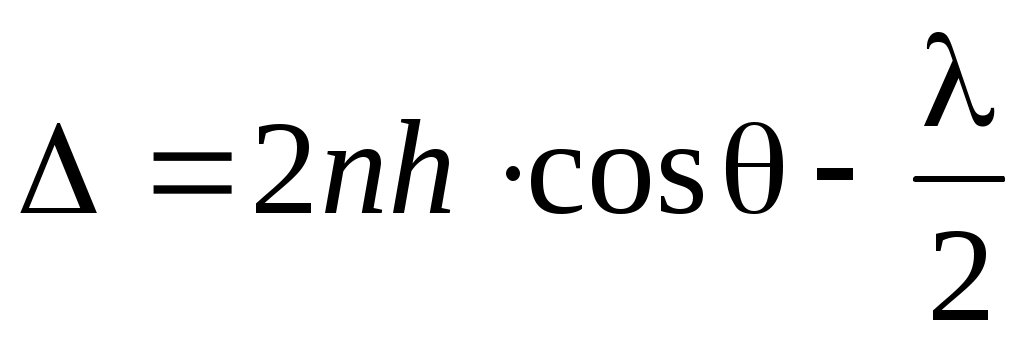 . (9) . (9)
Условием максимума интерференционной картины является (см. лабораторную работу «Бипризма Френеля»:
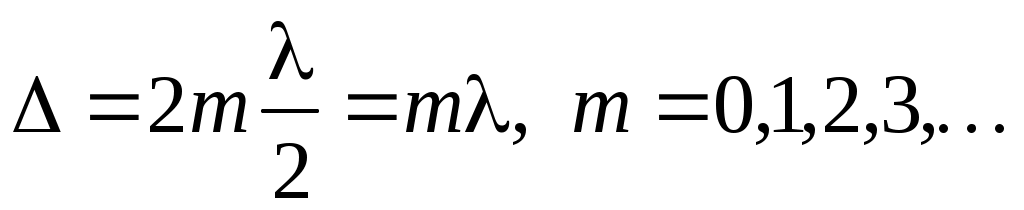 . (10) . (10)
а условием минимума –
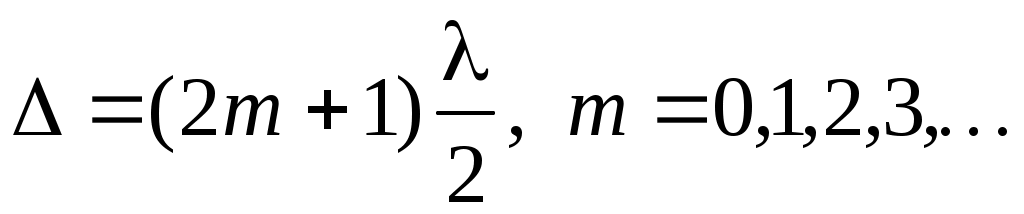 (11) (11)
Если на пластинку падают непараллельные пучки света, то и интерферирующие пучки будут иметь все всевозможные направления распространения. При заданных толщине пластины и показателе преломления каждому углу падения волны соответствует своя интерференционная полоса. Поэтому такие полосы и называют полосами равного наклона. При аксиально симметричном распределении падающих пучков линии равного наклона являются окружностями.
Даже если источник света протяженный, и различные его точки излучают некогерентно, интерференционные картины не зависят от фазы волны в точке расщепления пучков на поверхности пластины (точка A на рис.1) и от положения этой точки, а зависят лишь от угла падения. Поэтому конечность размеров источника не смазывает картину полос равного наклона и не является ограничивающим интерференцию фактором.
Если падающий свет не монохроматичный, при увеличении разности длин падающих волн интерференционные кольца разделяются и при некотором значении этой разности полосы соседних порядков перекрываются. Разность длин волн, при которой наступает перекрытие полос соседних порядков интерференции, называется дисперсионной областью(или областью свободной дисперсии). Увеличение толщины пластины уменьшает дисперсионную область. Для наблюдения интерференции в белом свете толщина должна быть достаточно малой (
10 мкм). Поэтому в данном случае речь идет об интерференции в тонких пленках.
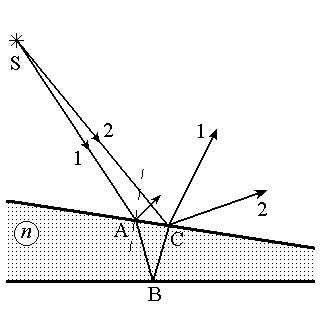
Рис. 2
Полосы равной толщины. Теперь рассмотрим интерференцию света на пластинке с переменной толщиной (клине) (рис.2). В световом потоке, исходящем из источника S монохроматического света всегда присутствует волна 2, интерферирующая в точке C с волной 1, прошедшей по пути SABC. Если источник расположен достаточно далеко от поверхности клина и угол между поверхностями клина достаточно мал (эти условия на практике при изучении такой схемы интерференции, как правило, выполняются), то оптическая разность хода приблизительно определяется при прочих равных условиях толщиной клина в точке Cи высчитывается по той же формуле, что и (9). Однако в этом случае интерференционная картина локализована на верхней поверхности клина. Интерференционную картину можно также наблюдать и с помощью линзы на экране. В этом случае поверхность проецируется на экран наблюдения. Линии одинаковой интенсивности совпадают с линиями постоянной толщины пластины, поэтому соответствующие интерференционные полосы называются полосами равной толщины. Ограничения на толщину клиновидной пластины, связанные со степенью временной когерентности (или монохроматичности) такие же, как и в случае плоскопараллельной пластины.
1.3. Кольца Ньютона
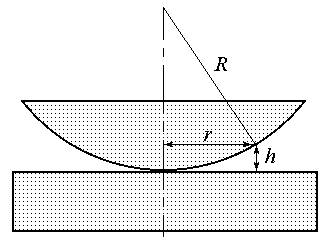
Рис. 3
Примером интерференционной схемы, в которой наблюдаются полосы равной толщины, является воздушная прослойка, образованная между плоской поверхностью стекла и положенной на нее плосковыпуклой линзой (или наоборот) (рис.3). В этом случае линии равной толщины – окружности, поэтому интерференционная картина имеет вид концентрических колец. Потеря полволны происходит на нижней поверхности воздушного клина. Пусть h – толщина воздушного клина в точке минимума картины (темное кольцо), R – радиус кривизны линзы. Найдем радиус темного интерференционного кольца m-го порядка. Из геометрии рисунка видно, что
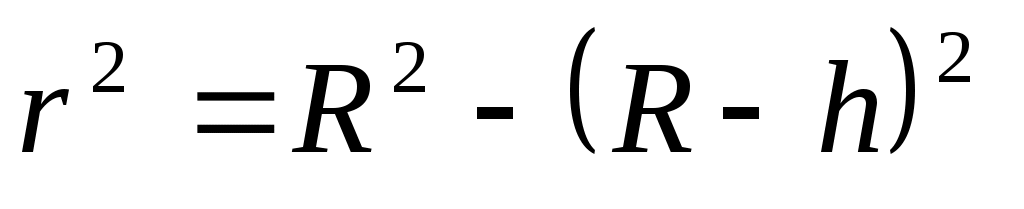 . (12) . (12)
Учитывая, что 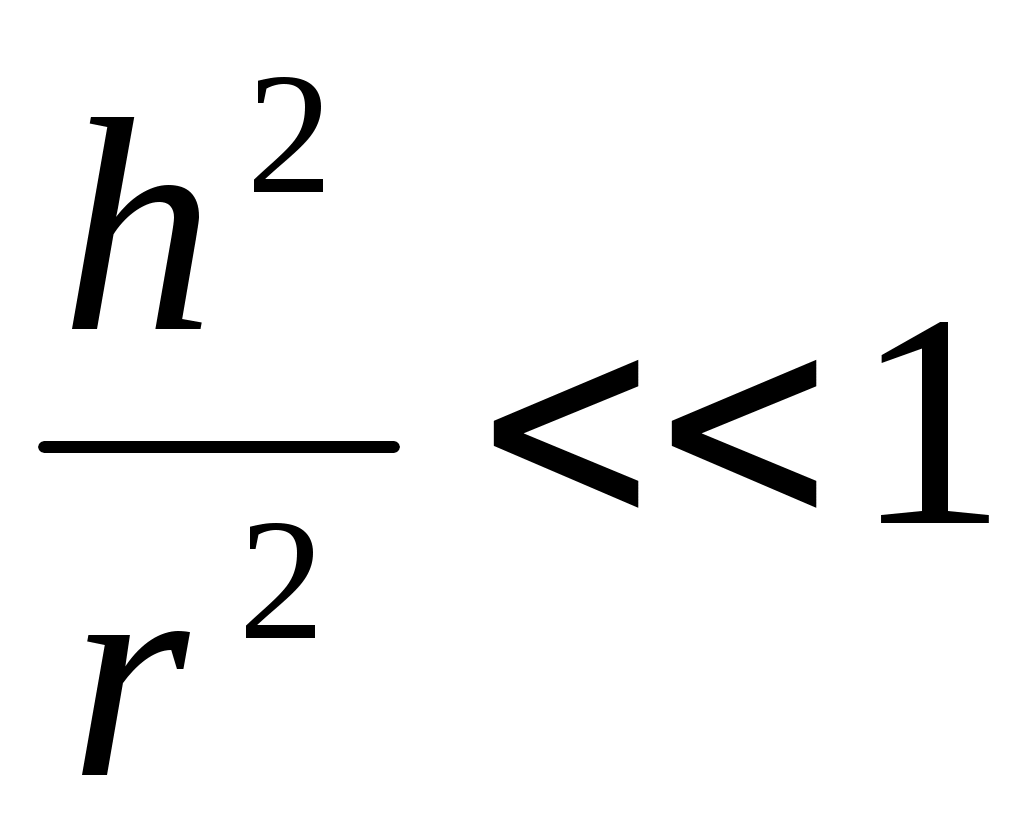 , получаем , получаем 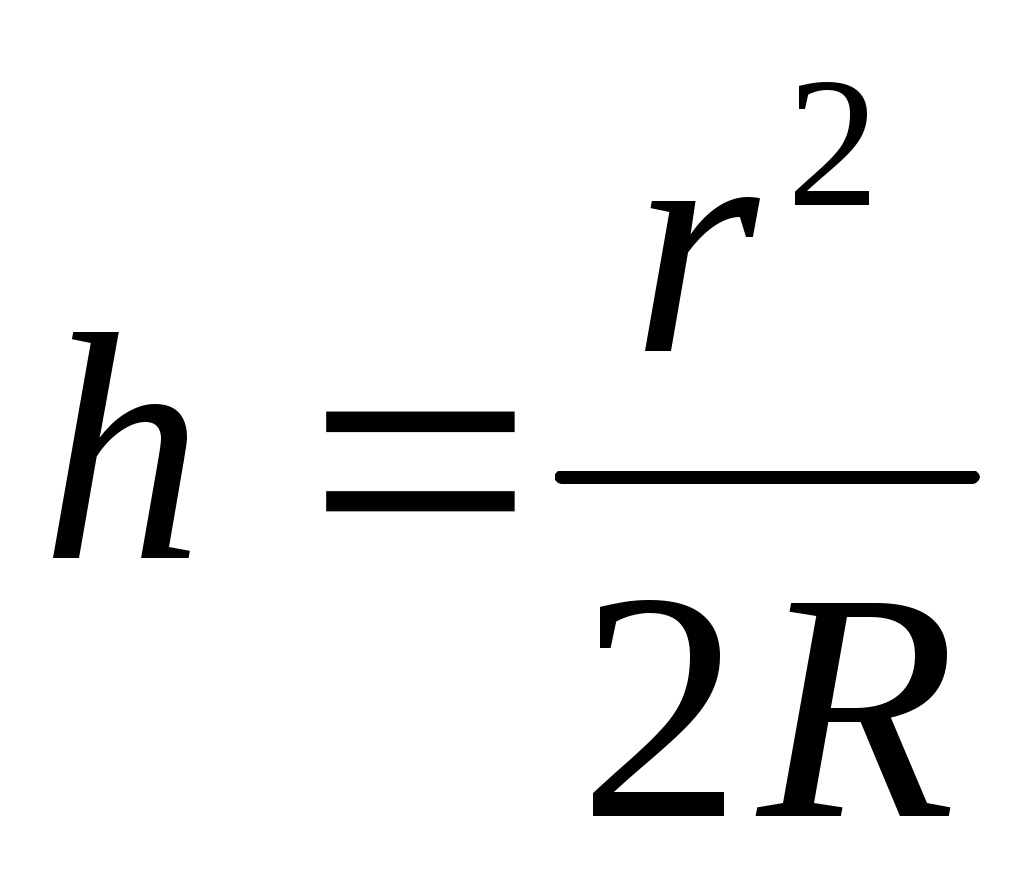 . Используя условие минимума (11), получаем для радиуса m-го темного кольца: . Используя условие минимума (11), получаем для радиуса m-го темного кольца:
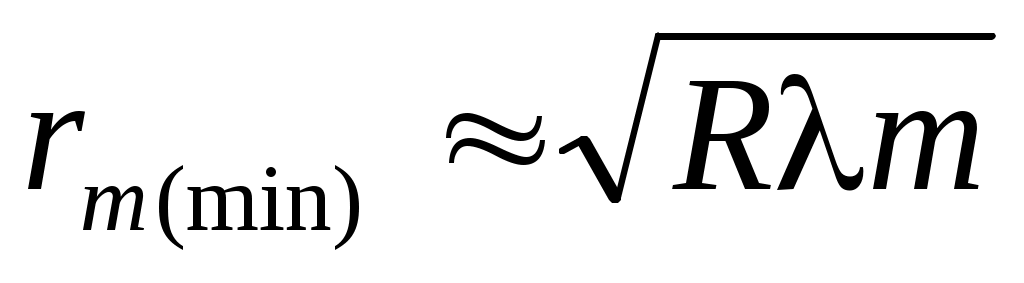 . (13) . (13)
Отметим, что используя условие максимума (10), аналогично можно получить выражение для радиуса m-го светлого кольца:
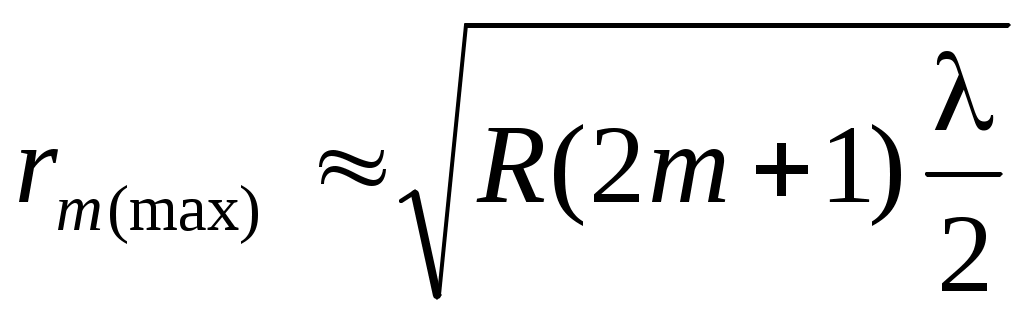 . (14) . (14)
Следовательно, измерив радиус m-го интерференционного кольца и зная радиус кривизны линзы, можно определить длину волны света (или решить обратную задачу).
Интерференционные кольца наблюдаются как в отраженном, так и в прошедшем свете. При этом там, где в отраженном свете наблюдается светлое кольцо, в прошедшем – темное, т.е. интерференционные картины в прошедшем и отраженном свете являются взаимно дополнительными. Центральное пятно в отраженном свете – темное, т.к. толщина воздушного клина пренебрежимо мала, и волны интерферируют практически в противофазе из-за потери полволны. В белом свете, как и следует из формул (13, 14), наблюдаются цветные кольца.
Контрастность интерференционных картин в отраженном и прошедшем свете неодинакова. Для наблюдения четкой интерференционной картины в отраженном свете поверхности клина должны обладать малым коэффициентом отражения, а в прошедшем – большим. Это легко видеть из соотношений амплитуд интерферирующих волн, которые для лучшей видимости должны стремиться к единице. Для отраженных волн оно равно 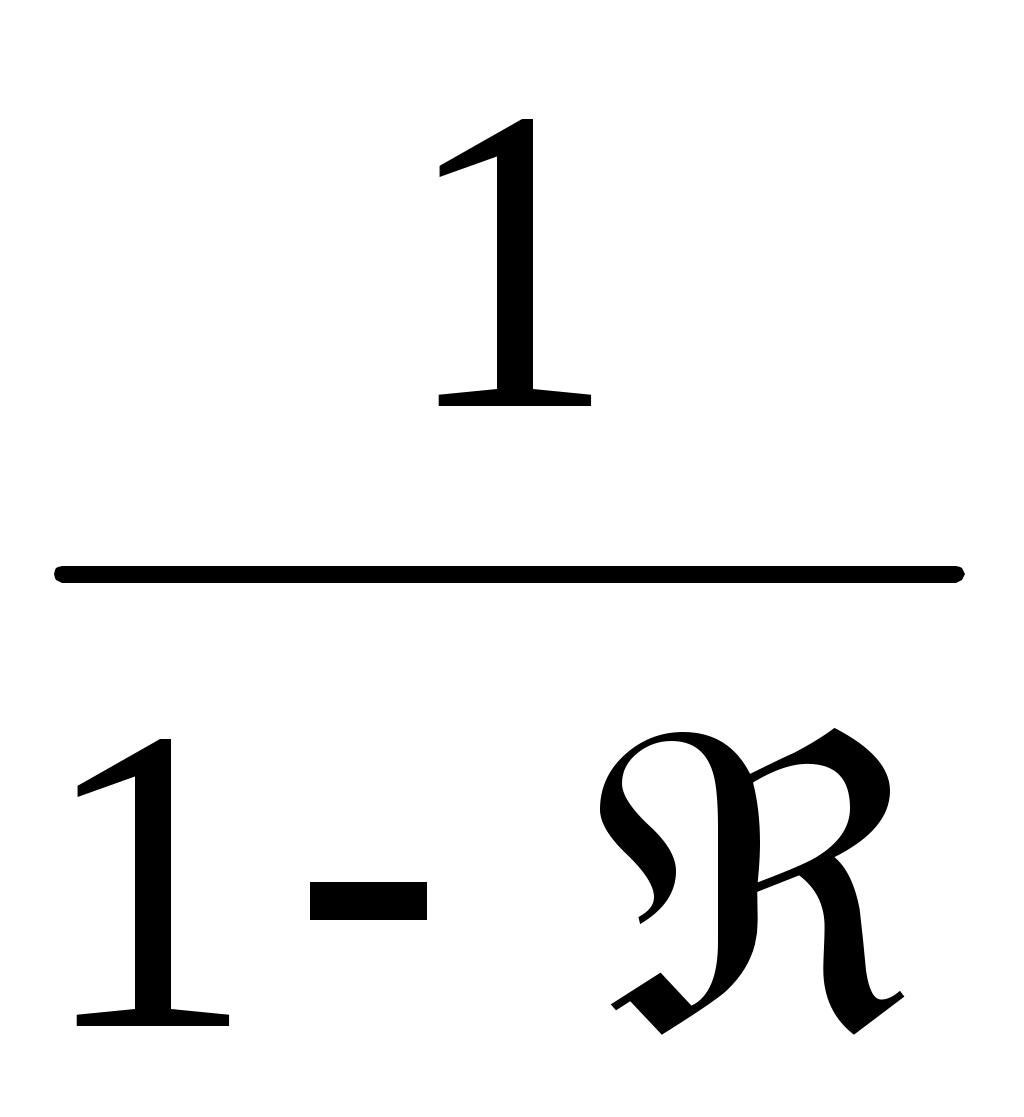 , а для прошедших – , а для прошедших – 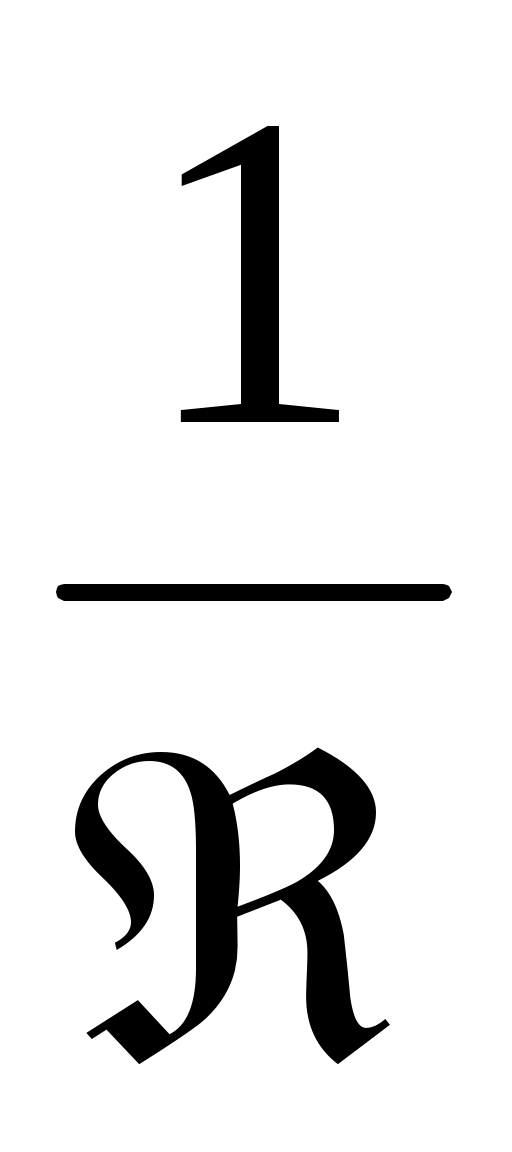 , где Â – энергетический коэффициент отражения. , где Â – энергетический коэффициент отражения.
2. Описание установки
Лабораторная установка (рис. 4) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), ртутной лампы ((3) – излучатель, (4) – источник питания лампы), стеклянных светофильтров (5), бинокулярного микроскопа МБС-9, световода (6), закрепленного в оправе (7), системы «линза-пластинка» (9). Все оптические элементы размещены на оптической скамье (8). По световоду свет через один из окуляров попадает на систему «линза-пластинка», помещенную на предметном столике (10) микроскопа. Для измерения диаметра колец Ньютона используется шкала, закрепленная в окуляре микроскопа. При положении «4» на шкале увеличений (11) объектива микроскопа, цена малого деления окуляра составляет 0,25 мм. При помощи ручки (12) осуществляется фокусировка микроскопа на объект. Открепив винт (13), можно вращать при необходимости оптическую головку (14) на 180° в горизонтальной плоскости.
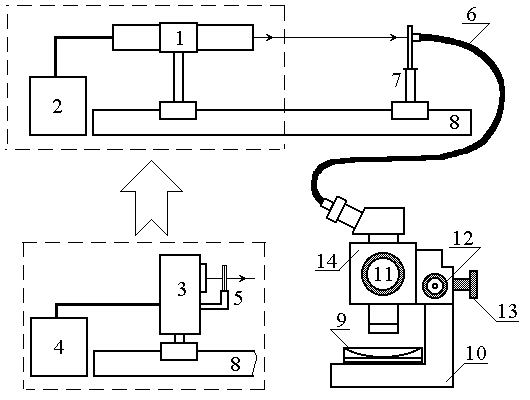
Рис. 4. Схема лабораторной установки
3. Порядок выполнения работы
3.1. Определение радиуса кривизны линзы
3.1.1. Поставить в положение «4» шкалу (11) объективной части микроскопа и не менять этого положения в процессе всей работы.
3.1.2. Включить лазер тумблером на панели блока питания, при этом должна загореться лампочка рядом с тумблером. Через 1-2 с. начнется генерация лазерного излучения.
3.1.3. Направить излучение лазера на входное отверстие световода.
3.1.4. Глядя в окуляр микроскопа, совместить центр интерференционной картины с центром поля окуляра, осторожно перемещая систему «линза-пластинка» на предметном столике.
3.1.5. Перемещая световод по полю окуляра, снять отсчеты в точках пересечения 3, 4, 5, 6, 7-го темных колец со шкалой пять раз. Номера колец отсчитываются от центра интерференционной картины в направлении увеличения значений шкалы
3.1.6. Повторить п.3.1.5., отсчитывая номера колец, в направлении уменьшения значений шкалы
3.1.7. Определить диаметры 3, 4, 5, 6, 7-го темных колец как разность соответствующих отсчетов в обоих направлениях с учетом цены малого деления окуляра.
3.1.8. Найти среднее значение диаметра для каждого кольца.
3.1.9. Определить радиус кривизны линзы по формуле
Rn+1, n= (D2n+1 – D2n) / 4λлаз (15`)
где n = 3, 4, 5, 6.
3.1.10. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.2. Определение длин волн ртутного спектра по кольцам Ньютона
3.2.1. Заменить лазер ртутной лампой. Закрыть окно кожуха лампы светофильтром, выделяющим зеленую линию ртутного спектра. Для этого использовать сразу два фильтра ПС-7 и ЖС-17 (или аналогичные, указанные преподавателем).
3.2.2. Проделать п.п. 3.1.4.–3.1.8. Определить длину волны зеленой линии ртутного спектра, используя найденное выше значение Rср и формулу (15`).
3.2.3. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.2.4. Проделать п.п. 3.2.1.–3.2.3., выделив из ртутного спектра желтую, синюю линии, используя при этом фильтры ОС-13, ЖЗС-18 и ПС-11, ЖС-11 соответственно (или аналогичные, указанные преподавателем).
3.2.5. Занести результаты в таблицу 1.
Таблица 1. Определение радиуса кривизны линзы по темным кольцам Ньютона
nтемного кольца
|
Отсчет по шкале
|
D
мм
|
Dср
мм
|
σD
мм
|
R n+1, n
мм
|
Rср
мм
|
σR
мм
|
∆R
мм
|
в направлении увеличения значений
|
в направлении уменьшения значений
|
3
|
|
|
|
|
|
______
______
______
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2. Определение длин волн ртутного спектра по темным кольцам Ньютона
nтемного кольца
|
Отсчет по шкале
|
D
мм
|
Dср
мм
|
σD
мм
|
R n+1, n
мм
|
λn+1, n
нм
|
λ ср мм
|
σλ мм
|
∆λ мм
|
в направлении увеличения значений
|
в направлении уменьшения значений
|
3
|
|
|
|
|
|
______
______
______
|
______
______
______
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Контрольные вопросы и задания
1. Исходя из формул Френеля, описать поведение фаз отраженной и преломленной волн при изменении угла падения световой волны на границе раздела двух диэлектриков. Рассмотреть все случаи (s- и p- поляризация падающей волны, падение в оптически более плотную среду и наоборот).
2. На основании задания № 2 рассмотреть результирующее изменение фазы для волны, которая падает из воздуха сверху на стеклянную пластинку и, отразившись от нижней грани этой пластинки, выходит через верхнюю грань обратно в воздух.
3. То же, что и в задании № 3, только пластинка находится в среде, более оптически плотной.
4. Найти радиус r центрального темного пятна колец Ньютона, если между линзой и пластинкой, изготовленных из стекла с показателем преломления n = 1,6 налит бензол (nБ= 1,5). Радиус кривизны линзы R = 1 м. Наблюдение ведется в отраженном натриевом свете (l = 589 нм).
5. Кольца Ньютона получаются между двумя плосковыпуклыми линзами, прижатыми друг к другу своими выпуклыми поверхностями. Найти радиус m-го темного кольца, если длина световой волны равна l, а радиусы кривизны выпуклых поверхностей линз равны R1 и R2 . Наблюдение ведется в отраженном свете.
6. Кольца Ньютона получаются с помощью плосковыпуклой линзы с радиусом кривизны R1 , положенной на вогнутую сферическую поверхность с радиусом кривизны R2 > R1 . Кольца наблюдаются в отраженном свете. Определить радиус m-го темного кольца, если длина световой волны l задана.
7. Почему центр колец Ньютона, наблюдаемых в отраженном свете, обычно темный?
8. Зимой на стеклах трамвая и автобусов образуются тонкие пленки, окрашивающие все видимое сквозь них в зеленоватый цвет. Оценить, какова наименьшая толщина этих пленок (показатель преломления наледи принять равным 1,33).
9. Темной или светлой будет в отраженном свете мыльная пленка толщиной h = 0,1l? Пленка (n = 1,33) находится в воздухе.
10. Написать условия максимума и минимума полос равного наклона, наблюдаемых в фокальной плоскости объектива, помещенного в пучок лучей, прошедших сквозь плоскопараллельную пластинку?
11. В очень тонкой клиновидной пластинке с показателем преломления n = 1,5 в отраженном свете (l = 580 нм) при нормальном падении наблюдаются интерференционные полосы. Расстояние между соседними темными полосами x = 5 мм. Найти угол a между гранями пластинки.
12. Найти фокусное расстояние f плоско-выпуклой линзы, примененной для получения колец Ньютона, если радиус третьего светлого кольца равен 1,1 мм; показатель преломления стекла n = 1,6; l = 580 нм. Кольца наблюдаются в отраженном свете.
13. Оценить по порядку величины толщину нефтяной пленки, которая образовалась из пролитой нефти на поверхности воды. Рассмотреть для этого наблюдаемые цвета тонкой пленки, которые возникают при освещении ее источником белого света.
14. Почему кольца Ньютона, наблюдаемые в данной лабораторной работе, более контрастны в отраженном, а не в проходящем свете?

|
|
|
 Скачать 5.21 Mb.
Скачать 5.21 Mb.



 . (6)
. (6)
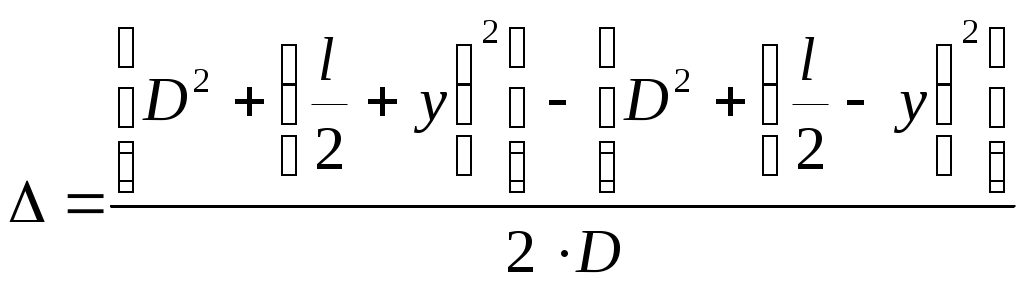 (7)
(7)


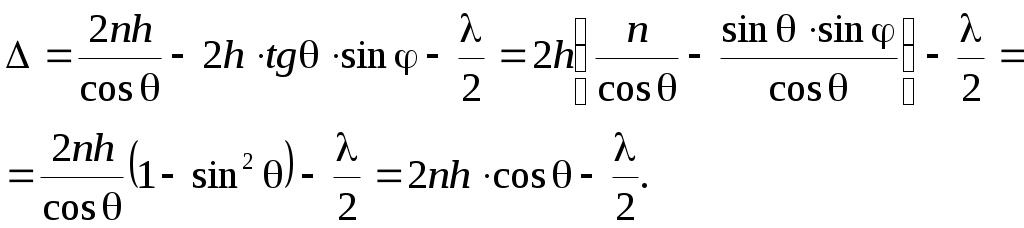 (7)
(7)

