|
|
лабораторный практикум. Практикум волгоград 2014 Печатается по решению редакционноиздательского совета
ДИФРАКЦИЯ СВЕТА
Лабораторная работа
ЗОНЫ ФРЕНЕЛЯ
ЦЕЛЬ РАБОТЫ: изучение дифракции Френеля на круглом отверстии и свойств зонной пластинки.
ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, металлическая пластинка с набором круглых отверстий различных диаметров, две собирающие линзы, зонная пластинка, экран, линейка, оптическая скамья с набором рейтеров.
1. Теоретическая часть [1¸6]
1.1. Принцип Гюйгенса-Френеля
Под дифракцией света обычно понимают отклонения закономерностей распространения света от законов, предписываемых геометрической оптикой. В явлениях дифракции, как и в явлениях интерференции, проявляются волновые свойства света. Дифракцию можно наблюдать, например, когда на пути распространения света находятся препятствия, т.е. непрозрачные тела произвольной формы (экраны) или когда волновой фронт искусственно ограничен. Тщательный опыт показывает, что вместо резкой границы между светом и тенью (как предсказывает геометрическая оптика) получается сложная картина распределения освещенности, состоящая из темных и светлых участков – дифракционных полос. Теория дифракции света дает строгое обоснование геометрической оптике и определяет условия ее применимости. Математически строгое решение дифракционных задач на основе волнового уравнения (или уравнений Максвелла) с граничными условиями, зависящими от характера препятствий, как правило, представляет значительные трудности. Поэтому применяются приближенные методы решения задачи о распределении света вблизи границы между светом и тенью, основанные на принципе Гюйгенса – Френеля.
Пусть A – источник света, а s – произвольная замкнутая поверхность, охватывающая A. Согласно принципу Гюйгенса – Френеля,в любой точке, находящейся вне поверхности s, световая волна, возбуждаемая источником A, может быть представлена как результат суперпозиции когерентных вторичных волн, которые «излучаются» элементарными источниками, непрерывно распределенными вдоль вспомогательной поверхности s. Иными словами, вне поверхности s распространяющаяся первичная волна может быть заменена системой когерентных вторичных волн, интерферирующих при наложении [1]. Принцип Гюйгенса-Френеля является приближением, наиболее пригодным для описания дифракции коротких волн (когда длина волны много меньше характерных размеров препятствий). При формулировке принципа не уточняются граничные условия для напряженностей электромагнитного поля (например, не различаются металлический и диэлектрический экраны) и не учитывается векторный характер поля. Для решения задач по нахождению распределения интенсивности света при дифракции на непрозрачных экранах с отверстиями делаются два предположения (граничные условия Кирхгофа) [2]:
непроницаемые части экрана не являются источниками вторичных волн;
в отверстии точки волнового фронта являются такими же источниками вторичных волн, какими они были бы при отсутствии непроницаемых частей экрана.
1.2. Зоны Френеля [2]
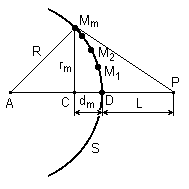
Рис. 1
Пусть A – источник сферической волны, S – волновой фронт в некоторый момент времени, R – радиус кривизны этого фронта (рис.1). Найдем интенсивность в точке P с помощью принципа Гюйгенса – Френеля. Разобьем поверхность S на кольцеобразные зоны такого размера, чтобы расстояния от краев зоны (в разрезе это соответствует точкам M1 ,M2 , …, Mm) до P отличались на l/2 (эти зоны называются зонами Френеля):
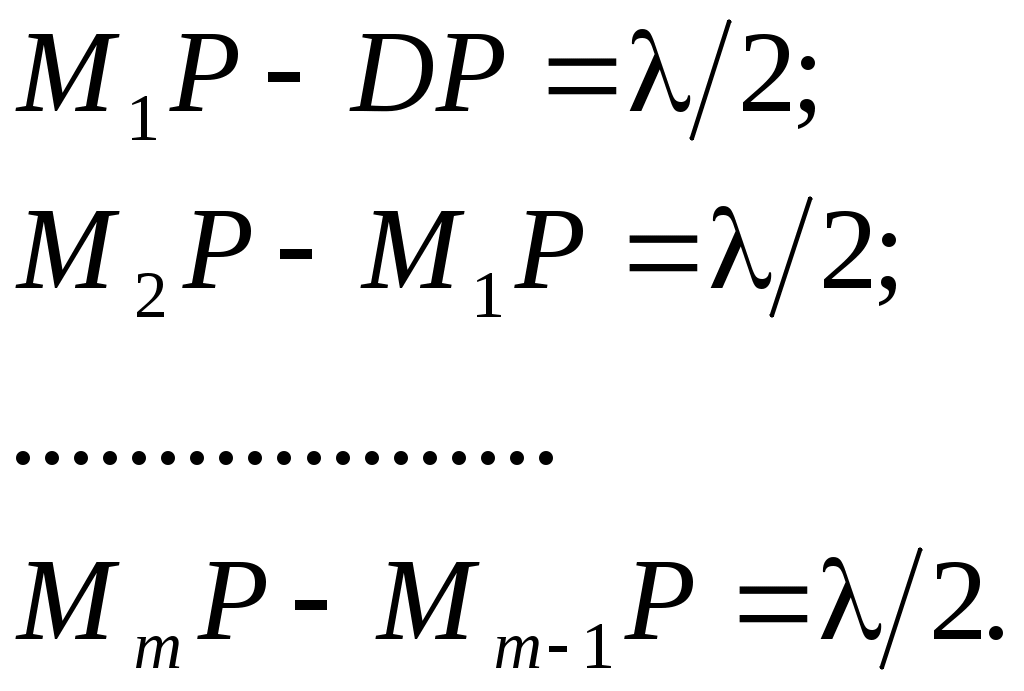 (1) (1)
Из рис.1 видно, что радиус m–й зоны Френеля rm (m=0;1;2;…) может быть получен из соотношения:
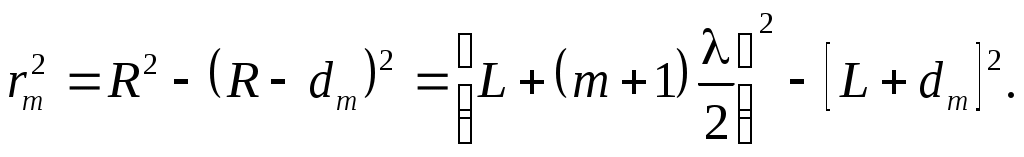 (2) (2)
Исключая величину dm и пренебрегая слагаемыми
l2 ввиду их малости, получаем:
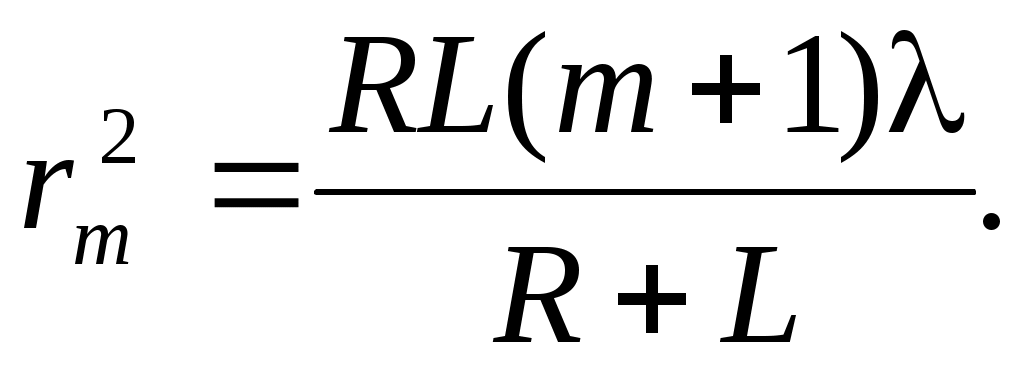 (3) (3)
Можно показать, что площади всех зон Френеля примерно одинаковы:
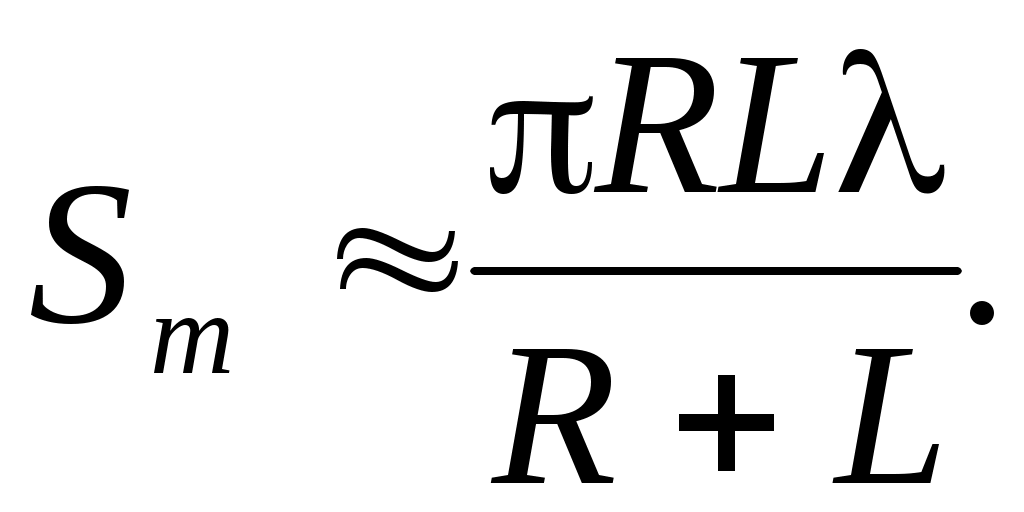 (4) (4)
В случае пренебрежения кривизной поверхности это не вносит существенной ошибки, если радиусы зон Френеля много меньше радиуса кривизны волнового фронта. Обычно это справедливо для очень большого числа зон Френеля.
1.3. Метод векторных диаграмм
Разделим каждую из зон, в свою очередь, на большое число N участков. Между началом и концом зоны фаза меняется на p, а между малыми участками – на d = p/N . Пусть E0 – амплитуда волны, приходящей в точку наблюдения P от каждого участка; а фаза волны, приходящей из точки D в точку P – равна нулю. Комплексная амплитуда волны в точке P от центральной зоны Френеля с учетом интерференции равна:
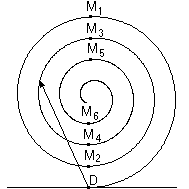
Рис. 2
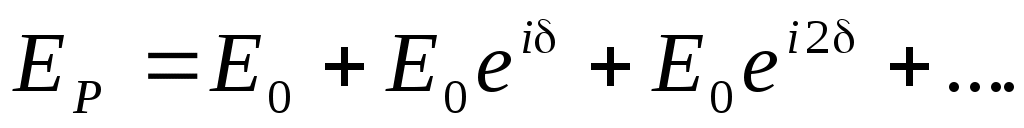 (5) (5)
Аналитическое сложение амплитуд можно заменить графическим построением, изображая комплексную амплитуду в виде вектора (рис.2). При увеличении числа разбиений до бесконечности ломаная кривая превращается в плавную. Длина вектора DM1 пропорциональна амплитуде волны в точке P, когда открыта вся центральная зона Френеля. Аналогично продолжая построение, можно получить кривую, по которой легко определить амплитуду волны (и ее интенсивность), зная соотношение диаметров открываемого отверстия и зон Френеля. При строгом равенстве амплитуд в (5) складываемых колебаний от элементарных участков результирующая амплитуда от двух открытых соседних зон была бы равна нулю, т.е. вторичные волны в результате интерференции погасили бы друг друга, но увеличение номера зоны приводит к уменьшению амплитуд вторичных волн (например, в (4) мы этим пренебрегли). Поэтому полученная кривая не замыкается, а имеет вид спирали. Зависимость амплитуды поля в точке P от радиуса отверстия показана на рис.3.

Рис. 3
Если на пути световой волны стоит непрозрачный круглый экран, то за экраном в его тени на оси возникает светлое пятно, называемое пятном Пуассона. Объяснение существования светлого пятна вытекает из рассуждений по методу зон Френеля. Экран закрывает некоторое число зон Френеля начиная с центральной. Однако следующие зоны после последней из закрытых создают в точке P освещенность, значение которой можно рассчитать с помощью спирали. Т.о., получается, что волна как бы огибает непрозрачный экран. Интенсивность пятна Пуассона весьма слаба при больших размерах непрозрачного экрана. Кроме того, необходимо, чтобы свет обладал достаточно большой степенью когерентности.
1.4. Зонная пластинка
Закроем все нечетные зоны, оставив открытыми четные (или наоборот). В результате получится пластинка, называемая зонной пластинкой. Из рис. 2 видно, что амплитуды поля в точке P будут определяться суммой сонаправленных векторов 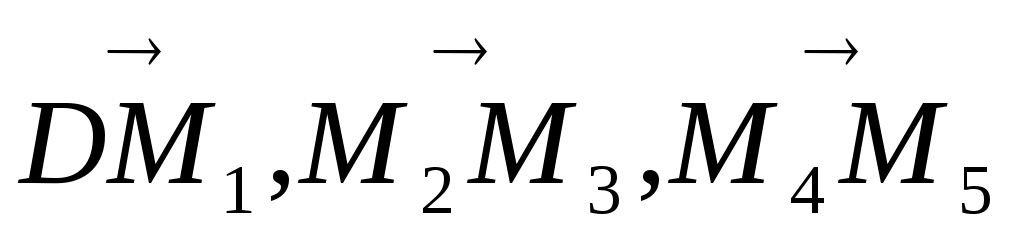 и т.д. Следовательно, в точке P на оси происходит значительное увеличение интенсивности света по сравнению с интенсивностью в точке P при полностью открытом фронте (примерно в m2 большее, чем дает отверстие в одну зону [3] ), т.е. в этой точке свет фокусируется, а зонная пластинка ведет себя как линза. Найдем фокусное расстояние f такой линзы. Будем считать, что лучи падают на зонную пластинку параллельно оси системы, т.е. R= ¥. Тогда точка P является фокусом. Формула (3) примет вид: и т.д. Следовательно, в точке P на оси происходит значительное увеличение интенсивности света по сравнению с интенсивностью в точке P при полностью открытом фронте (примерно в m2 большее, чем дает отверстие в одну зону [3] ), т.е. в этой точке свет фокусируется, а зонная пластинка ведет себя как линза. Найдем фокусное расстояние f такой линзы. Будем считать, что лучи падают на зонную пластинку параллельно оси системы, т.е. R= ¥. Тогда точка P является фокусом. Формула (3) примет вид:
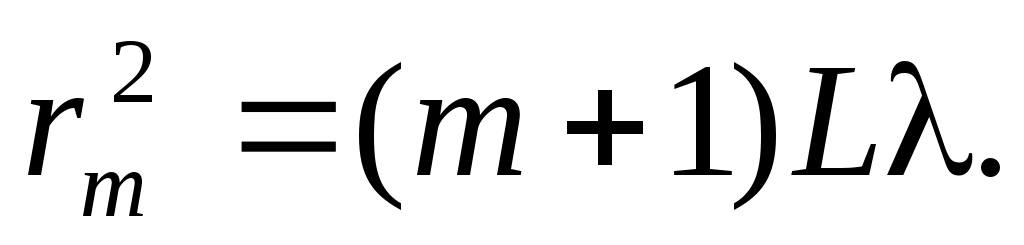 (6) (6)
Следовательно фокусное расстояние равно:
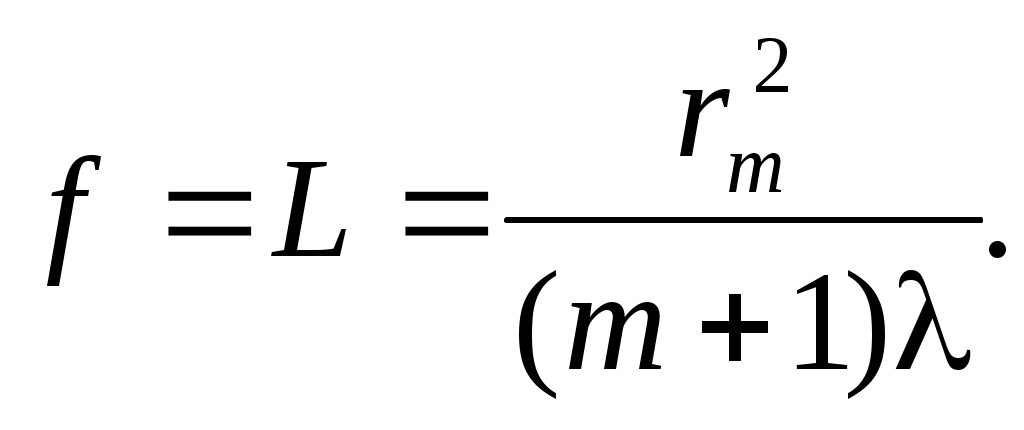 (7) (7)
Формула такой линзы принимает вид:
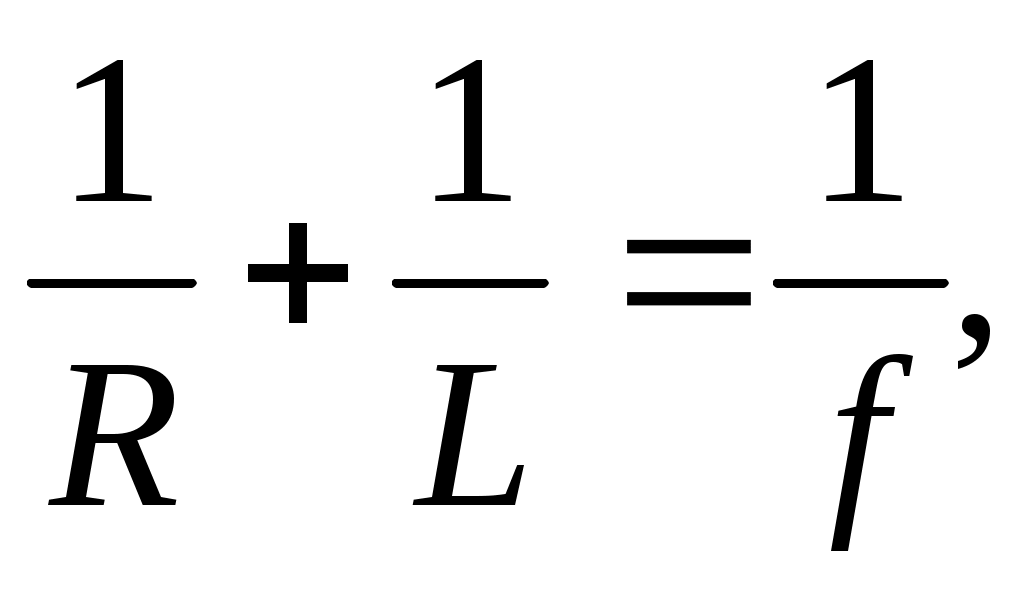 (8) (8)
т.е. аналогична известной формуле тонкой линзы. В отличие от обычной линзы зонная пластинка имеет несколько фокусов на оси системы в зависимости от количества открытых зон. Отметим, что и расположение зон Френеля на волновом фронте зависит от геометрии рассматриваемой системы.
2. Описание установки
2.1. Дифракция Френеля на круглом отверстии
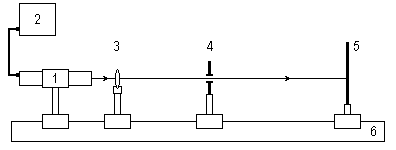
Рис. 4. Схема лабораторной установки
Лабораторная установка (рис.4) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), короткофокусной собирающей линзы (3) с фокусным расстоянием f1 = 1 см, металлической пластинки (4) с отверстиями диаметрами 1,59; 1,40; 1,13; 0,85; 0,71; 0,50 мм и экрана (5). Все элементы установлены на оптической скамье (6).
2.2. Изучение свойств зонной пластинки
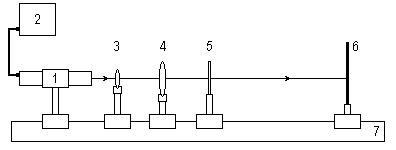
Рис. 5. Схема лабораторной установки
Лабораторная установка (рис.5) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), короткофокусной собирающей линзы (3) с фокусным расстоянием f1= 1 см, длиннофокусной собирающей линзы (4) с f2= 21 см, зонной пластинки (5) и экрана (6). Все элементы установлены на оптической скамье (7).
Линзы закреплены в оправах и устанавливаются в рейтеры, которые могут перемещаться вдоль оптической скамьи. Положение всех элементов на скамье определяется с помощью шкалы, прикрепленной к оптической скамье, или линейки. Все оптические детали центрируются, т.е. должны быть установлены так, чтобы их центры лежали на одной высоте, оптические оси линз были параллельны ребру оптической скамьи, плоскость экрана была перпендикулярна оптической оси линз.
3. Порядок выполнения работы
3.1. Установить оптические элементы согласно рис.4. Включить лазер.
3.2. Съюстировать линзу (3) по лучу лазера. Луч должен проходить вдоль главной оптической оси линзы. Это можно проконтролировать по отражению от поверхности линзы: отраженный луч должен попадать в выходное отверстие лазера. При этом лазерный пучок собирается в точку на фокальной плоскости.
3.3. Установить металлическую пластинку с отверстиями на расстоянии 5 – 25 см от точки фокуса линзы. Расположить одно из отверстий в центр расфокусированного пятна.
3.4. Установить экран на расстоянии 50 – 100 см от фокальной плоскости линзы. На экране будет наблюдаться дифракционная картина.
3.5. Передвигая экран, добиться появления в центре дифракционной картины светлого пятна. Для данного положения измерить расстояния от фокальной плоскости линзы до отверстия R1 и от отверстия до экрана L1 . Число открытых зон Френеля k1 определяется из (3) выражением:
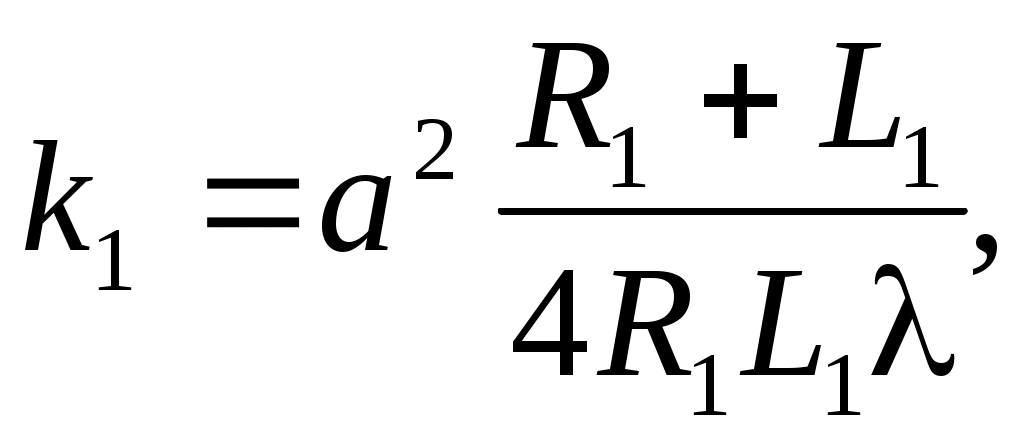 (9) (9)
где a – диаметр отверстия, l – длина волны излучения лазера.
3.6. Плавно перемещая пластинку с отверстием вдоль оси системы, найти ближайшее положение, когда в центре дифракционной картины появится темное пятно. Переход от светлого пятна к темному (или наоборот) соответствует изменению числа открытых зон Френеля на единицу.
3.7. Передвигая пластинку с отверстием дальше, определить общее число таких изменений Dk (желательно 3 – 5). Измерить расстояния R2 и L2 для конечного положения экрана. Для этого положения можно записать:
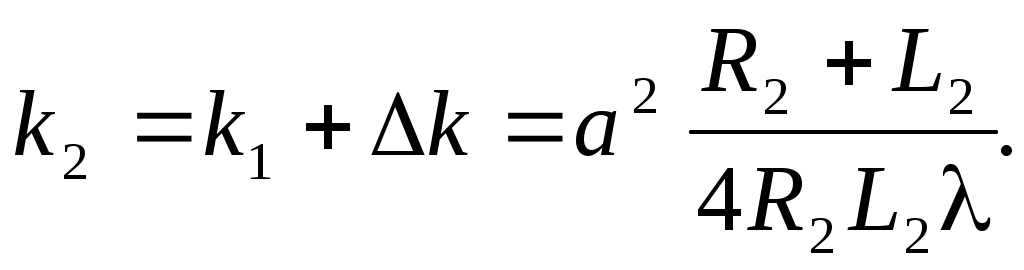 (10) (10)
3.8. По формуле
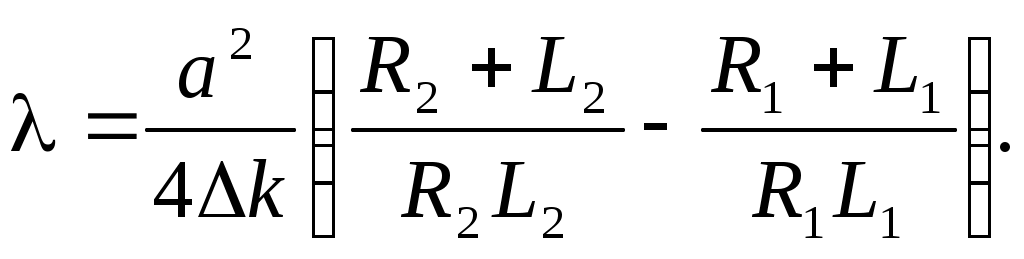 (11) (11)
определить длину волны l излучения лазера.
3.9. Повторить п.п.3.3 – 3.8. для всех отверстий.
3.10. Провести статистическую обработку результатов с доверительной вероятностью 90%. Сравнить полученный результат с истинной длиной волны лазера.
3.11. Установить оптические элементы согласно рис.5, но без зонной пластинки.
3.12. Съюстировать линзы по лазерному лучу. Расположить линзы так, чтобы они образовали телескопическую систему. Фокусы линз при этом совпадают. На выходе такого телескопа должен получиться широкий параллельный пучок света. Проверить параллельность этого пучка: диаметр пучка не должен изменяться с изменением расстояния от телескопа.
3.13. Установить на оптическую скамью между телескопом и экраном зонную пластинку так, чтобы пучок света падал в центр зонной пластинки нормально поверхности.
3.14. Перемещая экран вдоль оптической оси, зафиксировать положение, при котором в центре дифракционной картины наблюдается яркая точка. Измерить расстояние L от пластинки до экрана. Это измерение даст значение главного фокусного расстояния f0 зонной пластинки.
3.15. Передвигая экран, зафиксируйте остальные фокусы fm зонной пластины. Фокусные расстояния fm и главное фокусное расстояние f0 связаны соотношением:
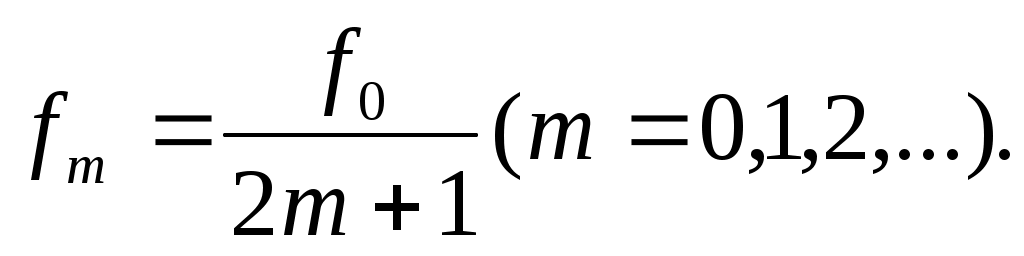 (12) (12)
(В данном эксперименте удается измерить фокусные расстояния лишь при m = 0 и 1).
3.16. Повторите пп.3.14 – 3.15 пять раз. Усредните полученные результаты.
3.17. Сравните экспериментально полученные значения fm и рассчитанные по формуле (12).
4. Контрольные вопросы и задания
Что понимается под дифракцией света? Можно ли отнести явление миража к дифракционному явлению?
Сформулируйте принцип Гюйгенса-Френеля. В чем заключаются допускаемые приближения?
Изложите метод зон Френеля и проведите на его основе анализ полученных в данной лабораторной работе результатов при дифракции световых волн на круглом отверстии.
Освещенность в точке P за круглым отверстием, открывающим одну зону Френеля, примерно в четыре раза больше, чем при полностью открытом волновом фронте. Если увеличить вдвое площадь отверстия, освещенность в точке P уменьшится почти до нуля, несмотря на удвоение светового потока. Как эти факты согласовать с законом сохранения энергии?
Получите выражение для зонной пластинки и докажите ее фокусирующее действие. Увяжите эти результаты с фокусирующим действием линзы.
В чем заключается метод векторных диаграмм в применении к задачам дифракции?
Почему интенсивность в фокусах зонной пластинки максимальна для самого дальнего от пластинки фокуса?
Объясните возникновение светлого пятна в центре тени от круглого диска при освещении последнего светом. В каких условиях можно обнаружить это пятно?
Покажите с помощью векторной диаграммы, что освещенность в центре геометрической тени круглого диска, перекрывающего небольшое число зон Френеля, почти такая же, как и в освещенной области.
Как качественно зависит интенсивность пятна Пуассона от расстояния до непрозрачного экрана?
Во сколько раз интенсивность в главном фокусе зонной пластинки больше, чем в фокусе n-го порядка?
Диск диаметром 5 мм, имеющий неровности порядка 10 мкм, расположен на расстоянии 1 м от точечного монохроматического источника света, излучающего на длине волны 0,5 мкм. Точечный источник находится на перпендикуляре к плоскости диска, проходящем через его центр. Считая, что пятно Пуассона видно лишь до тех пор, пока неровности краев диска перекрывают соответствующую зону Френеля не более чем на 1/4 ее ширины, найти минимальное расстояние, на котором можно видеть пятно Пуассона.
Точечный источник монохроматического света расположен на расстоянии R от круглого отверстия, а экран – с противоположной стороны на расстоянии L. При каких значениях радиуса r отверстия центр наблюдаемых на экране дифракционных колец будет светлым, а при каких – темных?
Точечный монохроматический источник света (l = 0,5 мкм) расположен на расстоянии 0,5 м от плоского экрана с круглым отверстием диаметром 0,5 мм на перпендикуляре к плоскости экрана, проходящей через центр отверстия. На каком расстоянии от отверстия на перпендикуляре расположена точка, имеющая максимум освещенности?
Какова будет интенсивность света I в фокусе зонной пластинки, если закрыть всю пластинку, за исключением верхней половины первой зоны? Интенсивность света без пластинки равна I0.
Какова интенсивность света I в центре дифракционной картины от круглого экрана, если он закрывает всю первую зону? Интенсивность света в отсутствие экрана равна I0.
Монохроматический точечный источник расположен на оси зонной пластинки на расстоянии R от нее. Наиболее яркое изображение источника получается на расстоянии L от пластинки. На каких расстояниях получаются другие изображения источника?
Лабораторная работа
ДИФРАКЦИЯ ФРАУНГОФЕРА
ЦЕЛЬ РАБОТЫ: изучение дифракции Фраунгофера на одной щели, на двух щелях и амплитудной дифракционной решетке.
ПРИНАДЛЕЖНОСТИ: маломощный непрерывный лазер, раздвижная щель типа спектральной щели, пластина с двумя близко расположенными прозрачными щелями, амплитудная дифракционная решетка, экран, линейка, оптическая скамья с набором рейтеров.
1. Теоретическая часть
1.1. Область дифракции Фраунгофера
Явления дифракции принято классифицировать в зависимости от расстояния источника и точки наблюдения (экрана) до препятствия, поставленного на пути распространения света, а также длины волны дифрагирующего излучения. Обычно рассматривают два типа дифракции – Фраунгофера и Френеля. Проведем разграничение этих типов на примере дифракции световой волны на круглом отверстии радиуса R. В оценке этого разграничения основную роль будет играть отношение площади центральной зоны Френеля (см. лабораторную работу «Зоны Френеля») к площади отверстия. Площадь центральной зоны Френеля приближенно можно оценить из формулы, в которой учтено, что расстояние от источника света до отверстия a1 по порядку величины совпадает с расстоянием a2от отверстия до плоскости наблюдения дифракционной картины:
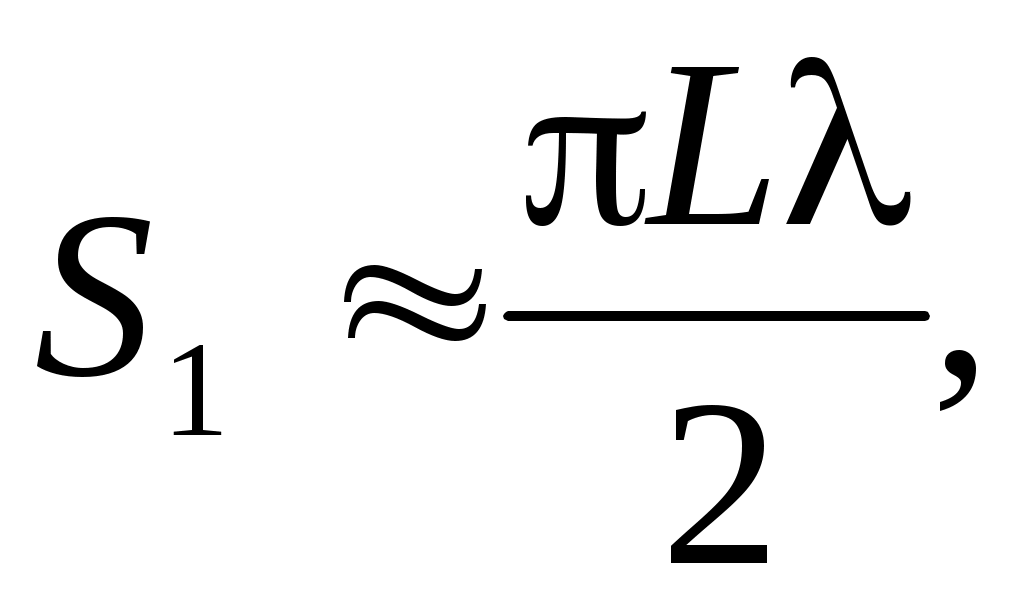 (1) (1)
где L
a1
a2, l – длина волны света.
Площадь отверстия радиуса R равна
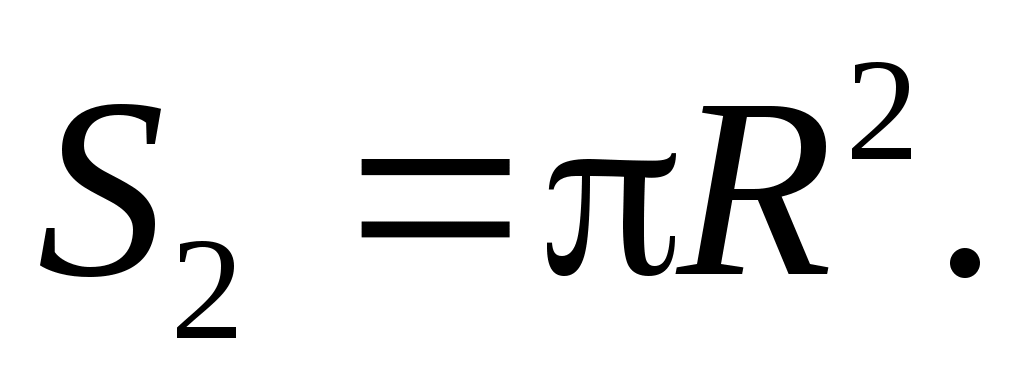 (2) (2)
Введем величину D, равную отношению этих двух площадей и называемую волновым параметром:
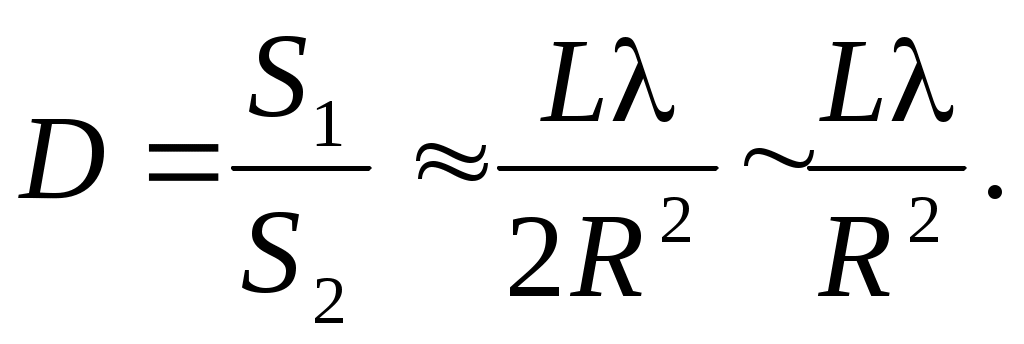 (3) (3)
Волновой параметр играет большую роль в задачах дифракции. Можно выделить три случая:
D << 1. Отверстие имеет размеры много больше размеров центральной зоны Френеля. В этом случае – случае большого отверстия (или очень малых длин волн) – выявить дифракционные, т.е. волновые проявления света достаточно трудно и можно говорить о соблюдении законов геометрической оптики.
D
1. При этом условии дифракционные эффекты начинают играть существенную роль. Например, если отверстие совпадает с центральной зоной Френеля, то интенсивность света в центре дифракционной картины в 4 раза больше интенсивности света в той же точке, создаваемой полностью открытым фронтом. Этот случай соответствует дифракции Френеля.
D >> 1. Размеры препятствия много меньше размеров центральной зоны Френеля. Этот случай наблюдается или при очень больших длинах волн (как правило, это соответствует радиодиапазону), или при большом удалении источника света от препятствия, когда можно считать, что на препятствие падает практически плоская волна. Поэтому этот случай называется дифракцией в параллельных лучах, дифракцией в дальней зоне или чаще дифракцией Фраунгофера.
Именно дифракция Фраунгофера играет основную роль для расчетов большинства оптических приборов. Практически для осуществления дифракции Фраунгофера точечный источник монохроматического света помещают в фокусе собирающей линзы (коллиматора), тогда на препятствие после коллиматора падает практически параллельный пучок света. Или в качестве источника плоской монохроматической волны используют лазер, который имеет малую расходимость пучка, например, гелий-неоновый (He-Ne) лазер. Дифракционная картина наблюдается, в общем случае, на бесконечности или на фокальной плоскости линзы, установленной после препятствия (часто для наблюдения используют зрительную трубу, установленную «на бесконечность»). При достаточно малых размерах препятствий (начиная с
0,1 мм для видимого диапазона дифрагирующих волн) дифракционная картина хорошо наблюдается и на коротких расстояниях (
1 м).
1.2. Дифракция Фраунгофера на одной щели

Рис. 1
Рассмотрим падение плоской монохроматической световой волны на бесконечную щель шириной b (рис.1). Световое поле за щелью найдется по принципу Гюйгенса-Френеля как результат интерференции когерентных вторичных волн, исходящих из различных точек волнового фронта на щели. При таком рассмотрении, по сути предполагается выполнимость граничных условий Кирхгофа для дифракции, согласно которым непрозрачная часть препятствия предполагается неизлучающей вторичные волны.
Участок dx, находящийся на расстоянии x от левого края щели (начала координат), в направлении Z’ излучает плоскую волну с запаздыванием фазы относительно точки О на kx×sinj. Угол j отсчитывается от оси Z – нормали к щели (первоначального направления падающей волны), k – волновое число падающей волны. При записи амплитуды волны учтем, что вся щель в направлении j = 0 посылает излучение с амплитудой E0. Предполагая равномерное распределение амплитуды по щели, получим, что участок dx щели пошлет в направлении Z’ волну dE1с амплитудой E0dx/b :
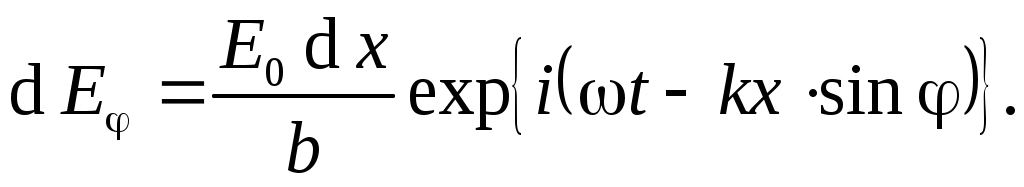 (4) (4)
Отсюда имеем для амплитуды волны от всей щели:
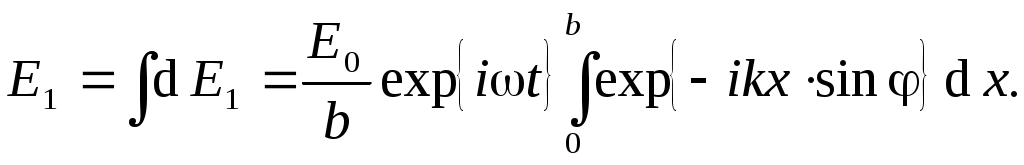 (5) (5)
После несложного интегрирования и перехода от поля к интенсивности, получаем интенсивность дифракционной картины:
 (6) (6)
где I0 = E02 ; I1 = E12 ; 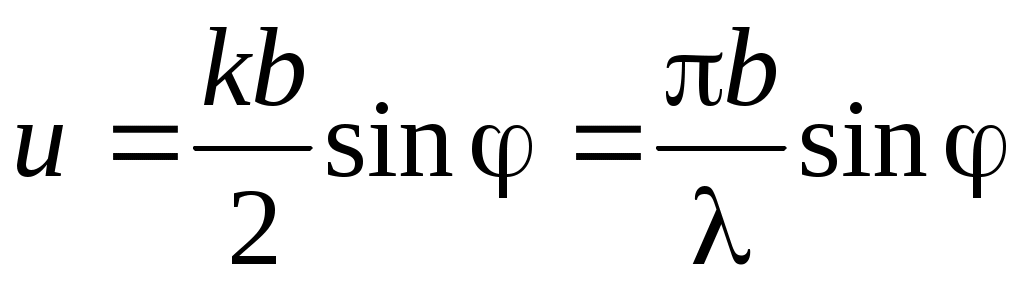 . (7) . (7)
Проанализируем выражение (6).
При j = 0 u =0. Используя соотношение 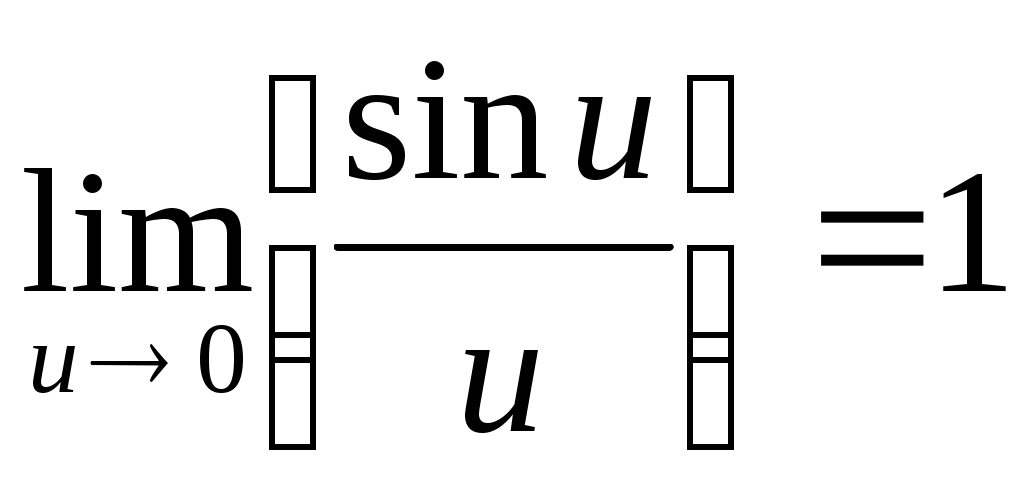 , получаем, что в центре дифракционной картины интенсивность максимальна и равна I0 . , получаем, что в центре дифракционной картины интенсивность максимальна и равна I0 .
При углах j, для которых sinu = 0, а u ¹ 0 интенсивность света обращается в нуль. Тогда условие минимума дифракционной картины на одиночной щели принимает вид:
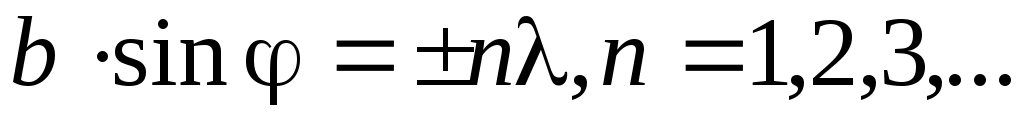 (8) (8)
3. Основная часть потока энергии сосредоточена в пределах изменения угла дифракции j между первыми (n = ±1) симметричными максимумами. График зависимости (6) приведен на рис.2.
4. Чем уже щель, тем шире центральный максимум. Нетрудно заметить, что при b » l центральный максимум расплывается на всю полуплоскость (j » p/2). Дальнейшее уменьшение щели приводит лишь к монотонному уменьшению интенсивности прошедшего света.
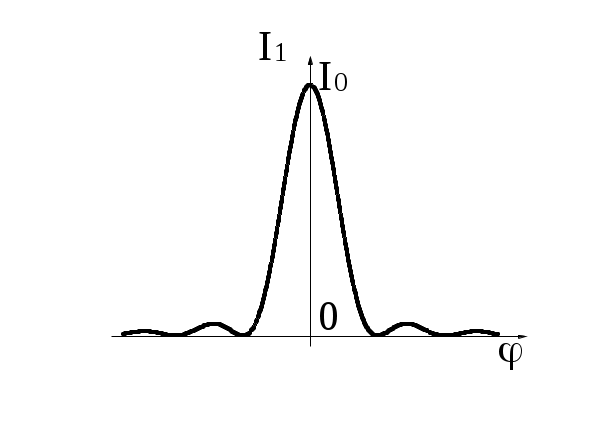
Рис. 2
Изучение картины дифракции дает информацию о ширине щели, если известна длина волны используемого света. Наоборот, зная ширину щели, можно найти длину волны. Таким образом, дифракционная картина от данного объекта имеет характерный вид, позволяющий получать информацию о размерах этого объекта. Отмеченное обстоятельство носит достаточно общий характер и лежит в основе метрологического применения дифракционных явлений.
1.3. Дифракция Фраунгофера на двух одинаковых щелях
В этом случае плоская монохроматическая волна падает нормально на экран с двумя одинаковыми щелями, каждая из которых имеет ширину b, а расстояние между ними – d (рис.3). Расчет дифракционной картины проходит точно так же, как и для случая одной щели. Отличие заключается в том, что выражение для поля от двух щелей, аналогичное (5) состоит из суммы двух интегралов, один из которых имеет пределы [0; b], а другой – [d; d+b]. В итоге интенсивность дифракционной картины примет вид:
 (9) (9)
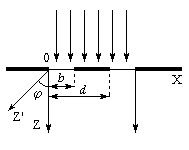
Рис. 3
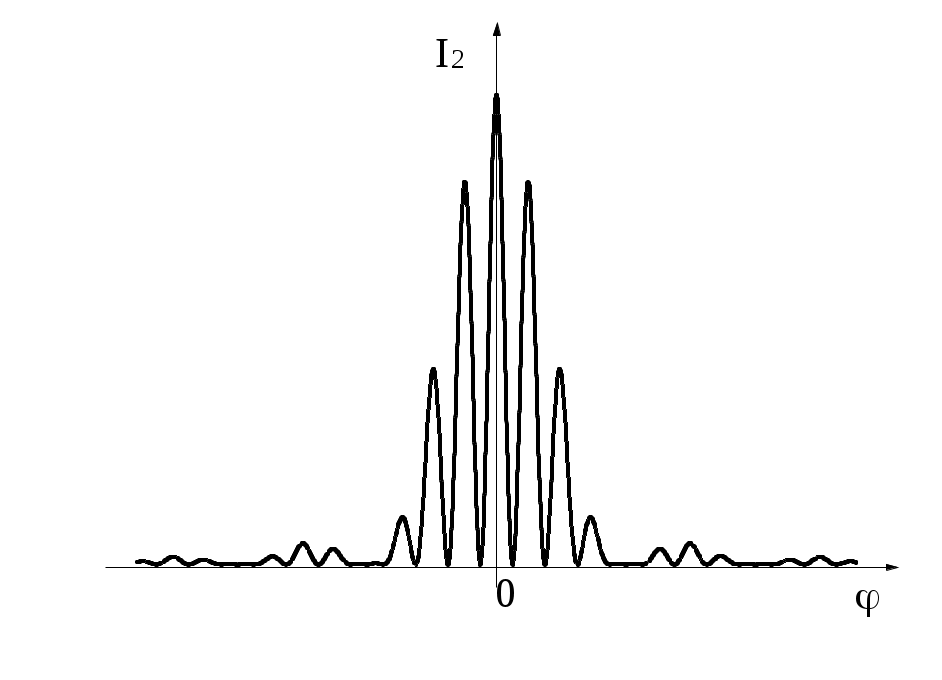 Рис. 4 Рис. 4
где I0– интенсивность света, возникающего в центре дифракционного пятна в том случае, когда открыта только одна из щелей. Из (9) видно, что зависимость распадается на произведение двух сомножителей. Первый из них описывает распределение интенсивности в дифракционной картине Фраунгофера от одной щели. Второй сомножитель обусловлен интерференцией световых волн, приходящих в точку наблюдения от разных щелей. Вид дифракционной картины для данного случая показан на рис.4.
Практический интерес представляют яркие интерференционные полосы (максимумы), расположенные в пределах центрального дифракционного максимума огибающей. Условие этих максимумов вытекает из вида второго сомножителя в (9):
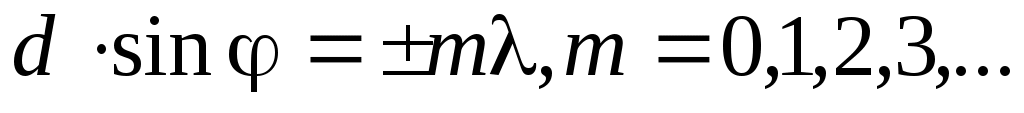 (10) (10)
В пределах центрального максимума огибающей располагается 2d/b таких интерференционных максимумов.
1.4. Дифракция Фраунгофера на дифракционной решетке
Прозрачная (амплитудная) дифракционная решетка представляет собой правильную плоскую структуру из большого количества параллельных щелей с шириной каждой щели b и расстоянием d между соседними щелями. Расстояние d чаще называют периодом или постоянной дифракционной решетки (рис.5). Пусть на эту решетку нормально падает плоская монохроматическая волна. Найдем интенсивность света I в дифракционной картине.
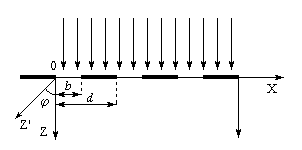
Рис. 5
Методика расчета и система обозначений та же, что и для одиночной щели. От элемента dx какой-то n-й щели в исследуемом направлении распространяется волна вида:
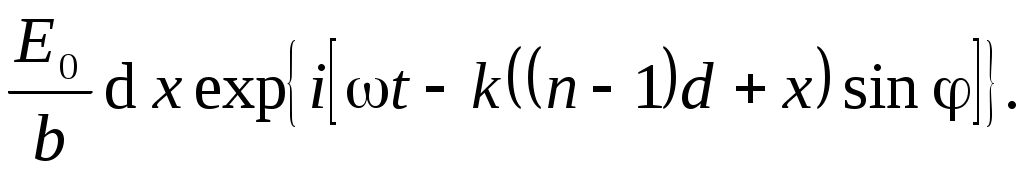 (11) (11)
Вся n-я щель пошлет волну вида:
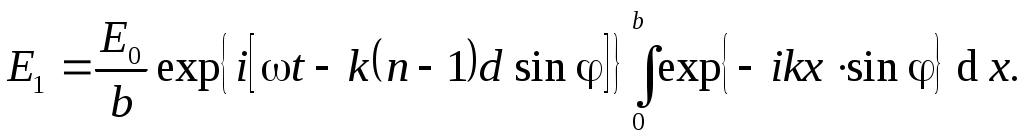 (12) (12)
Для учета действия всех щелей по принципу суперпозиции можно сложить все образовавшиеся напряженности поля:
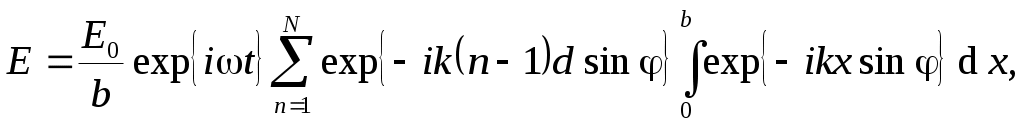 (13) (13)
где N – полное число щелей, участвующих в дифракции.
Множитель с интегралом был посчитан выше для случая одной щели. Он не зависит от n и может быть вынесен за знак суммы. Введем обозначение:
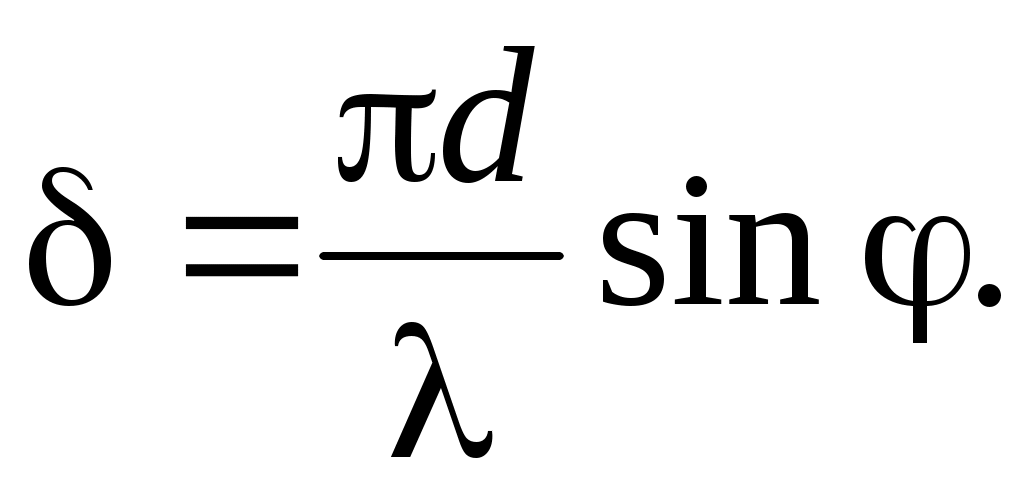 (14) (14)
Сумма в (13) представляет собой сумму N членов геометрической прогрессии. Тогда (13) перепишется в виде
 (15) (15)
Интенсивность света в дифракционной картине получается умножением (15) на комплексно сопряженную величину I=EE* :
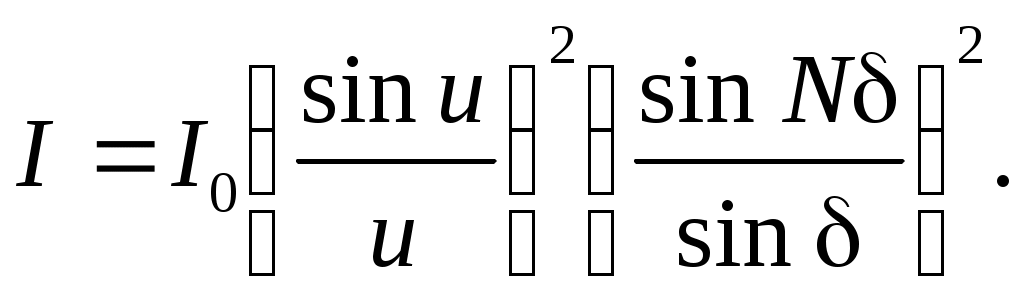 (16) (16)
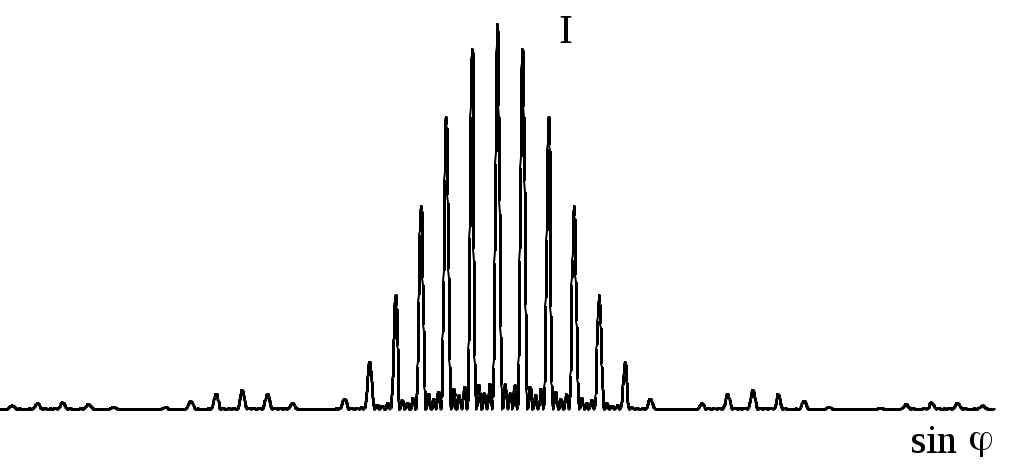
Рис. 6
Рис. 6.
Множитель (sinu/u)2 характеризует распределение интенсивности в результате дифракции плоской волны на каждой щели и является огибающей всей дифракционной картины, а множитель (sinNd/sind)2 учитывает интерференцию между волнами, исходящими от всех щелей. Множитель I0 определяет интенсивность света, излучаемого в направлении j = 0, которая зависит от потока энергии, падающего на решетку света. Вид дифракционной картины показан на рис.6.
Величина dsinj равна разности хода между волнами, испускаемыми двумя эквивалентными точками соседних щелей. Условие главных максимумов для дифракционной решетки определяется формулой (10). А условие (8) определяет положение минимумов огибающей.
2. Описание установки
Лабораторная установка (рис.7) состоит из маломощного непрерывного лазера ((1) – излучатель, (2) – источник питания лазера), линзового телескопа, состоящего из короткофокусной собирающей линзы с фокусным расстоянием f1= 1 см (3) и длиннофокусной собирающей линзы с f2= 14 см (4), стойки (5) с раздвижной щелью, двумя щелями или дифракционной решеткой, рассеивающей линзы (6) с f3= –11 см и экрана (7). Все элементы установлены на оптической скамье (8).
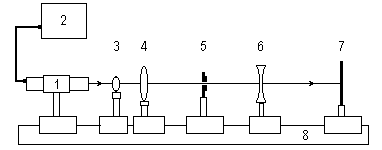
Рис. 7. Схема лабораторной установки
Линзы закреплены в оправах и устанавливаются в рейтеры, которые могут перемещаться вдоль оптической скамьи. Положение всех элементов на скамье определяется с помощью шкалы, прикрепленной к оптической скамье, или линейки. Все оптические детали центрируются, т.е. должны быть установлены так, чтобы их центры лежали на одной высоте, оптические оси линз были параллельны ребру оптической скамьи, плоскость экрана была перпендикулярна оптической оси линз.
3. Порядок выполнения работы
3.1. Определение ширины щели
3.1.1. Установить оптические элементы на оптической скамье (кроме линзы (6)) согласно рис.7 с использованием раздвижной щели. Включить лазер.
3.1.2. Съюстировать линзы телескопа по лазерному лучу. На выходе такого линзового телескопа должен получиться расширенный параллельный пучок света. Проверить параллельность этого пучка: диаметр пучка не должен изменяться с изменением расстояния от телескопа.
3.1.3. Съюстировать раздвижную щель. Пучок света должен идти нормально плоскости щели и симметрично относительно краев щели. Установить отсчет барабана щели на величину 0,1 мм. На экране должна наблюдаться дифракционная картина в виде полос, аналогичная рис. 2.
3.1.4. Измерить расстояние L между щелью и экраном при их наибольшем удалении друг от друга.
3.1.5. Измерить расстояние между одноименными минимумами дифракционной картины. Зная длину волны излучения лазера, расстояние L и порядок минимума, по формуле (8) определить истинную ширину щели. При расчетах учесть малость угла j.
3.1.6. Повторить п. 3.1.5. для минимумов пяти различных порядков.
3.1.7. Провести статистическую обработку результатов с доверительной вероятностью 90%. Сравнить определенное с помощью дифракционного метода значение ширины щели и выставленное по барабану.
3.1.8. Изменяя с помощью барабана щели ее ширину, оценить максимальную ширину, когда еще наблюдаются дифракционные эффекты. Сравнить полученный результат с расчетной оценкой размеров препятствий по формуле (3).
3.2. Определение параметров двойной щели
3.2.1. Установить вместо раздвижной щели стойку с пластинкой с близко расположенными прозрачными щелями. Съюстировать стойку аналогично п.3.1.3. На экране должна наблюдаться дифракционная картина в виде полос, аналогичная рис. 4.
3.2.2. Для получения увеличенной картины установить между щелями и экраном рассеивающую линзу (6) (рис.7). Эта линза создает мнимые изображения щелей на некотором расстоянии L’ от экрана. Мнимые изображения щелей имеют ширину b’ , которая связана с b выражением:
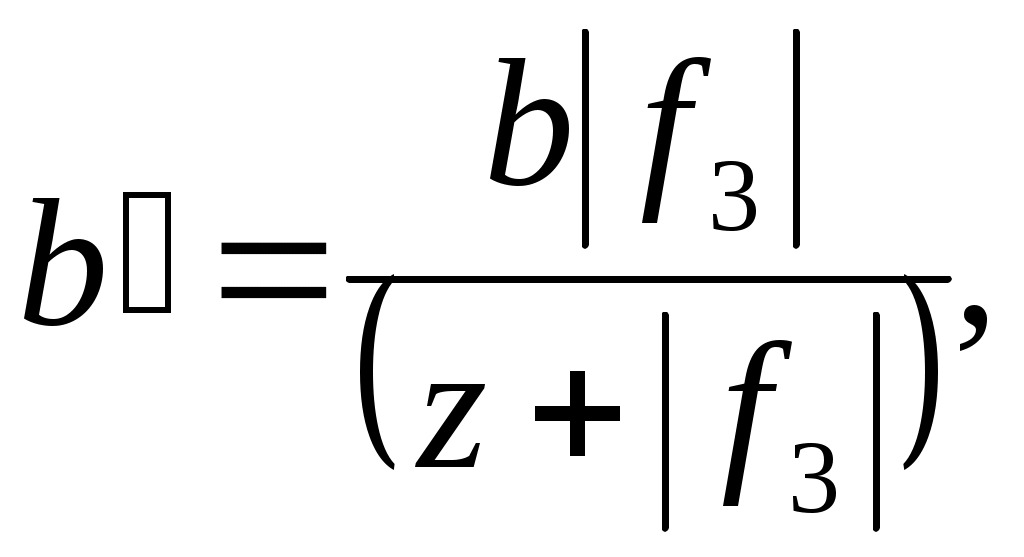 (17) (17)
где z – расстояние от щелей до рассеивающей линзы.
Аналогично для мнимого расстояния между щелями d’ имеем:
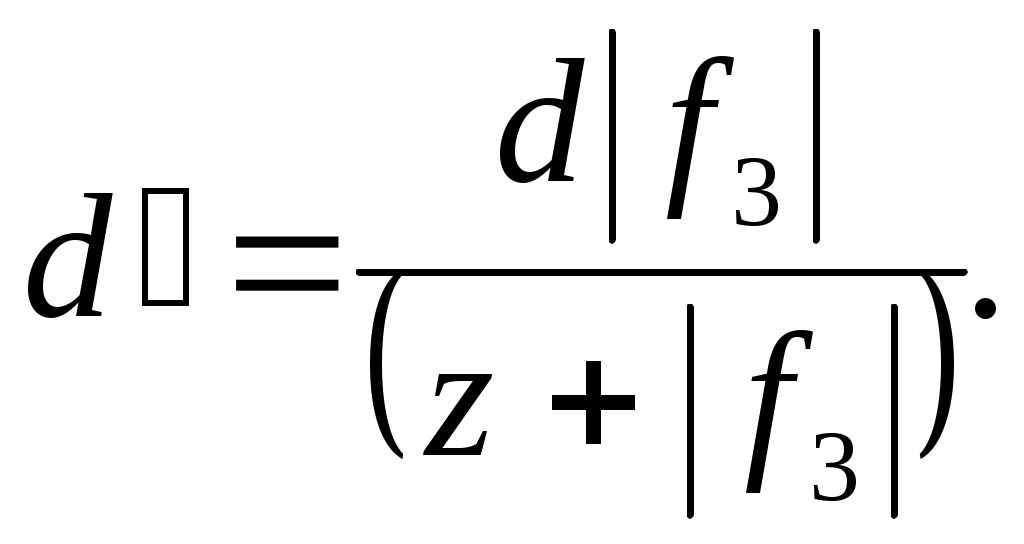 (18) (18)
Расстояние от мнимого изображения щелей до экрана L’ находится по формуле:
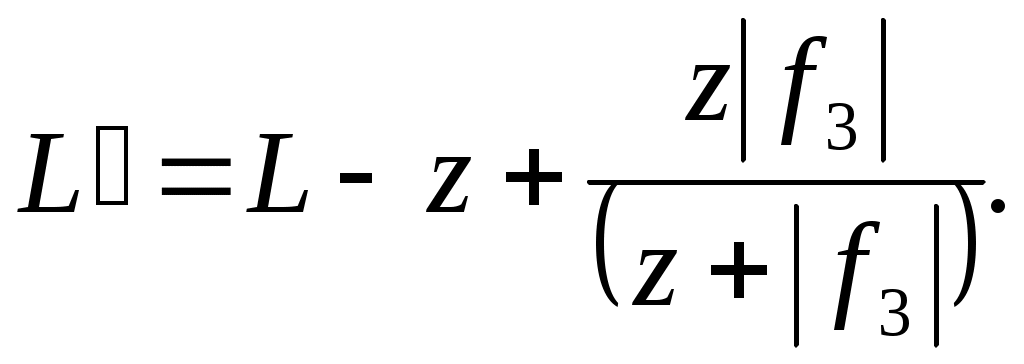 (19) (19)
Максимальный размер картины на экране будет достигаться при
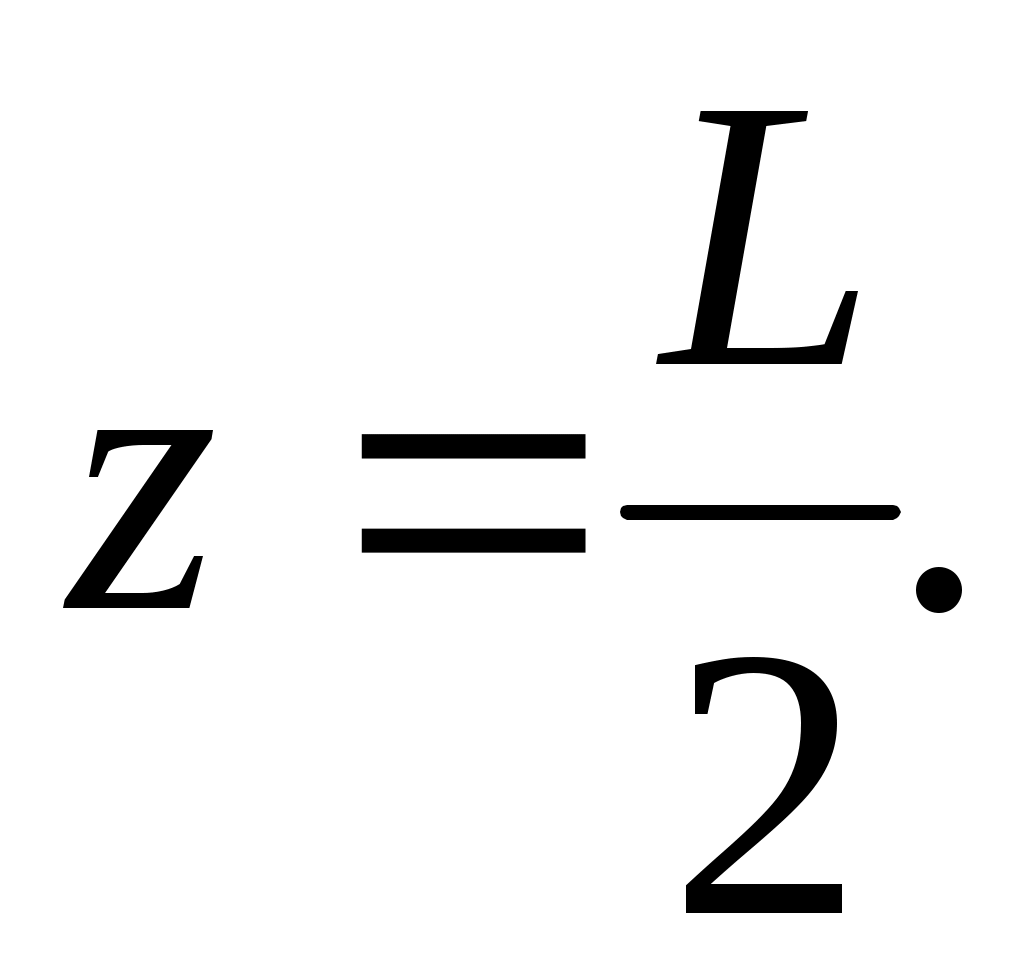 (20) (20)
3.2.3. Используя формулы (8), (10), (17) ¸ (20), и, проведя измерения необходимых расстояний, определить параметры щелей – ширину b и расстояние между ними d. В формулы (8) и (10) необходимо подставлять мнимые значения всех расстояний с учетом малости угла j.
3.2.4. Повторить п.3.2.3 для всех хорошо различимых порядков дифракции. Провести статистическую обработку результатов с доверительной вероятностью 90%.
3.3. Определение постоянной дифракционной решетки
3.3.1. Установить вместо стойки со щелями стойку с дифракционной решеткой. Убрать рассеивающую линзу. Съюстировать стойку аналогично п.3.1.3. Лазерный луч в результате дифракции разделяется на несколько пучков, соответствующих различным дифракционным порядкам, причем луч, соответствующий нулевому порядку, не отклоняется от первоначального направления.
3.3.2. Проведя необходимые измерения линейных расстояний для различных порядков дифракции, по формуле (10) определить постоянную решетки d. Величина sinj находится из формулы:
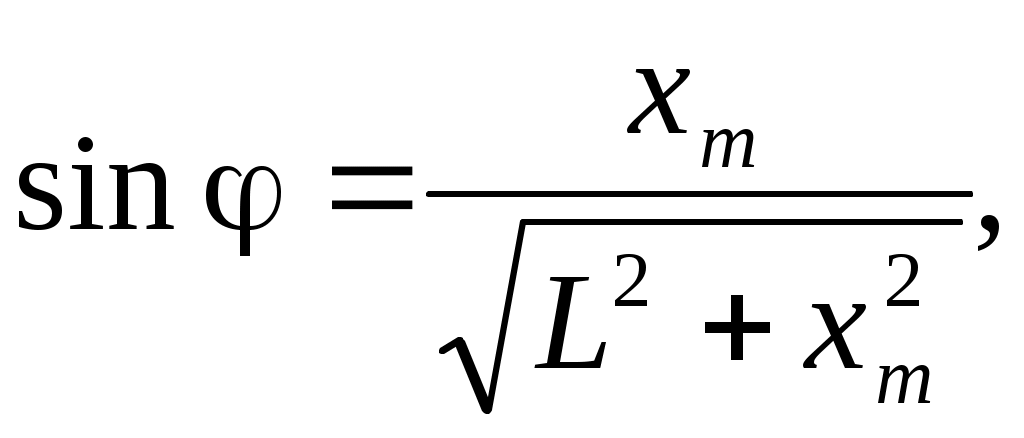 (21) (21)
где xm – расстояние от максимума нулевого порядка до максимума m-го порядка.
3.3.3. Повторить п.3.3.2 для пяти видимых дифракционных порядков. Провести статистическую обработку результатов с доверительной вероятностью 90%.
4. Контрольные вопросы и задания
Каковы должны быть экспериментальные условия для наблюдения дифракции Фраунгофера?
Почему возможно наблюдение картины дифракции Фраунгофера при конечных расстояниях между источником света, препятствиями и экраном?
Как оценить диаметр тонкой проволочки, используя картину дифракции лазерного излучения на этой проволочке?
Каким образом влияют на вид дифракционной картины в случае дифракции на двух щелях ширина отдельной щели и расстояние между ними?
От каких параметров, характеризующих решетку, зависит положение главных максимумов дифракционной картины?
Выведите условия побочных максимумов для дифракционной решетки.
Каким условием определяется наибольший порядок спектра mmax ?
Какую максимальную длину волны можно наблюдать при дифракции на решетке с периодом d ?
Определите характер спектров дифракционной решетки, если ее постоянная равна: а) удвоенной, б) утроенной, в) учетверенной ширине щели.
Как изменится дифракционная картина при наклонном падении плоской монохроматической световой волны на дифракционную решетку?
При каком условии m-й главный максимум для дифракционной решетки с периодом d и шириной щели b обращается в нуль?
Какой максимальный порядок спектра может наблюдаться при дифракции света длины волны l на решетке с периодом d ?
В каких направлениях дифракционная решетка дает минимальную интенсивность света?
Определите минимальное число штрихов в решетке, которая может разрешить натриевый дуплет в спектре первого порядка (l1 = 589,0 нм; l2 = 589,6 нм).

|
|
|
 Скачать 5.21 Mb.
Скачать 5.21 Mb.
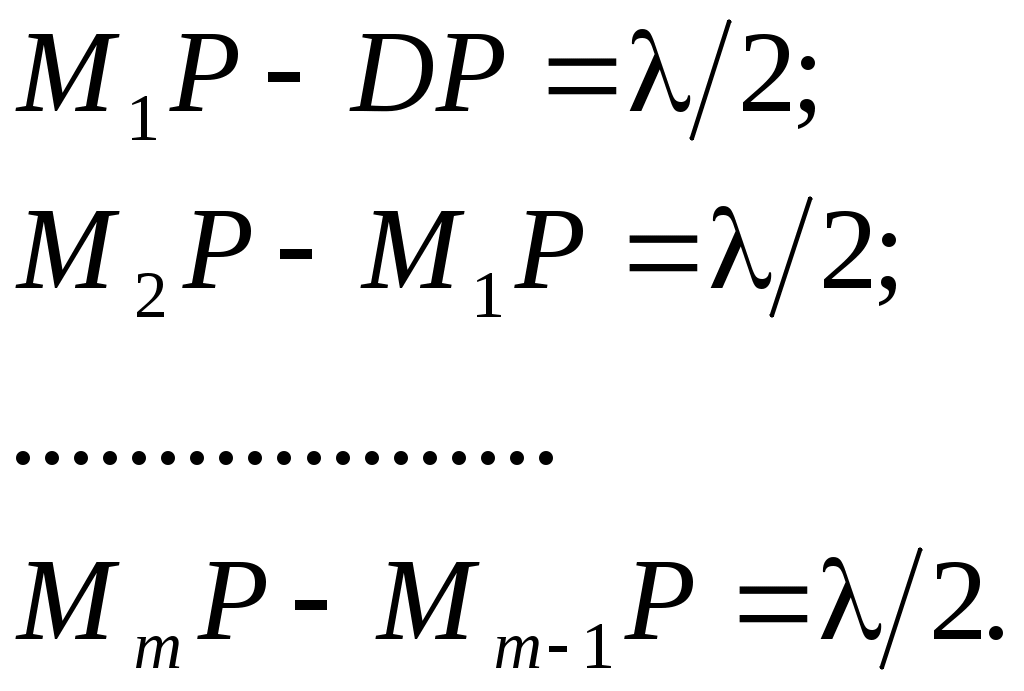 (1)
(1)







 Рис. 4
Рис. 4
 (15)
(15)

