|
|
КСП для 8; 10 класса. Предел функции в точке и на бесконечности
Раздел:
|
|
ФИО педагога
|
Лаган Н.Д.
|
Дата:
|
|
Класс: 10 а
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Определение производной
|
Цели обучения в соответствии
с учебной программой
|
10.4.1.16 - знать определения приращения аргумента и приращения функции;
10.4.1.17 - знать определение производной функции и находить производную функции по определению;
10.4.1.18 - находить производные постоянной функции и степенной функции;
|
Цели урока
|
знает определение производной функции и находить производную функции по определению;
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
|
Организационный момент.
Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей
|
Приготовиться к уроку, настроиться на работу
|
|
|
Середина урока
|
Пусть функция y=f(x)определена в точках x0и x1. Разность x1−x0называютприращением аргумента(при переходе от точки x0к точке x1), а разность f(x1)-f(x0)называютприращением функции.
Определение.Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
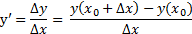
Приращение аргумента обозначают Δx (читают: дельта икс; Δ — прописная буква греческого алфавита "дельта"; соответствующая строчная буква пишется так: δ). Приращение функции обозначают Δy или Δf.
п.40 с.63-65 записать и запомнить формулы.
Пример 1.
Найдем приращение Δx и Δf в точке x0,если f(x)= x2, x0=2 и х=1,9
Решение:
Δx= x1−x0=1,9-2=-0,1
Δf= f(1,9) –f(2)=1,92-22=-0,39
Ответ: Δx=-0,1; Δf =-0,39
Пример 2.
Найдем приращение Δx и Δf в точке x0,если f(x)= x2, x0=2 и х=2,1
Решение:
Δx= x1−x0=2,1-2=0,1
Δf= f(1,9) –f(2)=2,12-22=0,41
Ответ: Δx=0,1; Δf =0,41
|
Выполняют краткий тезисный конспект в тетради
работают с учебником;
|
|
учебник
|
Парная работа
|
Парная работа.
Найти производные следующих функций:
а) y=x5+9x20+1;
б) y=x7-4x16-3;
в) y=x2-15x+6;
Критерии оценивания
-находит производные постоянной и степенной функций
|
работа в парах, взаимопомощь
|
похвала учителя
взаимопроверка
|
|
Индивидуальная работа
|
№ 40.2 (1,2)
|
работают самостоятельно
|
|
|
Рефлекция
|
Рефлексия:
1.С какими новыми понятиями вы сегодня познакомились на уроке?
2.Довольны ли вы результатом? Что удивило или заинтересовало на уроке?
|
Обобщают изученный материал.
Делают вывод.
Оценивают свою работу на уроке(самооценивание)
|
Оценка учителя.
|
|
Домашнее задание
|
п.40,онлайн мектеп
|
Записывают в дневники домашнее задание.
|
|
|
Раздел:
|
|
ФИО педагога
|
Лаган Н.Д.
|
Дата: 25.01.22
|
|
Класс: 10 а
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Теорема Безу, схема Горнера
|
Цели обучения в соответствии
с учебной программой
|
10.2.1.8 - применять теорему Безу и ее следствия при решении задач;
10.2.1.9 - применять различные способы нахождения корней симметрических и однородных многочленов;
10.2.1.10 - применять схему Горнера для нахождения корней многочлена;
|
Цели урока
|
применяет теорему Безу и ее следствия при решении задач;
применяет схему Горнера для нахождения корней многочлена;
находит корни симметрических и однородных многочленов.
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
|
Организационный момент.
Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей
|
Приготовиться к уроку, настроиться на работу
|
|
|
Середина урока
|
Схема Горнера. п.32 с.13
Чтобы выполнить деление многочленов по схеме Горнера нужно:
1) составить таблицу из 2 строк;
2) в верней строке записать коэффициенты делимого: 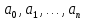 (коэффициенты многочлена (коэффициенты многочлена 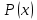 ); );
3) левее старшего коэффициента делимого в нижней строчке записать число 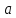 ; ;
4) в нижней строке записать коэффициенты частного  , , 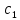 , , 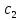 , , , ,  и остаток. и остаток.
Если 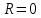 , то многочлен , то многочлен 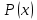 делится на двучлен делится на двучлен 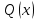 без остатка. без остатка.
Пример. Выполни деление многочленов по схеме Горнера:
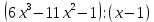 . .
Решение. Составим таблицу:
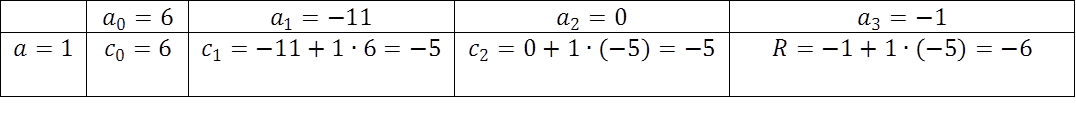
Тогда 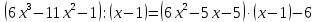 . .
Теорема Безу. Остаток при делении любого многочлена на двучлен 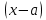 равен значению делимого многочлена при равен значению делимого многочлена при 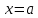 . .
Следствие 1. Многочлен 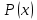 делится на на двучлен делится на на двучлен 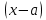 тогда и только тогда, когда число тогда и только тогда, когда число 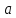 является корнем данного многочлена. является корнем данного многочлена.
Следствие 2. Если 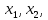 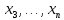 различные корни многочлена различные корни многочлена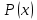 , то , то
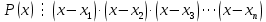 . .
Следствие 3. Числоразличных действительных корней многочлена, отличного от нуля, не более чем его степень.
Пример. Найди остаток от деления многочлена 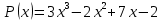 на двучлен на двучлен  , не выполняя деления. , не выполняя деления.
Решение. Согласно теореме Безу, чтобы найти остаток при делении любого многочлена на двучлен, достаточно найти значение  . .
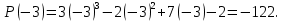
Ответ: 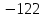 . .
|
Выполняют краткий тезисный конспект в тетради,
работают с учебником;
|
|
учебник
|
Парная работа
|
Парная работа. 1.Разделить 5x4+5x3+x2−11 на x−1, используя схему Горнера.
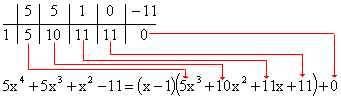
2.Найдите неполное частное, остаток от деления многочлена
Р(х) =х3– 2х2 + 2х– 1 на двучленх–1. Ответ: Q(x) = х2 – х + 1 , R(x) = 0.
Р(х)= 4х5 – 7х4 + 5х3 – 2х + 1 на х-3. Ответ: R(x) = A(3) = 535, Q(x) = 4х4 + 5х3 + 20х2 + 60х +178.
3. Найти остаток от деления многочлена  на двучлен на двучлен 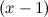 . Ответ:5 . Ответ:5
|
работа в парах, взаимопомощь
|
похвала учителя
взаимопроверка
|
|
Индивидуальная работа
|
№ 32.4 (1)
|
работают самостоятельно
|
|
|
Конец урока
|
Рефлексия:
1.С какими новыми понятиями вы сегодня познакомились на уроке?
2.Довольны ли вы результатом? Что удивило или заинтересовало на уроке?
Домашнее задание №32.4 (1,2 задание из таблицы)
|
Оценивают свою работу на уроке(самооценивание)
|
Оценка учителя.
|
| |
|
|
 Скачать 437.19 Kb.
Скачать 437.19 Kb.