Раздел:
|
10.3А Угол в пространстве. Расстояние в пространстве
|
ФИО педагога
|
Лаган Н.Д.
|
Дата: 28.01.22
|
|
Класс: 10 а
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Векторы в пространстве и действия над ними. Коллинеарные и компланарные векторы
|
Цели обучения в соответствии
с учебной программой
|
10.4.1 - знать определения вектора в пространстве, длины вектора, равных векторов;
10.4.2 - выполнять сложение векторов и умножение вектора на число;
10.4.3 - знать определения коллинеарных и компланарных векторов в пространстве;
|
Цели урока
|
определять равные векторы, коллинеарные векторы, компланарные векторы; находить длины векторов.
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
|
Организационный момент.
Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей
|
Приготовиться к уроку, настроиться на работу
|
|
|
Середина урока
|
Актуализация опорных знаний.
– Вспомните из школьной программы слова, словосочетания, термины, связанные с понятием вектора. (направление, длина вектора, нулевой вектор, коллинеарные, сонаправленные, противоположно направленные, равные, противоположные, сложение, вычитание, умножение на число…)
– Все эти понятия относятся и к векторам в пространстве. Рассмотрим их подробно. Записать все термины тезисно по теме «Векторы в пространстве».
Вектор
Обозначение вектора
Нулевой вектор
Направление нулевого вектора
Длина вектора
Коллинеарные векторы
Сонаправленные векторы
Противоположно направленные векторы
Равенство векторов
Компланарные векторы
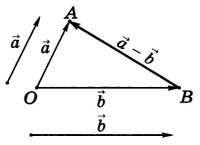
Сложение и вычитание векторов. 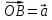 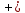 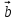 . .

Для того, чтобы найти разность 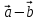 , векторы , векторы  и и 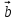 откладывают так, чтобы их начала совпадали. Вектор, у которого начало совпадает с концом вектора откладывают так, чтобы их начала совпадали. Вектор, у которого начало совпадает с концом вектора 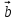 , а конец – с концом вектора , а конец – с концом вектора  , будет искомой разностью векторов. , будет искомой разностью векторов.
|
работают с учебником;
|
|
учебник
|
Парная работа
|
№20.1- 20.4
|
работа в парах, взаимопомощь
|
похвала учителя
взаимопроверка
|
|
Индивидуальная работа
|
№20.6
|
работают самостоятельно
|
|
|
Рефлекция
|
Рефлексия:
1.С какими новыми понятиями вы сегодня познакомились на уроке?
2.Довольны ли вы результатом? Что удивило или заинтересовало на уроке?
|
Обобщают изученный материал.
Делают вывод.
Оценивают свою работу на уроке(самооценивание) о
|
Оценка учителя.
|
|
Домашнее задание
|
|
Записывают в дневники домашнее задание.
|
|
|
1.Найдите площадь прямоугольника, если его периметр равен 74 см, а одна из сторон на 17 см больше другой.
2. В прямоугольнике одна сторона в 4 раза больше другой, а площадь равна 36 см2. Найдите площадь квадрата построенного на меньшей стороне прямоугольника.
3. Площади квадратов, построенных на сторонах прямоугольника равны 64 см2. и 121 см2. Найдите площадь прямоугольника.
4. Стороны параллелограмма 10 см и 12 см, а один из углов равен 300. Найдите площадь параллелограмма.
5.Сторона параллелограмма равна 18 см, а высота, проведённая к ней равна 8 см. Найти периметр параллелограмма, если высота, проведённая к смежной стороне равна 9 см.
6.В параллелограмме:
а) сторона равна 18,5 см, а высота, проведённая к ней – 6 см. Найти площадь параллелограмма;
б) площадь равна 315 см2, а сторона - 9 см. Найти высоту, проведённую к этой стороне.
1.Найдите площадь прямоугольника, если его периметр равен 74 см, а одна из сторон на 17 см больше другой.
2. В прямоугольнике одна сторона в 4 раза больше другой, а площадь равна 36 см2. Найдите площадь квадрата построенного на меньшей стороне прямоугольника.
3. Площади квадратов, построенных на сторонах прямоугольника равны 64 см2. и 121 см2. Найдите площадь прямоугольника.
4. Стороны параллелограмма 10 см и 12 см, а один из углов равен 300. Найдите площадь параллелограмма.
5.Сторона параллелограмма равна 18 см, а высота, проведённая к ней равна 8 см. Найти периметр параллелограмма, если высота, проведённая к смежной стороне равна 9 см.
6.В параллелограмме:
а) сторона равна 18,5 см, а высота, проведённая к ней – 6 см. Найти площадь параллелограмма;
б) площадь равна 315 см2, а сторона - 9 см. Найти высоту, проведённую к этой стороне.
1.Найдите площадь прямоугольника, если его периметр равен 74 см, а одна из сторон на 17 см больше другой.
2. В прямоугольнике одна сторона в 4 раза больше другой, а площадь равна 36 см2. Найдите площадь квадрата построенного на меньшей стороне прямоугольника.
3. Площади квадратов, построенных на сторонах прямоугольника равны 64 см2. и 121 см2. Найдите площадь прямоугольника.
4. Стороны параллелограмма 10 см и 12 см, а один из углов равен 300. Найдите площадь параллелограмма.
5.Сторона параллелограмма равна 18 см, а высота, проведённая к ней равна 8 см. Найти периметр параллелограмма, если высота, проведённая к смежной стороне равна 9 см.
6.В параллелограмме:
а) сторона равна 18,5 см, а высота, проведённая к ней – 6 см. Найти площадь параллелограмма;
б) площадь равна 315 см2, а сторона - 9 см. Найти высоту, проведённую к этой стороне.
1.Найдите площадь прямоугольника, если его периметр равен 74 см, а одна из сторон на 17 см больше другой.
2. В прямоугольнике одна сторона в 4 раза больше другой, а площадь равна 36 см2. Найдите площадь квадрата построенного на меньшей стороне прямоугольника.
3. Площади квадратов, построенных на сторонах прямоугольника равны 64 см2. и 121 см2. Найдите площадь прямоугольника.
4. Стороны параллелограмма 10 см и 12 см, а один из углов равен 300. Найдите площадь параллелограмма.
5.Сторона параллелограмма равна 18 см, а высота, проведённая к ней равна 8 см. Найти периметр параллелограмма, если высота, проведённая к смежной стороне равна 9 см.
6.В параллелограмме:
а) сторона равна 18,5 см, а высота, проведённая к ней – 6 см. Найти площадь параллелограмма;
б) площадь равна 315 см2, а сторона - 9 см. Найти высоту, проведённую к этой стороне.
1.Найдите площадь прямоугольника, если его периметр равен 74 см, а одна из сторон на 17 см больше другой.
2. В прямоугольнике одна сторона в 4 раза больше другой, а площадь равна 36 см2. Найдите площадь квадрата построенного на меньшей стороне прямоугольника.
3. Площади квадратов, построенных на сторонах прямоугольника равны 64 см2. и 121 см2. Найдите площадь прямоугольника.
4. Стороны параллелограмма 10 см и 12 см, а один из углов равен 300. Найдите площадь параллелограмма.
5.Сторона параллелограмма равна 18 см, а высота, проведённая к ней равна 8 см. Найти периметр параллелограмма, если высота, проведённая к смежной стороне равна 9 см.
6.В параллелограмме:
а) сторона равна 18,5 см, а высота, проведённая к ней – 6 см. Найти площадь параллелограмма;
б) площадь равна 315 см2, а сторона - 9 см. Найти высоту, проведённую к этой стороне.
Раздел:
|
|
ФИО педагога
|
Лаган Н.Д.
|
Дата: 2.02.22
|
|
Класс: 8в
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Квадратичная функция и ее график
|
Цели обучения в соответствии
с учебной программой
|
8.4.1.3знать свойства и строить график квадратичной функции вида
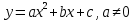 ; ;
|
Цели урока
|
определяют свойства, строят график квадратичной функции вида
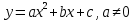 ; ;
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
|
Организационный момент.
Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей
|
Приготовиться к уроку, настроиться на работу
|
|
|
Середина урока
|
Задание на повторение :повторить алгоритм решения неравенства и решить неравенство.
4(x − 1) ≥ 5 + x
4x − 4 ≥ 5 + x
4x − x ≥ 5 + 4
3x ≥ 9 | (:3)
3x (:3) ≥ 9 (:3)
x ≥ 3
 Ответ: x ≥ 3 Ответ: x ≥ 3
Изучение новой темы.
Функцияy=ax2+bx+c– квадратичная. Ее графиком является парабола.
Алгоритм построения графика:
Найти координаты вершины параболы, отметить ее на координатной плоскости.
Провести ось симметрии параболы.
Найти нули функции, если они есть, и построить их на осиOx.
Построить еще несколько точек, принадлежащих параболе.
Провести через построенные точки параболу.
|
Выполняют краткий тезисный конспект в тетради,
работают с учебником;
|
|
учебник
|
Парная работа
|
|
работа в парах, взаимопомощь
|
похвала учителя
взаимопроверка
|
|
Индивидуальная работа
|
|
работают самостоятельно
|
|
|
Конец урока
|
Рефлексия:
1.С какими новыми понятиями вы сегодня познакомились на уроке?
2.Довольны ли вы результатом? Что удивило или заинтересовало на уроке?
Домашнее задание:
|
Оценивают свою работу на уроке(самооценивание)
|
Оценка учителя.
|
|
Раздел:
|
|
ФИО педагога
|
Лаган Н.Д.
|
Дата:
|
|
Класс: 10 а
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Уравнение касательной к графику функции
|
Цели обучения в соответствии
с учебной программой
|
10.4.1.25 - составлять уравнение касательной к графику функции в заданной точке;
|
Цели урока
|
составляют уравнение касательной к графику функции в заданной точке;
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
|
Организационный момент.
Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей
|
Приготовиться к уроку, настроиться на работу
|
|
|
Середина урока
|
Устная работа
Найдите производные:
(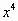 ) ' ( ) ' (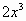 ) ' ( ) ' ( )' )'
Геометрический смысл производнойсостоит в том, что значение производной в точке равно угловому коэффициенту касательной к графику функции в точке.
Механический смысл производной.
Тангенс угла наклона касательной есть величина, показывающая мгновенную скорость изменения функции в данной точке, то есть новая характеристика изучаемого процесса. Эту величину Лейбниц назвалпроизводной, а Ньютон говорил, что производной называется сама мгновеннаяскорость.
Мгновенная скорость в момент времениt вычисляется по формуле
v(t) = x׳(t) = s׳(t) = φ׳(t),
а ускорениеa(t) = v׳(t)= x׳׳(t).
Уравнение касательной к графику функцииf(x)
y = f(x0) + f’(x0)(x-x0)
Пример с.80 и алгоритм
При движении тела по прямой расстояние S(км) от начальной точки меняется по закону S(t) = 8t +t³ . Найдите формулу для вычисления скорости в любой момент времени и вычислите её при t= 2 с.
алгоритм
|
решение
|
Определим, по какому закону изменяется скорость тела, применяя физический смысл производной
|
v(t) = S ׳(t)
v(t) = 8+3t²
|
По условию задачи, время равно 2 секунды, Вычисляя значение полученного выражения при t= 2 с. отвечаем на поставленный вопрос.
|
v(2) = 8+3·2² = 20
|
|
Выполняют краткий тезисный конспект в тетради,
работают с учебником;
|
|
учебник
|
Парная работа
|
№43.7(1,2)
Используем алгоритм
|
работа в парах, взаимопомощь
|
похвала учителя
взаимопроверка
|
|
Индивидуальная работа
|
№ 43.8(1)
|
работают самостоятельно
|
|
|
Конец урока
|
Рефлексия:
1.С какими новыми понятиями вы сегодня познакомились на уроке?
2.Довольны ли вы результатом? Что удивило или заинтересовало на уроке?
Домашнее задание №43.1 (1,2)
|
Оценивают свою работу на уроке(самооценивание)
|
Оценка учителя.
|
|
Раздел:
|
|
ФИО педагога
|
Лаган Н.Д.
|
Дата:
|
|
Класс: 10 а
|
Количество присутствующих:
|
Количество отсутствующих:
|
Тема урока
|
Производная сложной функции
|
Цели обучения в соответствии
с учебной программой
|
10.4.1.22 - находить производную сложной функции;
|
Цели урока
|
знают определение сложной функции и находят её производную;
|
Ход урока
|
Этап урока/ Время
|
Действия педагога
|
Действия ученика
|
Оценивание
|
Ресурсы
|
Начало урока
|
Организационный момент.
Создать благоприятный психологический настрой на работу, подготовка к уроку необходимых принадлежностей
|
Приготовиться к уроку, настроиться на работу
|
|
|
Середина урока
|
Задание на повторение
Устная работа
Найдите производные функций.
а) y = 2x2+ x ;
б) f(x) = 3x2– 7x + 5;
в) f(x) =3х+12;
г) f(x) = 1/2x2;
д) f(x) = (2x – 5)(x + 3).
Сложная функция.
Теорема: Если функция u = g(x) дифференцируема в некоторой точке х0, а функция y=f(u) дифференцируема в точке u0 = g(x0), то сложная функция у=f(g(x)) дифференцируема в данной точке x0.
Алгоритм вычисления производной сложной функции.
определить внутреннюю функцию
найти производную внутренней функции
определить внешнюю функцию
найти производную внешней функции
найти произведение производной внутренней на производную внешней функции.
Учитель у доски: f(x) = (3-5x)5
g(x) = 3-5x
g'(x) = -5
h(g) = g5
h'(g)=5g4
f '(x) = g'(x) ∙ h'(g) = -5 ∙ 5g4 = -5 ∙ 5(3-5x)4 = -25(3-5x)4
Итак, мы выяснили, что такое сложная функция и как вычисляется её производная.
Теперь давайте поучимся находить производные различных сложных функций.
|
Выполняют краткий тезисный конспект в тетради,
работают с учебником;
|
|
учебник
|
Парная работа
|
№45.2
Применяя правило производной сложной функции
|
работа в парах, взаимопомощь
|
похвала учителя
взаимопроверка
|
|
Индивидуальная работа
|
№45.3
|
работают самостоятельно
|
|
|
Конец урока
|
Рефлексия:
1.С какими новыми понятиями вы сегодня познакомились на уроке?
2.Довольны ли вы результатом? Что удивило или заинтересовало на уроке?
Домашнее задание №45.4
|
Оценивают свою работу на уроке(самооценивание)
|
Оценка учителя.
|
| |
 Скачать 437.19 Kb.
Скачать 437.19 Kb.
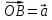
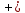
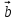 .
.
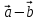 , векторы
, векторы  и
и 
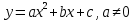 ;
;